用GPS和卫星重力观测估计地表形变的季节性变化*

张良镜 金双根 张腾宇

(1)中国科学院上海天文台，上海 200030 2)中国科学院研究生院，北京100049)

用GPS和卫星重力观测估计地表形变的季节性变化*

张良镜1，2)金双根1)张腾宇1，2)

(1)中国科学院上海天文台，上海 200030 2)中国科学院研究生院，北京100049)

估计和比较GPS和GRACE得到的地表垂直负荷形变，发现全球大部分地区，扣除GRACE地表位移后GPS垂直坐标时间序列均方根(RMS)减小，而且二者周年变化的相位和振幅大部分地区具有较好一致性，反映GPS高程非线性季节性变化主要是由地表质量负荷引起的。然而在某些区域，特别是南极洲、海岸带附近和小岛屿，二者之间存在较大的偏差。分析和讨论两种技术中可能引入的各种误差源及其影响得出，GRACE负荷形变估计影响较小，这与地球物理模型估计的一致性得到了验证，因而剩下偏差是否由GPS本身技术误差所引起，还有待新的高分辨率重力卫星和更多GPS观测和新模型的进一步研究。

GPS;GRACE;高程;地表负荷;季节性变化

1 引言

估计地表负荷形变和研究其变化可了解大气、海洋和陆地水等地表质量运动和相互作用等信息，对全球气候变化和地球动力学研究具有重要作用。目前的大气和海洋模型同化较多实测数据，精度和可靠性相对较高，而水文模型由于缺少实测数据，特别是缺少地下水资料，因而存在较大不确定度，且不同的大气与陆地水文模式输出的陆地水量变化的结果存在较大的差异，较难准确估计陆地水负荷形变和了解其演变过程。GPS的残差时间序列中表现出较为明显的季节性信号，这些信号尤其是周年信号与负荷的影响具有密切的联系。连续的GPS观测可获得地球表面流体总质量引起的非线性运动，但由于其台站分布不均匀，且受GPS本身技术限制，特别是高程方向受电离层延迟、相位中心变化和映射函数等误差影响较大，精度较低。最近卫星重力测量技术，如低低卫-卫跟踪重力恢复与气候试验(GRACE)卫星，能够高精度和高分辨率地确定中长波月尺度的重力场信息，反映地表流体的迁移与重新分布。以往已有大量工作利用重力卫星资料研究诸如陆地水储量变化、极地冰川融化、海平面上升等地球物理变化［1-4］，并且多从负荷质量的角度考虑，例如等效水厚度。而通过时变重力场信息也可获得质量负荷变化引起的垂直形变变化，并能与GPS、VLBI以及SLR等观测技术的观测结果进行比较。两种独立技术GPS和GRACE估计结果的比较还可检核不同技术估计地表负荷的可靠性，特别是理解GPS非线性运动特征。

过去一些学者分析和比较了GPS台站观测坐标与GRACE估算得到的位移变化的时间序列，发现在某些区域，尤其是较大水质量变化区域引起的负荷位移，二者观测结果具有很好的一致［5-7］，然而在欧洲地区等存在较大的偏差［8］。采用重新处理的GPS时间序列比较发现与GRACE时间序列结果较为接近，但GPS本身仍存在较大的误差和不确定性［9］。本文采用ITRF2008提供的最新处理较长时间观测的GPS解析解，其综合了不同分析中心处理结果，并利用最新GRACE时变重力场估计全球地表垂直负荷位移。二者均已扣除几乎相同的潮汐模型影响，如固体潮、极潮与海潮，剩下的地表位移主要由地表流体质量变化引起的。分析和比较两者获取的地表垂直质量负荷位移季节性变化并讨论了可能的误差影响，包括GRACE求解过程可能引入的误差，如高斯平滑等，以及GPS可能的影响因素。

2 观测与计算方法

2.1 GPS观测

GPS坐标时间序列由ITRF2008提供8个IGS分析中心的综合解［10］，其固体潮模型、海洋潮汐模型和极移模型等影响均已扣除，并采用了最新的台站和卫星绝对相位中心改正模型［11］以及新的对流层模型［12］。Altamimi［10］求解了GPS内在精度的径向、东、北3个方向残差时间序列的加权平方根(WRMS)，其中径向的 WRMS为 4.4mm。ITRF2008 IGS测站观测时间跨度从1997-01—2009-05月，约492个台站。本文为了与GRACE数据尽量保持一致，采用了2002年8—12月的数据，并且将噪声较大和数据残缺较多的台站去除掉，最后选取了145个台站(图1)。

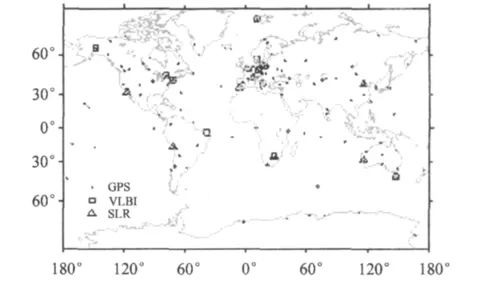
图1 所用的GPS、VLBI以及SLR台站的分布Fig.1 Distribution of used GPS，VLBI and SLR sites

2.2 GRACE估计

GRACE数据采用美国德克萨斯大学空间研究中心提供的高精度Level-2 RL04版本的GRACE重力场60阶的球谐系数(从2002年8月到2008年12月)［13］(UTCSR，Bettadpur 2007)。这里采用的GRACE原始观测数据解算的GSM重力场模型，其中各种潮汐(包括海潮、固体潮、固体极潮)的影响［14］以及非潮汐大气和高频海洋信号均已扣除［13］。为了和GPS观测的整体质量负荷的影响比较，需加上反应大气和海洋质量变化引起的时变重力场的信息的GAC产品系数。它是由欧洲中期天气预报中心(ECMWF)提供的地面大气压以及由海洋环流与潮汐模型(OMCT)提供的海底气压变化得到的球谐系数。GPS观测结果是相对于地球形状中心的参考架的，而GRACE则相对于整个地球质量中心(CM)，为了保持一致，我们使用联合GRACE和地球物理模型得到的重力场1阶系数［15］。此外，由于GRACE对C20不敏感，用SLR得到的结果代替［16］。扣除40个月的平均重力场系数，得到每个月球谐系数的残差值。

根据GRACE月重力场的Stokes系数，依据如下公式，即可求得地球表面GPS台站所处的点的径向位移的变化［9］:

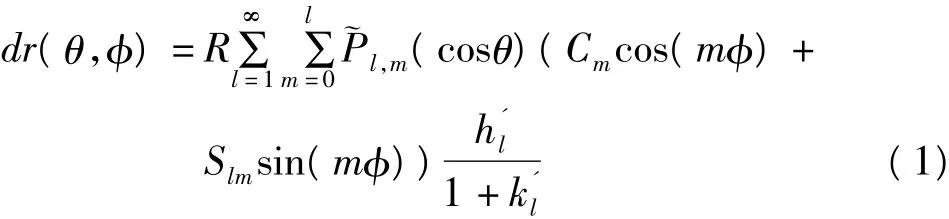
其中，R为地球的平均半径，dr(θ，φ)是地球表面径向位移变化;Pl，m阶数为l、次数为m的归一化的缔合勒让德函数;Clm和Slm为采用的Stokes系数;h'和是l阶的负荷勒夫数。由于GRACE高阶项系数具有较大的误差，我们采用了高斯平滑滤波的方法来减小高阶系数本身误差导致的影响［17，18］。公式(1)转换为:

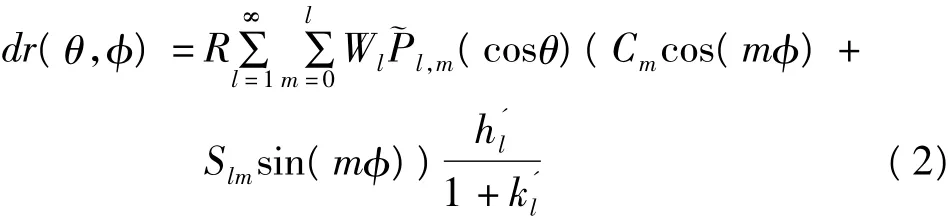
其中Wl表示l阶的Jekeli的高斯平滑函数。这里选取500 km作为折中的平滑半径，既保证最大的降低GRACE噪音，同时对原有数据进行最小的平滑［6］。

2.3 周年信号估计

通过如何计算可以得到GRACE估计负荷垂直位移的时间序列，将其与GPS观测台站的高程坐标一起通过最小二乘拟合，可以得到时间序列的周年信号与半年信号。其信号的振幅与初相位可由下式表示:

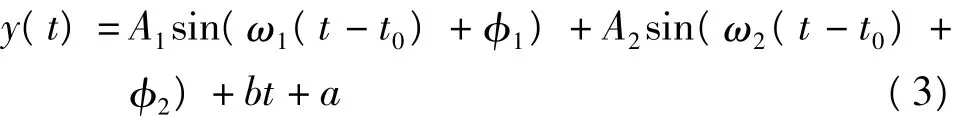
其中，t0的值为2003，ω1、ω2为周年和半年频率。由于半年信号的幅度相对较少，并且受到的影响因素比较复杂，由此本文主要讨论周年变化。

3 结果与分析

3.1 负荷位移比较

利用GRACE重力场球谐系数，结合公式(1)和(2)，可得到GRACE估计的总质量地表负荷垂直位移。扣除GRACE估计的负荷形变可得到GPS高程时间序列的均方根(RMS)。为了量化和比较两者的一致性，我们进一步分析了扣除GRACE前后GPS高程的RMS减少的百分比。其计算公式为:

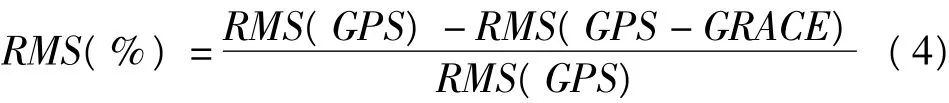
结果发现，对于全球145个台站，其中128个台站的RMS减小了(平均约1.5 mm)。图2显示了扣除GRACE后全球GPS台站RMS较小百分比的分布。另外，还采用皮尔森相关系数求出GRACE和GPS估计的垂直坐标时间序列的相关性，该相关系数是用来反映两个变量线性相关程度的统计量，计算公式为:

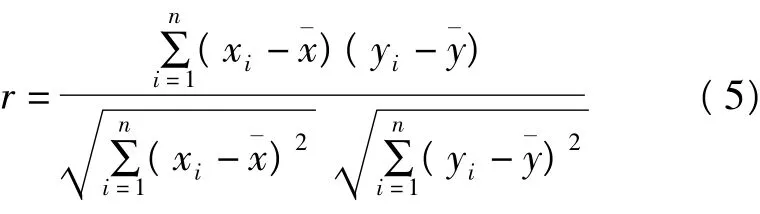
计算结果表明58%的GPS台站与GRACE估计的相关系数大于50%，仅4个台站为负的相关性，分别为MAW1、STJO、TWTF、SEY1。其中3个台站在岛屿上，还有一个在海岸线附近，说明岛屿和海岸线附近的台站处二者之间的相关性明显较差。

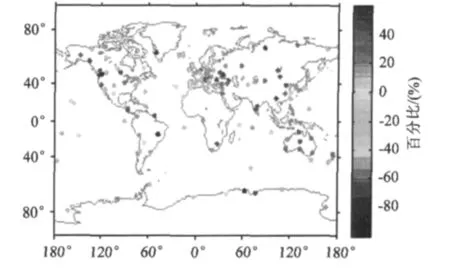
图2 GPS高程均方根(RMS)减小台站的分布Fig.2 Distribution of GPS stations

3.2 季节性变化比较

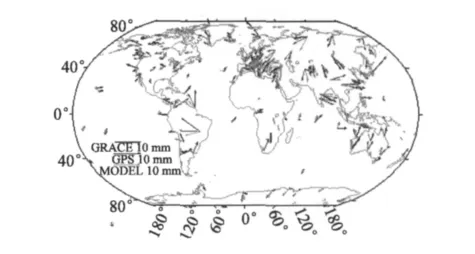
图3 GPS、GRACE和地球物理模型估计的周年变化振幅与初相位比较Fig.3 Comparison among annual variation from GPS，GRACE and geophysical models estimates

GPS与GRACE计算的高程残差时间序列周年信号振幅的RMS分别为4.07 mm和3.23 mm。图3显示了GPS、GRACE及地球物理模型估计得到的地表位移变化周年变化的振幅与初相位图。结果显示在全球的大部分地区，例如亚洲、大洋洲、非洲以及南美洲，GRACE与GPS观测结果吻合得较好，而在南极洲和一些小岛屿存在较大的偏差。本文求得GRACE、GPS的周年信号初相位之差，发现有46%位于-20°～20°之间，83%位于-40°～40°之间。同时为了更精确地比较GRACE和GPS求得的高程残差时间序列周年信号的振幅与初相位，我们还比较了周年信号的同相分量和非同相分量。结果显示同相分量的线性拟合的斜率为0.9278，非同相分量的线性拟合的斜率为1.23，反映二者比较吻合。表1同时显示了GPS、GRACE以及地球物理模型估计的欧洲区域台站处周年信号的振幅与相位。该结果与Van Dam［8］在欧洲区域的GRACE与GPS的比较结果相比发现，GPS与GRACE吻合度提高了很多。从对比结果可以看出，较好的吻合主要归因于GPS数据的改善，这可能与所采用的GPS解处理策略与模型的提高在一定程度上降低了系统差有关。同时比较结果显示，对于大部分台站GPS与GRACE的振幅较为接近，模型的振幅与它们间的差异较大。对于初相位，GRACE与模型较为接近，且在很多区域，模型反而较GRACE与GPS更为吻合。

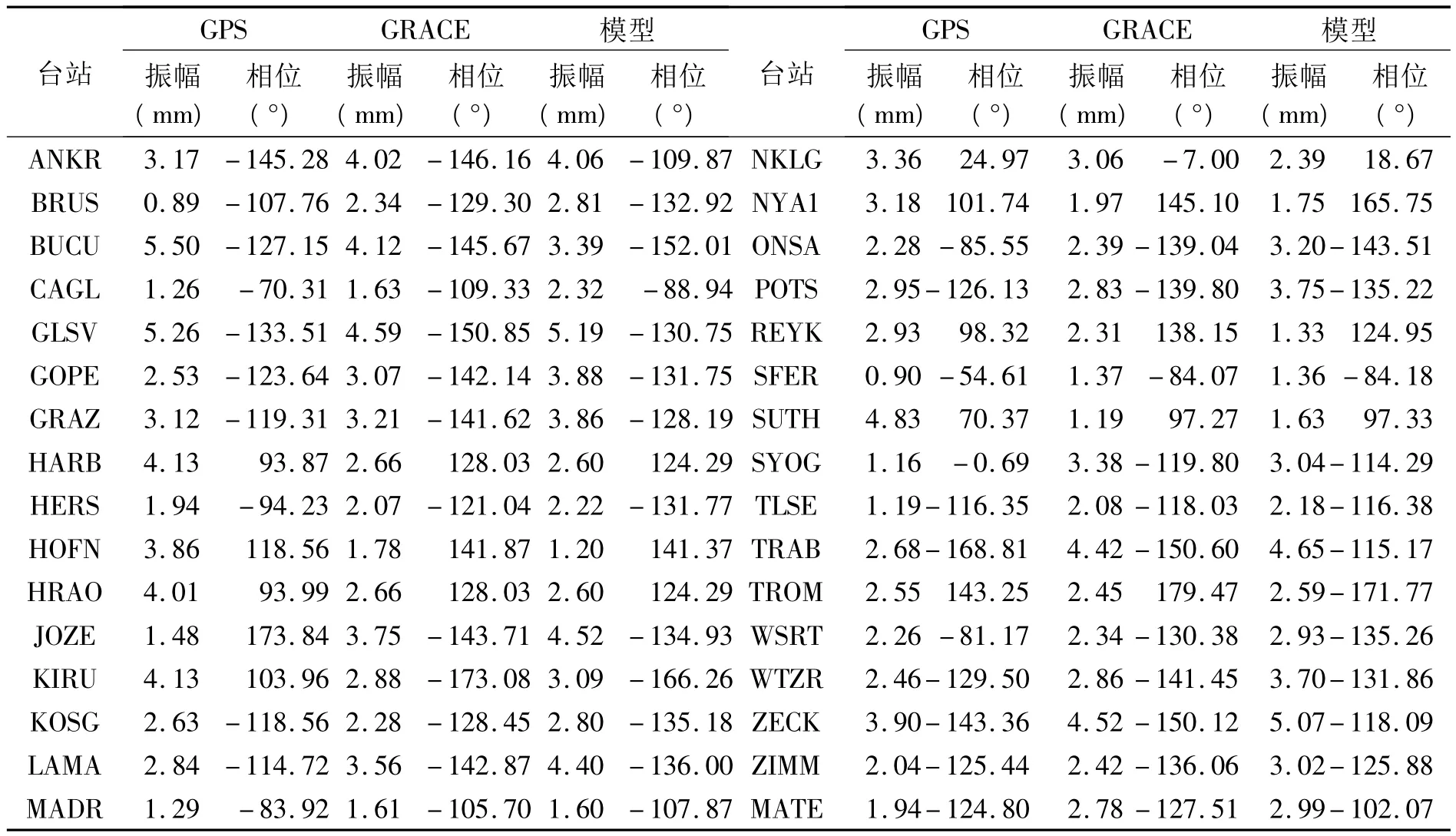
表1 欧洲区域的GPS、GRACE以及模型估计垂直位移周年信号的振幅与相位Tab.1 Amplitude and phase of the annual heights from GPS、GRACE and model in Europe

图4显示了中国及邻区域GPS、GRACE以及地球物理模型得到的地表位移变化周年变化的振幅与初相位分布(箭头的长度代表时间序列周年项的振幅，箭头从向东方向逆时针转过的角度代表周年项的相位)。可以看出周年振幅在不同区域是不一样的，最大振幅出现在KUMN站，也就是恒河-澜沧江流域，幅度约为8.30 mm，最小振幅则位于TWTF台站，为1.18 mm。同时对于大部分台站来说，三者在振幅与初相位上都有较好的吻合。不太好的台站主要有USUD、TWTF、SHAO、PIMO、NTUC。我们详细查看了这些台站的时间序列，发现位于这些台站的GPS的时间序列大部分具有明显的数据缺失。以URUM(87.6°E，43.8°N)和GUAO(87.2°E，43.5°N)为例，这两个台站位置上很接近，但是GUAO站GPS和GRACE估算结果十分接近，而URUM站GPS振幅较小，且在相位上也有一定差别。URUM站的GPS质量明显较GUAO站差，因此GPS数据质量以及其处理策略将会影响其周年变化估计。

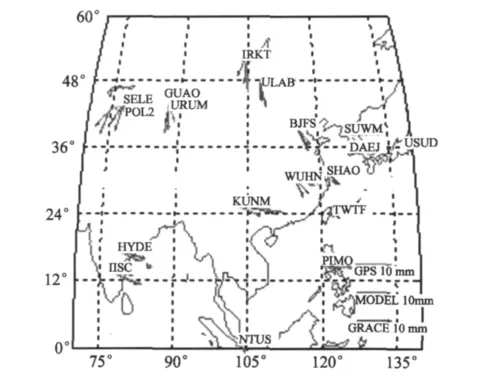
图4 中国及邻区GPS、GRACE和地球物理模型估计的周年变化振幅与相位比较Fig.4 Comparison among annual variations(amplitude，phase)from GPS，GRACE and geophysical models estimates in China and around

4 讨论

4.1 GRACE数据处理中的误差

GRACE观测结果存在较大的条纹和噪音，需要进一步去条纹和平滑，其方法直接影响GRACE估计结果。这里我们还分别计算了以300 km与500 km作为平滑半径平滑不同站点的位移，结果显示两者周年信号的振幅均方根RMS为0.34 mm，750 km导致的变化甚至更少。这个误差远小于GPS与GRACE的估计精度。另外GPS观测的地表坐标是相对于地球形状的中心，而当前GRACE时变重力场信息没有估计一阶项，即重力场系数中一阶项为0。本文采用 Swenson等［15］提供的一阶重力位系数，并分析了一阶项对位移的影响，平均约为0.6 mm，远小于GRACE与GPS的差异，因此这些影响基本上可以忽略。而且Tesmer通过3个处理中心(CSR，JPL以及GFZ)提供的球谐系数分别计算了地表垂直位移，其相互位移时间序列之差的均方差(RMS)为1.2 mm［19］，小于GRACE与GPS的差异。Van Dam［8］研究结果也表明GRACE估计地表位移中的误差远小于GPS与GRACE之间的差异，并推断剩下的差异可能是由GPS数据处理模型及其本身技术问题的影响。

4.2 GPS与GRACE估计垂直位移偏差分析

图3为扣除GRACE和模型估计位移后的GPS残差时间序列周年信号的振幅与初相位，结果显示全球大部分地区，主要包括亚洲，大洋洲，非洲以及南美洲，扣除了GRACE数据以后，GPS周年信号的振幅有了较明显减小。例如图5表示BRAZ站GPS和GRACE估计的负荷垂直位移时间序列，两者非常接近。然而在南极和一些岛屿区域，GPS周年信号的振幅并无明显减小。扣除GRACE以后GPS的残余信号，可能是由于GPS处理中引入的误差，例如对流层和电离层延迟、映射函数、基岩的热胀冷缩、相位中心、多路径效应以及轨道误差等。Kaniuth等［20］与 Jaldehag等［21］发现下雪的时候一些GPS台站的时间序列会出现明显的额外信号，这可能与多路径效应有关。Penna等［22］指出海洋模型中的误差可能引起估算位移时间序列振幅大于1 mm的影响。Tregoning and Herring［7］发现通过全球大气压与温度模型计算的先验天顶延迟可以减小GPS解中的虚假的周年信号。Horwath等［9］发现太阳辐射压和地球反照率模型也可能引起较大的周年信号。另外，对流层模型中映射函数的选用对于位移季节性变化的估计也有较大影响。阎昊明［23］认为温度变化是影响GPS垂直时间序列周年项的一个不可忽视的因素，他发现在中国区域，由GPS台站基岩温度变化引起GPS台站垂直位移变化的周年振幅最大可以达到1 mm。

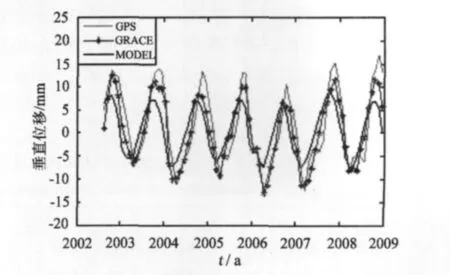
图5 BRAZ站GPS、GRACE以及GLDAS模型估计垂直位移的时间序列Fig.5 Time series of the GPS heights，estimated from GRACE and GLDAS model at BRAZ site

4.3 地球物理模型估计

为了进一步检核GPS和GRACE的估算结果，计算了地球物理模型得到的地表负荷位移。水文模型用的是全球陆地数据同化系统(GLDAS)提供的Noah大陆水文模型的格网数据，其融合了来自地面和卫星的观察数据，提供了最优化近实时的地表状态变量［24］(http://disc.sci.gsfc.nasa.gov/hydrology)。我们将GLDAS提供的的格网点处的积雪数据以及1～4层的土壤水分数据综合起来得到了该处的总的水储存含量，并扣除了2002-08—2008-12的均值得到水储量的变化值。地球表面质量负荷引起的形变位移可以通过格林函数的方法求得［25］。这里为便于和GRACE资料比较，对GLDAS数据进行处理得到每月土壤水的质量变化，并把GLDAS提供的水储存量的变化通过下式转换为60阶的球谐系数:

同时采用与处理GRACE数据同样的方法进行平滑处理进行计算，然后根据公式(2)可以将这些系数转化为地表负荷位移时间序列。

从图3可以看出，地球物理模型得到的周年信号与GRACE较为吻合，尤其是在相位上，这表明地球物理模型在一定程度上验证了GRACE的准确性。但是大部分地区模型估算位移的周年信号振幅略小于GRACE的，这可能由于地球物理模型缺少资料导致，如水文模型GLDAS提供的水储量未包含地下水并且许多地区缺少观测数据。

4.4 SLR和VLBI并置站观测

地表高程变化的时间序列同样可以通过激光测距(SLR)与甚长基线干涉测量(VLBI)技术观测得到，这里我们仍然采用ITRF2008提供的重新处理的综合解。其中VLBI与SLR径向残差时间序列的WRMS分别为7.4 mm与7.9 mm［10］，比GPS的大。由于SLR和VLBI不连续且观测时间有限，因此只有少量的台站数据被采用。本文选取2002—2009年质量较好的10个SLR台站和10个VLBI台站(图1)。我们比较了几个并置站GPS、SLR和VLB观测时间序列与GRACE估计结果。由于SLR以及VLBI数据的质量不是很好，既有数据异常与残缺较为严重，大部分SLR或VLBI与GPS观测结果存在偏差，如观测资料较多3种技术的并置台站WTRZ (图6)。

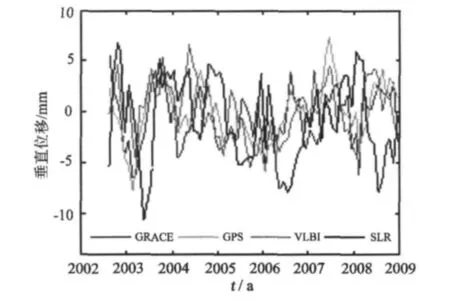
图6 WTZR站GPS、GRACE、SLR以及VLBI估计垂直位移的时间序列Fig.6 Time series of the GPS、GRACE、SLR and VLBI height estimates at WTZR site

5 小结

通过分析和比较GPS与GRACE估计的地表垂直负荷位移时间序列，发现二者周年信号吻合较好。全球大部分地区扣除GRACE垂向位移后，GPS坐标时间序列残差均方差减小，且58%的GPS台站观测与GRACE估计的相关系数大于50%。表明GPS高程非线性季节性变化主要是由GRACE估计的地表质量负荷引起的。但是二者之间仍然存在着一些偏差，这些偏差主要可能由如下几种因素导致:1)两种观测技术本身的差异:GPS得到的是单个台站处的位移，而GRACE反映的是格网区域面上平均结果;2)GRACE低分辨率等问题;3)GPS技术本身和数据处理模型误差，例如对流层和电离层延迟、映射函数、基岩热胀冷缩、相位中心、多路径效应以及轨道误差等影响［26，27］。研究结果表明新的映射函数、天线相位中心改正模型以及轨道模型对GPS时间序列的季节性变化有一定的影响［7，9，28］。虽然GRACE能直接估计全球流体质量负荷位移，较地球物理模型有较大提高，但GRACE只能探测大尺度流体质量变化，不能反映小尺度的流体质量变化，而GPS能监测和反映局部变化或影响，包括小盆地水储存负荷变化。因此需要将来新的重力卫星，以更高分辨率监测地表流体质量，从而得到更高时空分辨率的地表负荷位移。另外需要用更长时间和更多的GPS台站观测结果进一步分析和比较各种技术负荷估计和误差影响。

致谢 感谢美国宇航局(NASA)提供GRACE重力观测数据和IGS提供GPS观测结果。

1 Wahr J，et al.Time-variable gravity from GRACE:first results［J］.Geophys Res Lett.，2004，31:L11501.doi:10.1029/2004 GL019779.

2 Tapley B D，et al.GRACE measurements of mass variability in the Earth system［J］.Science，2004，305:503-505.

3 Velicogna I and Wahr J.Measurements of time-variable gravity show mass loss in Antarctica［J］.Science，2006，311:1 745-1 756.

4 Chambers，et al.Preliminary observations of global ocean mass variations with GRACE［J］.Geophys.Res.Lett.，2004，31(424):L13310.doi:10.1029/2004GL020461.

5 Davis J L，et al.Climate-driven deformation of the solid Earth from GRACE and GPS［J］.Geophys.Res.Lett.，2004，31:L24605.doi:10.1029/2004GLO21435.

6 King M，et al.Choice of optimal averaging radii for temporal GRACE gravity solutions，a comparison with GPS and satellite altimetry［J］.Geophy J Int.，2006，166:1-1.

7 Tregoning P，et al.Detecting hydrologic deformation using GRACE and GPS［J］.Geophys.Res.Lett.，2009，36: L15401.doi:10.1029/2009GL038718.

8 Van Dam T，Wahr J and Lavalle’e D.A comparison of annual vertical crustal displacements from GPS and gravity recovery and climate experiment(GRACE)over Europe［J］.J Geophys Res.，2007，112:B03404.doi:10.1029/ 2006JB00433.

9 Horwath M，et al.Mass variation signals in GRACE products and in crustal deformations from GPS:a comparison［A］.In:Flechtner(eds)System Earth via geodetic-geophysical space techniques，advanced technologies in earth sciences［C］.Springer，Berlin，2010，399-406.

10 Altamimi Z，Collilieux X and Laurent Métivier.ITRF2008: an improved solution of the International Terrestrial Refer-ence Frame［J］.Journal of Geodesy，2011，(05):457-473.doi:10.1007/s00190-011-0444-4，2011.

11 Schmid R，et al.Generation of a consistent absolute phasecenter correction model for GPS receiver and satellite antennas［J］.J Geod.，2007，81:781-798.doi:10.1007/ s00190-007-0148-y.

12 Boehm J，Heinkelmann R and Schuh H.Short note:a global model of pressure and temperature for geodetic applications［J］.J Geod.，2007，81:679-683.doi:10.1007/s00190-007-0135-3.

13 Bettadpur S.CSR level-2 processing standards document for product release04，GRACE［C］.The GRACE project.Center for Space Research，University of Texas at Austin，2007，327-742.

14 Petit G and Luzum B.IERS conventions，IERS technical note 36［R］.Verlagdes bundesamts für Kartographie und Geodäsie，Frankfurtam Main，Germany，2010，http:// tai.bipm.org/iers/conv2010/

15 Swenson S，Chambers D and Wahr J.Estimating geocenter variations from a combination of GRACE and ocean model output［J］.J Geophys Res.，2008，113:B08410.doi:10.1029/2007JB005338.

16 Cheng M and Tapley B D.Variations in the Earth's oblateness during the past 28 years［J］.J Geophys Res.，2004，B9:109.

17 Jekeli C.Alternative methods to smooth the Earth’s gravity field［D］.Department of Geodetic Science and Surveying，Ohio State University，Columbus，Ohio，1981.

18 Wahr J，Molenaar M and Bryan F.Time variability of the Earth’s gravity field:Hydrological and oceanic effects and their possible detection using GRACE［J］.J Geophys Res.，1998，103:30 205-30 229.

19 Tesmer V，et al.Vertical deformations from homogeneously processed GRACE and global GPS long-term series［J］.Journal of Geodesy，2011，85(5):291-310.doi:10.1007/s00190-010-0437-8.

20 Kaniuth K，Stuber K and Vetter S.Sensitivitätvon GPS-höhen bestimmurgen gegen Akkumulationvon Schnec anf der Antenne［J］.AVN.112(8-9):290-295.

21 Jaldehag R T K，et al.Geodesy the suredish permament GPS network:effects of signal scathening on estimates of relative site［J］.J.Geophy.Res.，1996，101(8):1 601-1 604..doi:10.96JB01183

22 Penna N，King M A and Stewart M P.GPS height time series:short peviod origins of spnvious long-penod signals［J］.J Geophys Res.，2007，112:B02402.doi:10.1029/ 2005JB004047

23 阎昊明，等.温度变化对我国GPS台站垂直位移的影响［J］.地球物理学报，2010，53(4):825-832.Doi:10.3969/j.issn.0001-5733.2010.04.007.(Yan Haoming，et al.Thernal effects on vertical diaplacement of GPS stations in China［J］.J Geophy.，2010，53(4):825-832.Doi:10.3969/j.issn.0001-5733.2010.04.007)

24 Rodell M，et al.The global land data assimilation system［J］.Bull Amer Meteor.，2004，85(3):381-394.

25 Farrell W E.Deformation of the Earth by surface loads［J］.Rev Geophys.，1972，10:761-797.

26 Jin S G，et al.Real-time monitoring and prediction of the total ionospheric electron content by means of GPS observations［J］.Chin Astron Astrophys.，2004，28(3):331-337.

27 Jin S G，Wang J and Park P H.An improvement of GPS height estimates:Stochastic modeling［J］.Earth Planets Space，2005，57(4):253-259.

28 Boehm J，et al.The impact of tropospheric mapping functions based on numerical weather models on the determination of geodetic parameters［R］.IAG meeting，Int.Assoc.of Geod.，Cairns，Australia，2005.

SEASONAL VARIATIONS OF EARTH’S SURFACE DEFORMATION ESTIMATED FROM GPS AND SATELLITE GRAVIMETRY

Zhang Liangjing1，2)，Jin Shuanggen1)and Zhang Tengyu1，2)

(1)Shanghai Astronomical Observatory，CAS，Shanghai200030 2)Graduate University of the Chinese Academy of Sciences，Beijing 100049)

We computed and compared the vertical loading deformation from GPS and GRACE and found that at most global sites，the root mean square(RMS)of GPS coordinate time series decreased after removing the GRACE estimates，and the annual variations of the GPS height at most sites also agree well with GRACE or geophysical model estimates in the amplitude and phase.It indicates that the nonlinear seasonal GPS vertical variation is mainly caused by the geophysical loads.However，at some sites，particularly in the Antarctica，some ocean coasts and small peninsulas，large discrepancy has been found between the estimates with the two techniques.We analyzed and discussed the error sources of the discrepancies between GPS and GRACE and their effects，which is proved by a good agreement with geophysical models，and the remaining disagreement may be due to the GPS technical errors.It needs to further investigate using longer and more GPS and GRACE measurements.

GPS;GRACE;height;surface mass loading;seasonal variations

1671-5942(2012)02-0032-07

2011-12-19

国家自然科学基金(11043008，11173050);上海市浦江人才计划项目(11PJ1411500);中国科学院重大方向项目 (KJCX2-EW-T03)

张良镜，女，1987年生，硕士，从事大地测量与负荷形变研究.E-mail:ljzhang@shao.ac.cn

P227

A