地球自转参数短期预报方法及其实现*

严 凤 姚宜斌

(武汉大学测绘学院，武汉 430079)

地球自转参数短期预报方法及其实现*

严 凤 姚宜斌

(武汉大学测绘学院，武汉 430079)

根据极移及日长变化的特性，采用LS与AR模型相结合的方法，建立了适合地球自转参数(ERP)的预报模型。为减少相邻残差存在的强相关性，先对残差序列进行差分预处理，然后利用AR模型进行ERP的预报。对ERP进行了1—10天的短期预报，其预报精度接近国际最好水平。

地球自转参数;三角多项式模型;自回归模型;预报精度;平稳性检验

1 引言

地球自转参数是指由极移、日长变化以及岁差和章动构成的描述地球自转变化的参数，简称为ERP。ERP表达了地固参考系相对于瞬时天球参考系的运动，是实现天球坐标系与地球坐标系相互转换的必要参数。极移分量表示天球历书轴在地球参考系中的运动。世界时与协调时之差或者日长变化则反映了地球自转的不均匀性。地球定向参数包含有丰富的地球动力学信息，而且还是导航与卫星精密定轨中必需的参数［1］，对其进行实时高精度的预报具有重要的科学意义和应用价值。

近几十年来，随着甚长基线干涉测量、人卫激光测距和全球定位系统等现代测量技术的飞速发展，极大地推动了地球自转变化的研究。然而，由于测量模型和资料处理的复杂性，目前VLBI和SLR等技术获取的ERP参数往往需要延迟2～5天，难以满足导航与卫星精密定轨对ERP参数的时效性需求。因此，寻求高精度ERP预报方法成为一项值得深入研究的课题。目前国际上常用预报方法有最小二乘外推法、协方差法、自回归移动平均法、神经网络法、小波分析、卡尔曼滤波等方法，其预报精度已经达到一定水平。国内对ERP参数进行预报起步较晚，但随着探月工程以及北斗二代卫星导航系统等空间计划的逐步拓展，提高ERP参数预报的精度和时效性已变得十分迫切，目前多家科研机构对此展开了研究。1977年汤家豪教授［2］在AR模型基础上首次提出门限序列自回归模型;2007年王琪洁将大气角动量的影响引入地球自转参数预报中，建立了基于神经网络技术的地球自转变化预报;2008年杨元喜等人［3］提出为了带多适应因子的自适应抗差滤波的动态数据预报方法，有效改善了动态预报精度;2010年许雪晴［4］等人比较LS+AR模型和人工神经网络模型的预报精度，发现AR模型在短期的预报中精度较高，而ANN模型则在中长期预报中有优势。为了研究不同技术和方法对ERP预报精度的影响，2005年10月—2008年2月，国际上举行了一次大型的地球定向参数预报竞赛。这次比赛总共由13组来自不同国家及不同学院的专家参与，经过两年多预报与比较，发现采用LS+AR模型对ERP参数进行短期预报的精度很高。因此本文采用LS+AR模型对地球自转参数进行短期预报，并与EOP PCC的结果进行比较，以验证预报模型的有效性。

2 LS+AR模型

2.1 LS模型

地球自转参数刻画了极移、日长变化、岁差、章动等自然现象的变化，这些变化包括周期性、趋势性等复杂过程，时间序列中主要的部分是周期项和趋势项，本文采用三角多项式模型，并用最小二乘方法来拟合这两项。极移参数计算公式为:

式中a、b为趋势项的拟合系数，c、d为周期项的拟合系数，P1、P2分别为 Chandler项和周年项的周期［5］，ω1、ω2分别为Chandler项和周年项的初始相位。当方程个数大于未知数个数时，可根据最小二乘原理求解参数。

UT1-UTC、Δlod计算公式为:

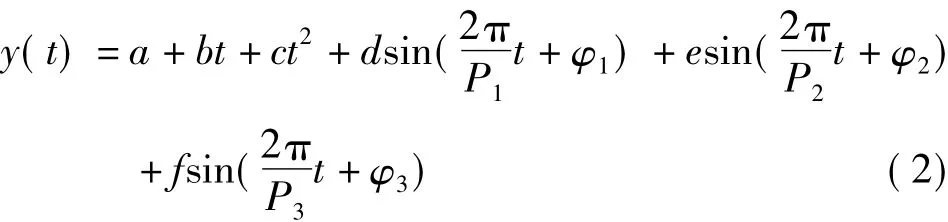
式中:a、b、c为趋势项的拟合系数，d、e、f为周期项的拟合系数，P1、P2、P3分别为Chandler项、周年项和半周年项的周期［6］，φ1、φ2、φ3为这3个周期项的初始相位。

2.2 AR模型

1)预报模型

剔除周期项和趋势项后的残差序列，没有明显的规律特征。经分析，发现该时间序列的后一项与前几项具有相关性，根据这一特点采用自回归(AR)模型来拟合残差序列。自回归模型就是根据变量自身过去的规律来建立预测模型，在动态数据处理中存在广泛的应用。本文采用的自回归模型为:

式中:xt为模型变量;b1，b2，…，bp为模型的回归系数;εt为模型的随机误差;p为模型阶数［7］。

自回归模型是时间序列分析的主要模型之一。在建立自回归模型时，难点在于模型阶数的确定，而这个问题可以利用Matlab高阶统计量工具箱中的函数来解决。确定阶数后，即可用最小二乘方法估计出模型参数。Matlab高阶统计工具箱也提供了相关函数求解模型参数，计算十分简便。

2)外推预报

当回归系数b1，b2，…，bp确定时，可根据方程进行预报。

第一步预报值为:

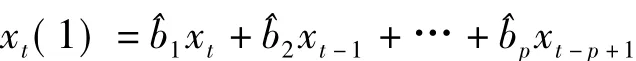
第二步预报值为:

一般地，第l步预报值为:

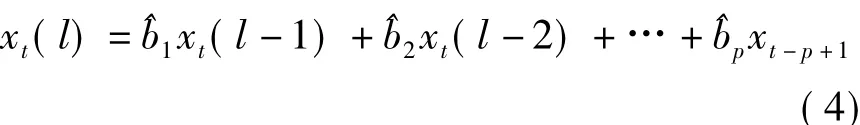
每一个基础时间序列确定一个模型阶数，然后根据模型阶数求出回归系数，再用公式(4)即可进行预报。

2.3 地球自转参数的预报

极移参数预报流程如图1，UT1-UTC的预报流程如图2。

从www.iers.org下载eopc04.62-now文件，抽取极移参数序列、UT1-UTC序列和Δlod序列(图3)，采用从1995年至今的数据进行建模分析。

3 差分处理

图1 极移参数的预报流程Fig.1 Prediction process of polar motion parameters

AR模型要求建模的时间序列是平稳随机序列，即满足平稳、正态、零均值的条件［8］。剔除了周期项和趋势项影响的残差序列，其平稳性还不能满足平稳随机序列的条件。本文提出先对残差序列进行一次差分，再对差分后的残差序列建立AR模型的处理方法。一次差分后的残差序列平稳性大大增强，以极移数据为例，首先利用时间序列的散点图来判断残差序列以及差分后残差序列的平稳性(图4)，可以看出，差分前时间序列都绕其均值上下波动，但差分后的时间序列波动更趋于平稳，更接近零均值。

计算以250天作为子时间序列的极移参数的残差和差分残差的均值统计量以及方差统计量，结果如图5、6。从图5、6可以看出差分后时间序列的均值统计量及方差统计量更接近零，并且每段子时间序列的均值统计量及方差统计量基本不变，说明差分后的时间序列平稳性更强。

极移参数以6年观测数据为基础时间序列，采用对残差序列进行差分处理和不做差分处理两种方案分别进行解算，图7为两种方案解算精度的比较，从图7可以看出进行一次差分处理后，大大提高了预报精度。

Δlod可以与UT1-UTC相互转换，UT1-UTC去掉秒跳后，再作差分，结果的相反数即为Δlod。因此，对Δlod的预报可以转换为对UT1-UTC的预报，再将UT1-UTC的预报值换算为Δlod的值即可。

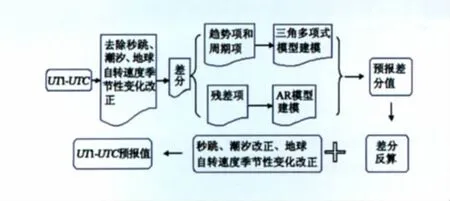
图2 UT1-UTC的预报流程Fig.2 Flow chart of UT1-UTC prediction

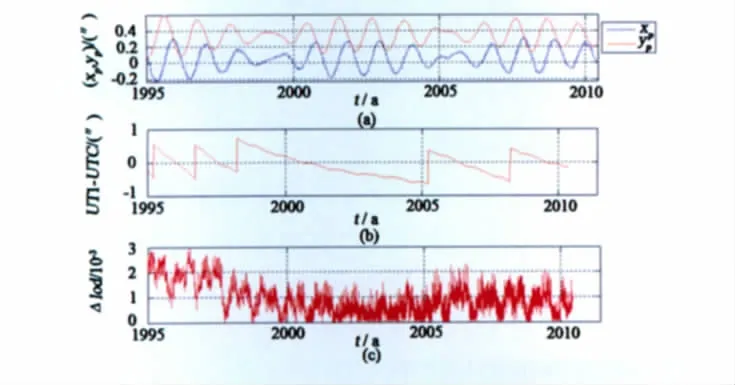
图3 极移参数、UT1-UTC、Δlod基础序列Fig.3 Basic sequences of polar motion parameters、UT1-UTC and Δlod

4 精度检验及结果分析

4.1 精度检验

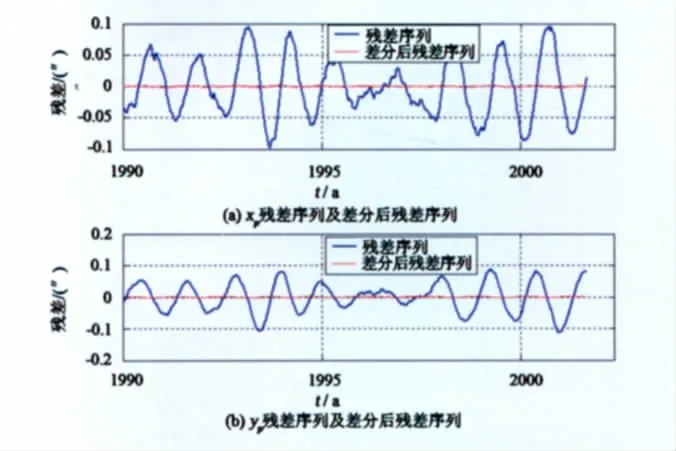
图4 极移参数的残差序列和差分后残差序列Fig.4 Residual sequences of the polar motion parameters before and after the difference

图5 残差序列和差分后残差序列的均值统计量Fig.5 Mean statistics of residual sequences before and after the difference

图6 残差序列和差分后残差序列的方差统计量Fig.6 Variance statistics of residual sequences before and after the difference

为与国际结果进行比较，用预报误差绝对值的平均值(MAE)来评定预报精度，计算式为:

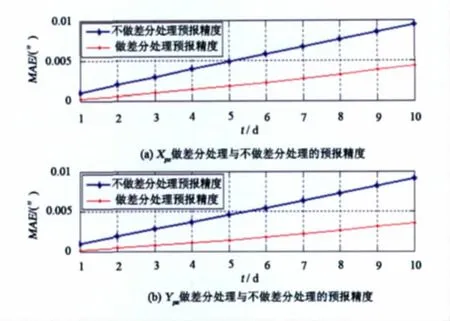
图7 做差分与不做差分预报精度比较Fig.7 Comparison of prediction accuracy between doing and not doing the difference

式中，εi，n是预报值与它在IERS C04中相应值的差值，N为预报次数，I为预报长度。

本文采用与EOP PCC相同的预报间隔和期数，并预报相同时间点的ERP参数。EOP PCC从2005年10月1日起开始预报，每隔7天预报10天的值，总共预报了126期，取预报误差绝对值的平均值作为预报精度(图8(a)［9］)。本文分别采用2005年10月1日前3年、前6年、前9年的数据作为基础序列，建立预报模型，其预报精度如图8(b)。图8反映了本文方法与EOP PCC所用方法的精度比较，其具体分析见表1。

表1 ERP绝对误差(MAE)比较Tab.1 Comparison between ERP mean absolute prediction error

由表1可以看出Xp、Yp方向1～5天的预报精度高于EOP PCC绝大部分预报方法，6～10天预报精度达到EOP PCC领先水平。UT1-UTC 1～10天预报精度均达到EOP PCC领先水平。对于Δlod的预报，EOP PCC中大部分方法的预报精度都不高，精度较高的预报方法1～10天的精度为0.13～0.38 ms/day;本文直接由UT1-UTC的预报结果转换而来的Δlod，其预报精度也相当高，1～10天的预报精度为0.17～0.25 ms/day。综上可见，本文采用三角多项式模型与自回归模型相结合的方法，其预报精度已经达到国际领先水平。

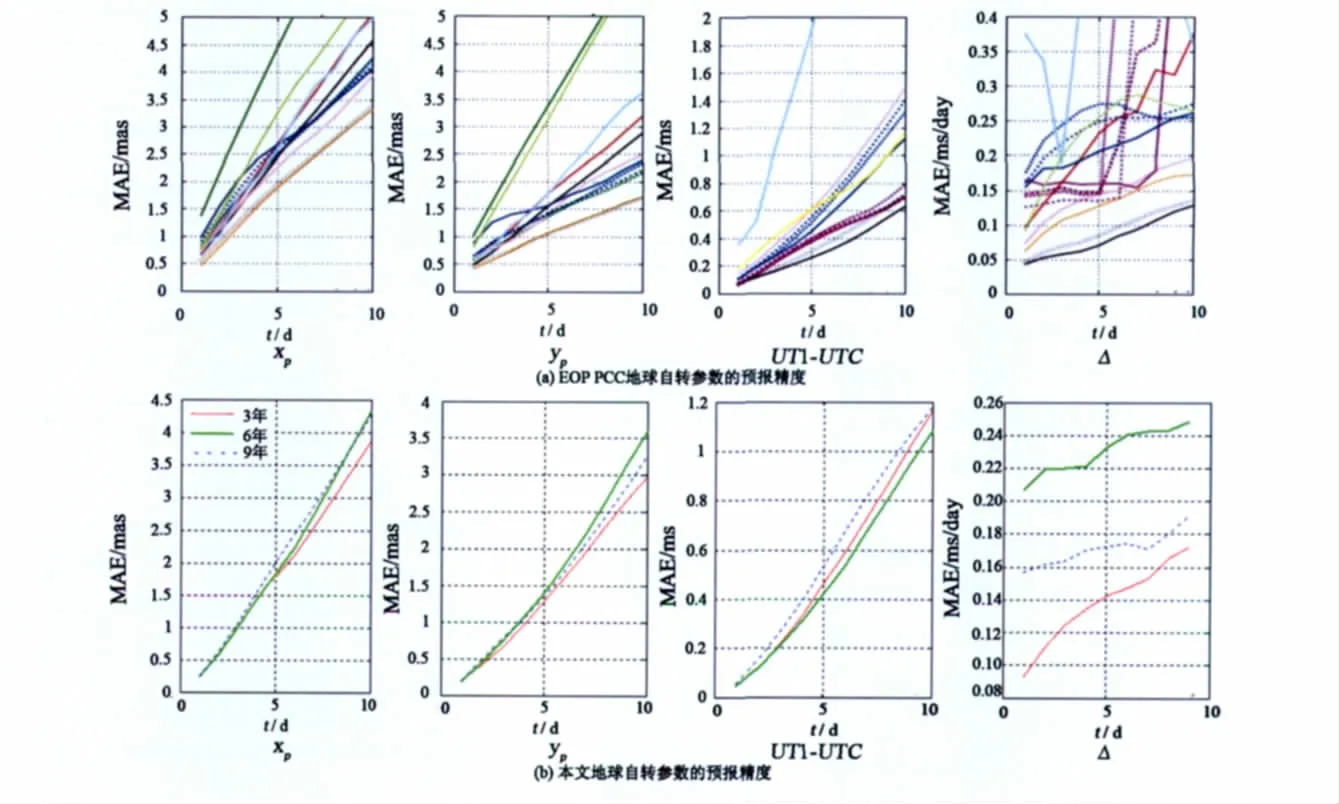
图8 ERP预报精度Fig.8 ERP prediction accuracy

4.2 基础序列长度对预报精度的影响

从上一节可以看出，不同长度的基础序列其预报结果是不一样的。目前，国内外对ERP的预报绝大多数没有考虑基础序列长度对ERP预报精度的影响。本文分别以3年、6年、9年、12年作为基础序列长度对地球自转参数进行预报，寻找基础序列长度与ERP预报精度的联系(图9)。图9中反映，基础序列长度越长，其预报精度反而越差。这主要是因为相邻数据之间具有明显的相关性，而随着时间间隔的增加，相关性逐渐下降。同时ERP基础序列过长的话，其数据的精度不一致，从而影响预报精度。因此，在建立预报模型时，基础序列长度不宜太长，这样一方面可以保证基础序列精度的一致，提高预报精度;另一方面，有效缩短了预报时间。另外，6年接近Chandler周期与周年周期的最小公倍数［9］，选取6年作为基础序列长度，更能体现地球自转参数的周期特征。

图9 3、6、9、12年的预报精度Fig.9 Prediction accuracy of 3，6，9 and 12 years

5 结语

本文采用LS+AR模型对地球自转参数进行预报，并与EOP PCC的结果进行比较，以验证预报模型的有效性。提出先对残差序列进行一次差分处理的方法，求一次差分后序列的平稳性大大增强。本文通过LS+AR模型预报精度达到国际领先水平。国内外对EOP的预报绝大多数没有考虑基础序列长度对EOP预报精度的影响，本文通过试验发现基础序列长度越长，其预报精度反而越差，以6年作为基础序列长度比较合适。

1 党亚民，秘金钟，成英燕.全球导航卫星系统原理与应用［M］.北京:测绘出版社，2007.(Dang Yamin，Mi Jinzhong and Cheng Yingyan.Principles and applications of global navigation satellite system［M］.Beijing:Chinese Surveying and Mapping Press，2007)

2 王琪洁.基于神经网络技术的地球自转变化预报［D］.中国科学院上海天文台，2007.(Wang Qijie.The earth rotation changes prediction based on neural network technology［D］.Shanghai Astronomical Observatory，2007)

3 Yang Y X and Cui X Q.Adaptively robust filter with multi adaptive factors［J］.Survey Review，2008，40(309):260 -270.

4 许雪晴，周永宏.地球定向参数高精度预报方法研究［J］.飞行控制学报，2010，29(2):70-76(Xu Xueqing and Zhou Yonghong.The research of the earth orientation parameters high accuracy prediction method［J］.Journal of Flight Control，2010，29(2):70-76)

5 钱昌夏.极移速度的周期分析［J］.中国科学院上海天文台年刊，1995，16:35-40.(Qian Changxia.Periodic analysis of velocity of polar motion［J］.Annals of Shanghai Observatory Academia Sinica，1995，16:35-40)

6 韩永刚，李志安.地球自转速率变化主要中短周期的分析［J］.地球物理学进展，2002，17(2):349-352.(Han Yonggang and Li Zhian.Analysis of main middle and short periods in the variation of the Earth’s rotation［J］.Progress in geophysics，2002，17(2):349-352)

7 张善文，雷英杰，冯有前.MATLAB在时间序列分析中的应用［M］.西安:西安电子科技大学出版社，2007.(Zhang Shanwen，Lei Yingjie and Feng Youqian.Application of MATLAB in time series analysis［M］.Xi’an:Xi’an University of Electronic Science and Technology Press，2007)

8 王新洲，等.高等测量平差［M］.北京:测绘出版社，2006.(Wang Xinzhou，et al.Advanced surveying adjustment［M］.Beijing:Chinese Surveying and Mapping Press，2006)

9 李征航，等.空间大地测量学［M］.武汉:武汉大学出版社，2010.(Li Zhenghang，et al.Space geodesy［M］.Wuhan:Wuhan University Press，2010)

SHORT-TERM PREDICTION METHODS AND REALIZATION OF EARTH ROTATION PARAMETERS

Yan Feng and Yao Yibin
(School of Geodesy and Geomatics，Wuhan University，Wuhan 430079)

According to the respective characteristics of polar motion and length of day，combining LS and AR model，a suitable prediction model for the Earth Rotation Parameter(ERP)was builded.In order to reduce the strong correlation，the difference before establishing AR model was down and ERP 1-10 days were predicted.The results show that the prediction accuracy has reached an international leading level.

the Earth rotation parameters(ERP);trigonometric polynomial model;auto-regressive model;prediction accuracy;stationary test

1671-5942(2012)04-0071-05

2012-01-24

国家自然科学基金创新研究群体项目(41021061);国家自然科学基金(41174012)

严凤，女，硕士生，主要研究方向为地球自转参数短期预报.E-mail:642304401@qq.com

P227;P207

A