最小二乘法在汽车销售量预测中的应用

□文/陈秋玲 陈 忠

（武汉理工大学理学院 湖北·武汉）

对产品销量进行预测是进行经济决策活动的一个重要组成部分。运用定量预测模型对产品销量进行预测方法有很多，本文运用的最小二乘法在产品销售量预测过程中，使用的方法简单明了，比较适合企业在进行预测产品产量时作为参考，从而能够避免盲目的生产和经营，尽可能地为企业获得最大利润，以减少不必要的损失。

一、最小二乘法

在介绍最小二乘法之前，我们先来思考这个问题。如果变量y和x有精确的线性关系，这里可以假设y为因变量，x为自变量，有y=a1x+a0成立，我们得到，即观测值等于回归值。但是，在现实世界中，变量之间的关系未必都是线性的。受各种随机因素的干扰，物与物之间没有非常明确的对应关系。比如，产品的销售量和供给量就是一种对应关系，而这种关系并非是y=a1x+a0所能确定的。那么，我们要得到销售量和供给量之间的关系，就需要通过数学方法来建立销售量和供给量之间的模型。而在处理类似的问题时，我们常常用到的是最小二乘法。

所谓最小二乘法，就是选择合适的参数a0、a1，使得全部观测的残差平方和最小。用数学公式表示为:

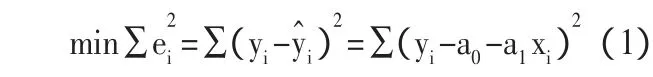
为了说明这个方法，先解释一下最小二乘原理。因为不能利用总体回归方程进行参数估计，所以我们选择样本回归函数对总体进行估计，即:

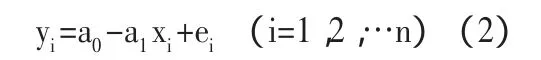
（2）式中:ei是残差，等于真实值 yi减去估计值i。因此，为了使残差ei尽可能的小，就需要选择合适的估计量a0，a1，使总体回归函数最优。

在经济关系中，某一指标Y往往与多个因素X1，X2，…，Xm有关，如果这种关系具备一定的线性相关性，我们就可以利用多元回归分析来处理这组数据。假设，我们令Y、X向量分别为:Y=（y1，y2，…，yn），X1=（x11，x21，…，xn1），X2=（x12，x22，…，xn2），Xm=（x1m，x2m，…，xnm），由X1，X2，…，Xm与Y之间存在的线性关系，得到n元线性预测公式:

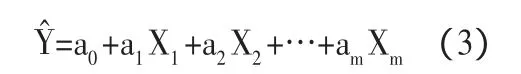
其矩阵形式为:

其中，我们称待定常数 a0，a1，…，am为回归系数。将每组观测值代入（4）就得到:

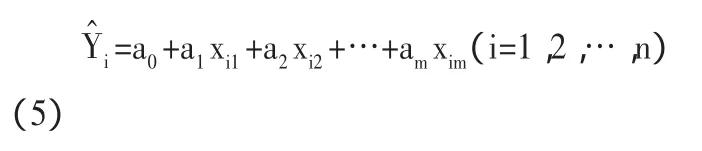
选择的a0，a1，…，am，应使每个偏差e（ii=1，2，…n）都尽量小，因此，我们通常令偏差平方和为最小。这里，我们把S视为a0，a1，…，am多元函数，即:

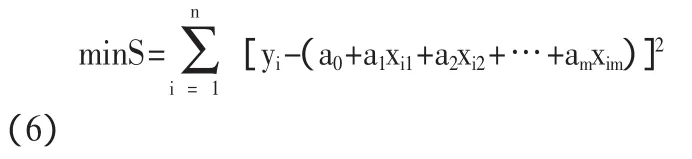
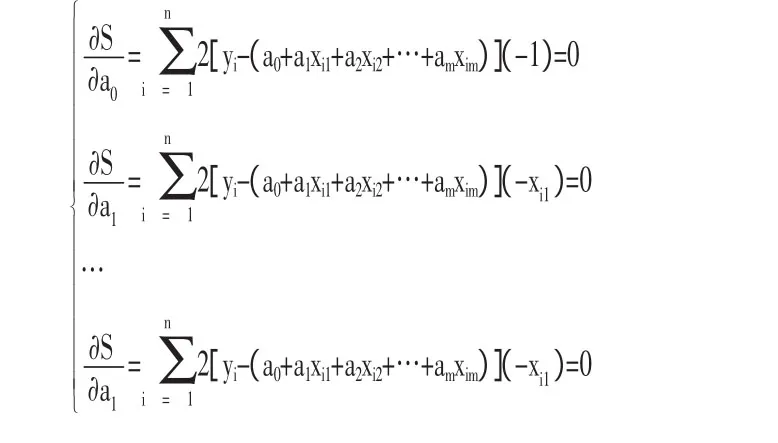
整理得:

将上述m+1个方程式联立起来求a0，a1，…，am解，则得到公式（6）的待定系数值，从而确定了多元线性预测公式。

二、相关系数R

以两个变量的情况为例，只要任意给定两个变量x，y的一组数据，都可以经过计算给出一个经验公式，但是这个公式在多大程度上反映了x，y的关系呢？因为只要通过最小二乘法采取强拟合我们同样可以把一组毫无线性关系的数据表成线性关系，但这条直线并不能很好地反映了变量x和y的实际关系，缺乏应用价值。

为此，我们一方面要建立从经验上认为有意义的方程，另一方面我们必须用数学方法对拟合效果和显著性进行相关检验。相关系数是变量之间相关程度的指标，求相关系数的公式为:

表1 2001～2011年某纺织品销售额数据表

由上面的式子可推算出:

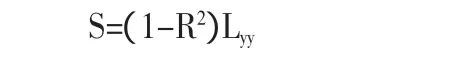
由于 S≥0，Lyy=≥0，我们可以得出 1－R2≥0，即 0≤≤1，所以越接近1，S的值就越接近0，x，y的线性关系就越好。

三、实例预测

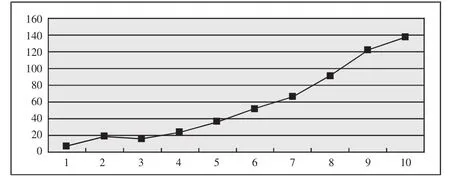
图1 某品牌汽车2002～2011年总销量曲线图

表2 经验公式拟合处理后数据表

例:对某汽车品牌的汽车销售量的拟合。我们选取汽车销售量为因变量，单位为千辆，拟合销售量关于时间x的趋势曲线。以2002年为基准年，取值x=1；2011年x=10，2002～2011年的数据如表1。（表1）由散布图1可以看出统计点是非线性的，它大致呈指数形分布。我们就取经验公式y=αeβx来拟合这条曲线。（图1）这个经验公式所反映的点的排列是非线性的，我们可以通过取对数将其转化为线性函数，从而运用最小二乘法确定这个线性函数。即:z=Ax+B，其中 z=lny，A=β，B=lnα，lny=lnα+βx，进而计算 α，β 的值。

取；xi=（1，2，…，11）；yi为各年销售额；zi=lnyi，根据具体数据代入得到表格2。（表2）

查对数表得 α=6.746，将 β，α 代入（8）式中，因此得到了所求的经验公式为:

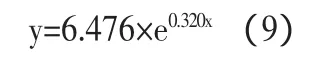
下面计算相应系数进行显著性检查:

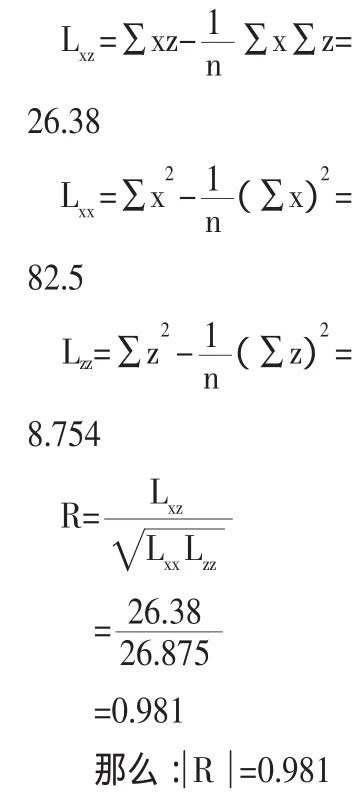
查看关系表（按α=0.01，n－2=11－2=9）得到回归临界值γα=0.735， 因 为=0.751＞γα=0.735，说明x，y间存在强相关关系，可以按公式:y=6.746×e0.320x进行外推预测，预测该企业2012年和2013年的销售额为:

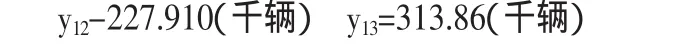
以上是根据散点分布趋势选取曲线来拟合得出的结果，那么如果我们强行用线性关系即:=Ax+B来拟合曲线，会得出怎样的结果呢？运用强行用线性关系，我们有:

四、小结

通过对具体实例的分析我们发现，如果某种产品在一个时期内销量处于稳定增长的状态，我们就可以对此种产品的未来销量运用最小二乘法进行预测。但是，在选用曲线来拟合散点的过程中，我们必须依据散点的发展趋势来正确的选择曲线，否则有可能出现类似本文实例中出现的情况，即两条曲线的显著性系数都符合要求，都可以用来进行预测，但由于其中的一条拟合曲线没有分析散点的发展趋势，最后导致产生的误差太大，因而不适宜运用在产品销量的预测上。所以，企业在日常生产管理销售过程中，科学有效的预测方法将在很大程度上决定企业的利润，从而给经营者制定或者调整销售计划提供了可靠的理论依据。

[1]韩於羹.应用数理统计[M].北京:北京航空航天出版社，1989.

[2]徐天群，董亚娟.应用数理统计学习指导[M].武汉:武汉大学出版社，2002.

[3]方开泰，全辉等.实用回归分析[M].北京:科学出版社，1988.

[4]岳苓水，赵宝贵.最小二乘法在商品销售预测中的应用[J].石家庄:地质技术经济管理，1997.1.

[5]杜国毅.最小二乘法在经济预测中的应用[J].呼和浩特:内蒙古统计，2001.6.

[6]张金力，陈广伏.最小二乘法在计量经济模型中的应用[J].沈阳:沈阳航空工业学院学报，1999.4.