基于BIOCHLOR模型的敏感度分析

陆晓暖，陈世俭

(中国科学院测量与地球物理研究所，武汉 430077)

1 研究背景

自1952年，Lapidus和Amundson提出类似对流－弥散方程(CDE)的模拟模型，溶解质运移研究已有近60年的历史。随着研究的深入，国内外研究者不断取得了显著成果。如Nielson建立了溶质运移理论研究的经典方程——CDE方程，并首次系统论述了其合理性和科学性［1］。目前，国内外对地下水溶质运移模型的研究已有相当的水平，相应的数学模型也日趋成熟，加上计算机的普及及其性能的急剧提高，地下水溶质运移模拟软件也相继问世，并且日趋成熟［2］。美国地质调查局McDonald博士等设计出三维有限差分模拟程序MODFLOW，加拿大WHI公司的Visual Modflow，以及美国地下水服务中心设计的BIOCHLOR等都是目前较为流行的地下水水质模拟软件。

随着模拟软件的广泛应用，模型本身对参数的敏感度也逐渐被使用者所关注，向研究者提出了模型敏感度分析的要求。敏感度分析，即一种确定模型各个参数对模型模拟结果影响程度的一种手段。在运用模型模拟过程中，模型的敏感度分析是处理参数的测量误差或区域间参数选择的重要依据，具有较高的研究意义。

2 模型介绍

BIOCHLOR是一种以微软EXCEL电子表格模块为支持平台，基于DOMENICO溶质运移分析模型开发而来的，用于模拟在氯化物溶质排放点自然降解修复过程中氯化物溶质运移的简易界面模型。由于应用微软 EXCEL电子表格为支持平台，BIOCHLOR具有以下优点:①减少研发成本;②可综合利用EXCEL的强大功能;③模块简明，运行简便，输出明确，模拟效果较好等，被广泛用于一维平流、三维弥散、线性吸附及还原脱氯的生物降解过程分析。BIOCHLOR模型共有7个参数模块:平流参数、扩散参数、吸附参数、生物降解参数(一阶序列降解系数)、常规数据、污染源数据及野外实测数据。模型包括3种模拟类型:①不考虑降解的溶质运移;②一阶序列降解下溶质运移;③2个不同反应区一阶序列降解下溶质运移。

BIOCHLOR最初为模拟聚氯乙烯和乙烯的序列降解设计，用于模拟伴随一阶序列降解下聚氯乙烯或乙烯及其降解中间产物及最终产物的运移过程。以六氯乙烯(PCE)为例，其一阶生物降解过程如图1所示:六氯乙烯(PCE)在序列降解过程中依次生成三氯乙烯(TCE)、二氯乙烯(DCE)、一氯乙烯(VC)，最后完全脱氯为无毒的乙烷(ETH)［3］。

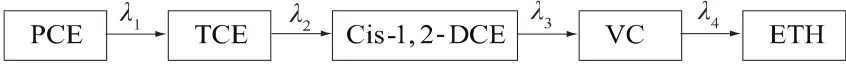
图1 六氯乙烯(PCE)一阶生物降解过程Fig.1 The sequential decay of Chlorinated Ethenes

BIOCHLOR利用分析模型DOMENICO模型计算在一阶序列降解以及污染源衰退的情况下(如图2所示)，污染羽内各溶解质 PCE，TCE，DCE，VC，ETH 的浓度分布及其变化。其方程式可以表达为

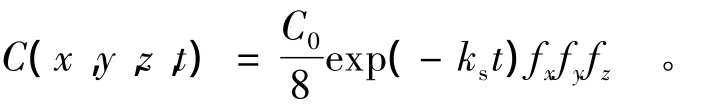
其中:

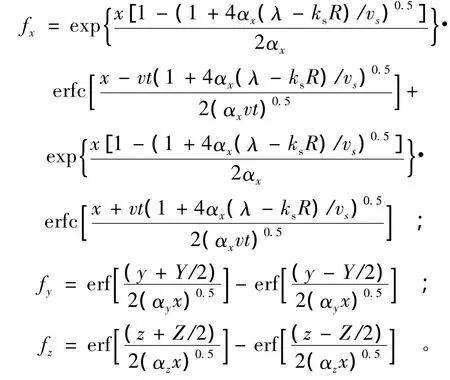
式中:erfc，erf分别为互补误差函数和误差函数;C(x，y，z，t)为在t时污点(x，y，z)的某溶质浓度;C0为t=0时污染源的溶质浓度(mg/L);x为距污染源底端距离(m);y为距污染羽纵向中心线距离(m);z为距饱和带顶端距离(m);αx地下水纵向扩散能力(m)，αy地下水侧向扩散能力(m);αz地下水垂直扩散能力(m);ne为土壤孔隙度;λ为一阶序列降解系数(a－1);Vs为下渗速度(m/a);v为化学流速(m/a);R为延迟系数;i为水力梯度力;Y为污染源宽度(m);Z为污染源厚度(m)，Ks为污染源降解常数(1/a)［4－5］。

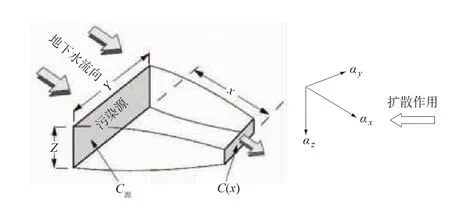
图2 DOMENICO模型示意图Fig.2 Sketch of the DOMENICO model

3 研究方法

本文主要研究方法即选择用于检验模型敏感度的参数以及用于表征模型响应程度的输出结果，通过改变参数，运行模型，记录模拟结果，利用EXCEL，SPSS对模拟结果和参数进行数据处理和分析，通过回归分析，获得模拟值与各参数的函数关系，并对各函数求导，进行进一步分析比较。

3.1 分析参数的选择

BIOCHLOR模型共有平流参数、扩散参数、吸附参数、生物降解参数(一阶序列降解系数)、常规数据、污染源数据及野外实测数据7个参数模块，其中常规数据与污染源数据是对模型模拟的初始设置。常规数据是对模拟的时空设置，包括模拟时间、模拟区域的长与宽的设定。污染源数据则是对污染源的描述，包括厚度、宽度及污染源内污染物空间分布的初始情况等。另外，野外实测数据用于模型验证，与常规数据、污染源数据对 BIOCHLOR模型起初始设置或辅助模拟验证作用，不作为此次敏感度分析的参数。

在此次敏感度分析中，选择了平流参数模块、扩散参数模块、吸附参数模块、生物降解参数模块(一阶序列降解系数)等参数，这些参数BIOCHLOR模型本身自带有特定赋值，直接针对已有参数值进行调整即可。本文4个参数作为调整参数，将这4个参数模块对应的参数Vs，αx，R，λ分别设定为初始值(Vs=34，αx=12.2，R=2.9，λ1=2，λ2=1，λ3=0.7，λ4=0.4)的0.1，0.5，1，1.5，2倍，在其他6个参数不改变的情况下，对每个参数依次调整，记录输出结果，进行分析。其中扩散参数中的延迟因子R取值不能小于1，根据模型本身默认值2.9，则不能取到其0.1倍，在本文中用最小值1替换。

用于分析的4个参数:平流参数、扩散参数、吸附参数及生物降解参数，是影响地下水中溶质运移的4个基本因素。在BIOCHLOR模型中，平流参数模块主要是求得渗透速率Vs。扩散参数模块主要提供研究区纵向、侧向、垂向上的弥散度，即αx，αy，αz，给定αx后模块可根据已输入的比例系数自动计算出αy，αz。吸附参数模块则是对延迟因子R的计算。生物降解参数模块即求解污染源上、下游不同要素的一阶序列降解系数(λ)。

3.2 模型响应指标的选择

模型的输出项中包括六氯乙烯(PCE)、三氯乙烯(TCE)、二氯乙烯(DCE)、一氯乙烯(VC)以及无毒的乙烷(ETH)5 种溶质在距污染源0，33.1，66.1，99.4，132.3，165.5，198.4，231.6，264.6，297.8，330.7 m处的浓度。其中以165.5 m出的TCE浓度在初始模拟中模拟值与实测值最为接近，且敏感度分析中表现出较灵敏的响应，故在本文选择165.5 m出的TCE浓度作为敏感度分析的响应指标，用于表征模型对分析参数的响应情况。

4 结果与分析

模型敏感度分析，就是通过改变模型的输入参数来检验模拟结果的总体响应，检验模型输入参数的不确定性是否引起模拟结果的不确定性，并且可指导野外调查工作的一种针对模型的分析手段。本文中介绍BIOCHLOR模型敏感度分析，主要是针对一阶序列降解下溶质运移这一模型类型，通过调整7个输入参数模块中的平流参数、扩散参数、吸附参数及生物降解参数4个参数，来检验该模型的模拟结果对各个参数的响应程度。

对通过改变平流参数、扩散参数、吸附参数及生物降解参数4个参数获得的165.5mt处的TCE浓度，通过绘制散点图，选择最优的回归模型，对模拟值与各参数进行相关分析和回归分析，获得相应回归结果，并绘制曲线图。其中获得的回归函数可表示为:

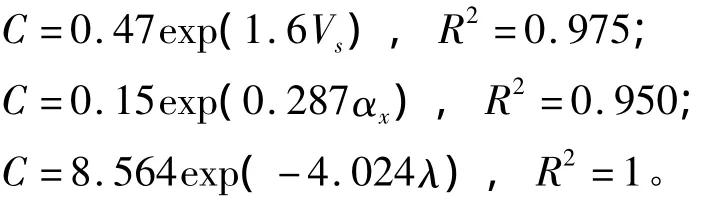
其中:C 表示165.5 m处TCE 浓度(mg/L);Vs，αx，λ分别表示下渗速度、扩散能力、一阶序列降解速率;R2为方程的确定性系数。3个回归函数及其导函数的曲线图如下图所示。

图3展现的是距污染源165.5 m处TCE的浓度与下渗速度的关系，二者呈现出指数函数关系。图4中的导数函数则展示TCE浓度随下渗速度变化而变化的程度。如图所示，TCE浓度随下渗速度的增加而指数增加，且增加速率随下渗速度增加而增大。由此可见，模型的模拟预测值对平流参数具有相当的敏感度，且敏感度随下渗速度增加而呈指数增大。

图3 165.5 m处TCE浓度与下渗速率的函数曲线Fig.3 Function curve of TCE concentration at 165.5m away from the pollution source vs.seepage velocity

图4 165.5 m处TCE浓度与下渗速率函数的导数曲线Fig.4 Derivative curve of TCE concentration at 165.5m away from the pollution source vs.seepage velocity

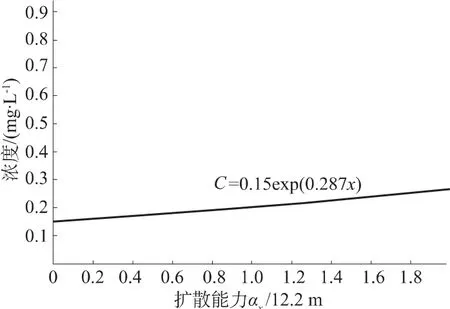
图5 165.5 m处TCE浓度与扩散能力的函数曲线Fig.5 Function curve of TCE concentration at 165.5m away from the pollution source vs.dispersivity

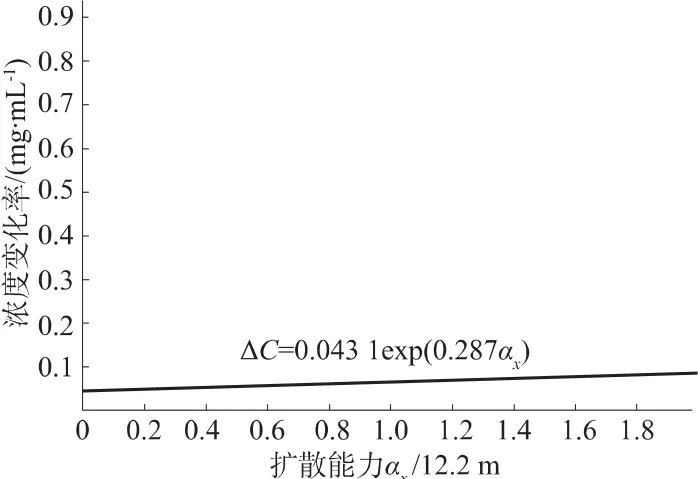
图6 165.5 m处TCE浓度与扩散能力函数的导数曲线Fig.6 Derivative curve of TCE concentration at 165.5m away from the pollution source vs.dispersivity

由图5可见，距污染源165.5 m处的TCE浓度随扩散能力，增大而缓慢增加。同时，从图6可看出，TCE浓度随扩散速度增大而变化的速率也相对平稳，呈极小的坡度上升。总而言之，BIOCHLOR模型对扩散参数存在很弱的敏感度，且扩散速度越小，模型敏感度越弱。

图7中的曲线体现出165.5 m处TCE浓度随一阶序列降解速率增加而呈指数迅速递减的关系，且图8中的导函数曲线说明一阶序列降解速率越小该递减速率越大，随着一阶序列降解速率增加，TCE浓度递减速率由急剧下降逐渐转向缓慢下降，尤其在一阶序列降解速率大于2a－1时，递减速率相对平缓且趋于零。

此外，在模型模拟过程中，165.5 m处TCE浓度对吸附因子R表现出极弱的敏感度，当R取最低值及初始值的0.5，1，1.5倍，即R=1，1.45，2.9，4.35时，TCE浓度都无丝毫变化，仅在R取初始值的2倍，即R=5.8时，TCE 浓度才表现出0.003 mg/L 的减少。模拟表明模型对吸附参数极不敏感。

比较而言，模型对吸附参数最不敏感，响应极其微弱。其次是扩散参数，模型对此参数响应相对不明显。平流参数和生物降解参数对模型影响较大，尤其是当下渗速度较大或者一阶序列降解速率较小时，模型表现出相当灵敏的响应。

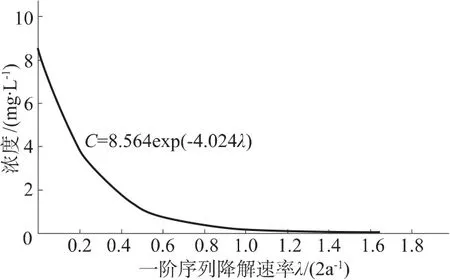
图7 165.5 m处TCE浓度与一阶序列降解速率的函数曲线Fig.7 Function curve of TCE concentration at 165.5m away from the pollution source vs.first-order degradation rate coefficient

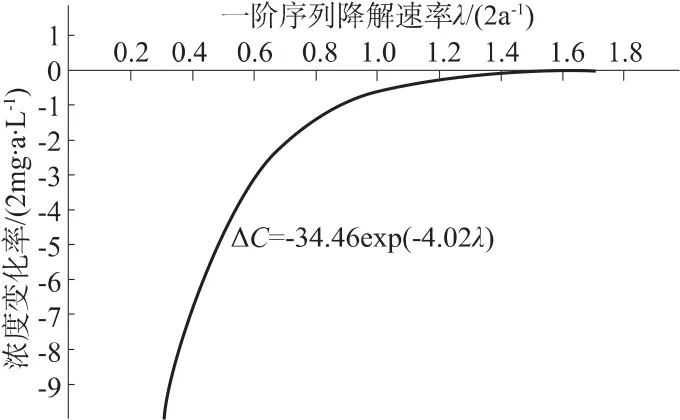
图8 165.5 m处TCE浓度与一阶序列降解速率函数的导数曲线Fig.8 Derivative curve of TCE concentration at 165.5m away from the pollution source vs.first-order degradation rate coefficient

5 结论

(1)除对吸附参数外，模型对分析参数还表现出不同程度的敏感度。这就对输入参数提出了较高的精度要求，尤其对平流参数和生物降解参数，在参数的获取、计算过程中应相应投入较大的工作量，以确保模型模拟的精确性。

(2)各个分析参数对模型的影响均体现出一定规律和特性。吸附因子不论取值大小，对模型的影响均微乎其微。模型对扩散参数的敏感度较吸附参数大，但依旧微弱。模型对平流参数体现出较大的敏感度，且随下渗速度增加，敏感度指数增高。生物降解参数则正相反，一阶序列降解速率越小，模型对其响应越灵敏。

(3)本次模拟分析中，以距污染源165.5 m处TCE浓度作为模型输出结果的表征，虽具有较高的准确性和代表性，但本模型的输出项众多，单一的表征指标未必能对每项输出结果都能准确代表，在进一步的研究中应做更全面、细致的工作。

(4)本次研究仅仅是经过简单调参来检验模型敏感度，缺乏实际研究区数据进行检验，存在一定主观性，需要进一步改进和深入研究分析。

［1］高川博，姜 斌，黄国强，等.土壤污染物溶质运移模型研究进展［J］.环境保护科学，2006，32(5):44－46.(GAO Chuan-bo，JIANG Bin，HUANG Guo-qiang，et al.Research Development of Polluted Solute Transport Model in Soil［J］.Environmental Protection Science，2006，32(5):44－46.(in Chinese))

［2］薛红琴.地下水溶质运移模型应用研究现状与发展［J］.勘察科学技术，2008，(6):17－22.(XUE Hongqin.Present Situation of Application Research on the Mathematic Model of Groundwater Solute Migration and Its Development［J］.Site Investigation Science and Technology，2008，(6):17－22.(in Chinese))

［3］VOGEL T M，MCCARTY PL.Abiotic and Biotic Transformations of 1，1，1-Trichloroethane under Methanogenic Conditions［J］.Environmental Science and Technology，1987，21(12):1208－1213.

［4］DOMENICO P A.An Analytical Model for Multidimensional Transport of Decaying Contaminant Species［J］.Journal of Hydrology，1987，91(1/2):49－58.

［5］MARTIN-HAYDEN J M，ROBBINS G A.Plume Distortion and Apparent Attenuation Due to Concentration Averaging in Monitoring Wells［J］.Ground Water，1997，35(2):339－346.

［6］于顺东，尤学一.WASP水质模型检验及参数敏感度分析［J］.水资源与水工程学报，2007，18(6):41－44.(YU Shun-dong，YOU Xue-yi.Testing WASP Water Quality Model and Sensitive Analysis for the Parameters［J］.Journal of Water Resources and Water Engineering，2007，18(6):41－44.(in Chinese))

［7］杜恩昊，张佳宝，唐立松.一种溶质运移数学模型的应用研究［J］.干旱区研究，2001，18(1):29－34.(DU En-hao，ZHANG Jia-bao，TANG Li-song.Application of a Solute Transport Model in Field Scale［J］.Arid Zone Research，2001，18(1):29－34.(in Chinese))