关系代数中除法运算相交算法的探讨*

卫 娟，戴 冬

（河南机电高等专科学校计算机科学与技术系，河南 新乡 453000）

1 引言

关系运算理论是施加于关系上的一组高级运算，是关系数据库查询语言的理论基础。关系数据库之所以取得了巨大成功和广泛应用，就是因为它具有适合关系运算的集合运算、投影、连接、选择和除法运算的数学基础，以及以这些运算为基础而建立起来的其他各种运算;从而可以对二维表格形式的关系进行任意的分割和组装，构造出用户所需的各种表格，方便实现对数据库的查询、插入、修改和删除。

在关系代数运算中，交、除法、连接、自然连接四种运算可以用集合理论定义外，还可以用并、差、广义笛卡尔积、投影和连接五种基本关系代数运算表示。其中，除法运算相对于选择、投影、连接来说是较难的一种运算。

除的引入其实是一个反问题的问题，如关系表学生选课表(学号、课程号、成绩)、学生表(学号、姓名、性别、年龄、籍贯)、如何查找出被全部学生都选修的课程号，则要用到除法。

除法是写为R÷S的二元关系。其结果由 R中元组到唯一于R的属性名字(就是说只在R表头中而不在S表头中的属性)的限制构成，并且它们与S中的元组的所有组合都存在于 R中［1］。

在关系运算中，除法运算可理解为笛卡尔积的逆运算。设被除关系R为r元关系，除关系S为s元关系，那么它们的商为r-s元关系，记为R÷S。商的构成原则是:将被除关系R中的r-s列，按其值分成若干组，检查每一组的s列值的集合是否包含除关系S，若包含则取r-s列的值作为商的一个元组，否则不取［3］。

2 除法定义的理解

除运算是同时从关系的水平方向和垂直方向进行运算。设两个关系R和S的元数分别为r和s(r＞s＞0)，那么R÷S是一个(r-s)元的元组的集合。(R÷S)是满足下列条件的最大关系，其中每个元组t与S中每个元组u组成的新元组必在关系R中［2］。

R÷S的具体计算过程如下:

假设关系S的属性是关系R中后面的s个属性，则R÷S的算法如下所示:

第一步:计算 R 的投影:T=π1，2，…，r-s(R)

第二步:计算T×S中不在R中的元组:V=(T×S)-R

第三步:计算 V 的投影:W=π1，2，…，r-s(V)

第四步:计算结果:R÷S=T-W

3 算法实例讲解

例题1:已知关系R和S如图1所示。其中，R中有属性 A、B、C、D，S中有属性 C、D，求 R ÷S的运算结果。

R

图1 表R和表S

根据算法可知，r=4，s=2，所以有:

(1)计算 T=π1，2(R)，结果如图2所示。

图2 π1，2(R)结果集

(2)计算T×S中不在R中的元组:V=(T×S)-R，结果如图3所示。

图3 (T×S)-R结果集

(3)计算V的投影:W=πA，B(V)，结果如图4所示。

图4 πA，B(V)的结果集

(4)计算R÷S，结果集(1)如图5所示。

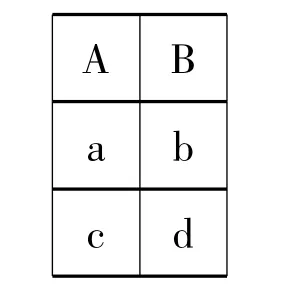
图5 R÷S结果集(1)

通过上述例题的计算过程，可以了解到，虽然此种方法步骤比较清晰，但此算法比较麻烦，求解步骤较多，每一步都必须谨慎，过程较为繁琐，而且理解起来也比较难，算法较为费时。如果在计算过程中稍有不慎，则会造成整个计算结果错误的后果。

4 新算法的提出

经过对常用算法的介绍和举例说明，已经较为清楚除法的计算过程。下面提出一种相交算法。此方法相对较为简单且容易理解，学习起来较为容易。

设关系R和S的目数分别为r和s，且r＞s，S≠Ø。求R÷S。

算法分以下几个步骤:

(1)∏1，2，…，s(S);

(2)按∏1，2，…，s(S)的元组求其在 R 中的映像。

(3)求映像的交集。

用上例中的例题，具体求解步骤为:

(1)S 中(C，D)的取值为{(c，d)，(e，f)}。

(2)假设{(c，d)，(e，f)}在 R 中的投影分别是M和N:

M={(a，b)，(e，d)}

N={(a，b)，(b，c)，(e，d)}

(3)求M和N的交集。

M∩N={(a，b)，(e，d)}

所以R÷S的结果集(2)如图6所示。

图6 R÷S结果集(2)

通过上述的算法介绍，可以看只要将每一个除数中的元组在被除数中的象集找到，然后再求象集的交集，则会很快地求出除法的结果。由此可以看出此算法容易掌握，而且计算速度也较快，使人容易接受此种算法。

5 结语

除法运算较为难理解和掌握，所以在做除法运算时，不能急于求成，要根据算法和步骤进行计算。除法的运算方法还有其他的算法，例如求象集等方法，但不论是哪种算法，都要对算法熟悉，并要熟练的掌握。要对除法有熟练的掌握，可以通过做大量的习题来达到目的。本文提出的相交算法相对于其他算法来说，学习起来比较容易理解和掌握，在一定意义上说解决了除法运算在理解难及掌握难方面的问题。

［1］李俊山.数据库原理及应用(SQL Server)［M］.北京:清华大学出版社，2009.

［2］狄文辉.数据库原理及应用——SQL Server［M］.北京:清华大学出版社，2008.

［3］石玉强.数据库原理及应用［M］.北京:中国水利水电出版社，2009.