周期脉冲序列作用下单模激光线性模型的随机共振

汪志云, 陈培杰, 张良英 (湖北文理学院物理与电子信息工程学院，湖北 襄阳 441053)

周期脉冲序列作用下单模激光线性模型的随机共振

汪志云, 陈培杰, 张良英 (湖北文理学院物理与电子信息工程学院，湖北 襄阳 441053)

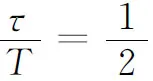
激光光学；周期脉冲序列；功率谱；信噪比；随机共振

在现代激光通信中，激光常被用来作为信号的传送器，由于激光系统中存在量子噪声和抽运噪声，激光器的工作总是伴随着涨落的出现。如何减小激光输出光强的涨落，消除和抑制噪声对传输信号的影响，增加激光的输出稳定性，一直是提高激光器和激光通信质量的重要研究课题并取得了较大进展，为优化激光通信系统提供了理论依据[1-2]。

对于单模激光系统，曹力等[3-5]首次将信号与考虑关联的泵噪声和量子噪声相乘的形式引入单模激光系统，运用线性近似的方法，在激光系统中发现了信噪比随关联强度的变化出现单峰的随机共振。张良英等[6-14]运用该方法，研究了不同噪声驱动下的单模激光增益线性模型初态和瞬态的随机共振现象，以及调幅波和调频波在各种关联噪声驱动下单模激光系统的随机共振。在上述研究工作中，输入的信号都采用周期余弦信号，而对于周期脉冲序列作用下的单模激光系统随机共振的研究很少。为此，笔者构建周期脉冲序列信号和白噪声共同驱动下单模线性激光模型，通过傅里叶级数展开的方法处理脉冲信号，计算了输出信号的功率谱和信噪比，讨论了系统中的随机共振现象。

1 周期脉冲序列和白噪声驱动下的单模激光信噪比

单模激光线性增益模型在输入周期矩形脉冲序列后的光强方程为:

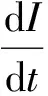
(1)

式中，I为激光光强；β和Γ分别为自饱和系数和增益系数；K为损失系数；ξ(t)和η(t)分别为泵噪声和量子噪声；D为量子噪声强度；f(t)为周期矩形脉冲序列，在1个周期内其表达式为：

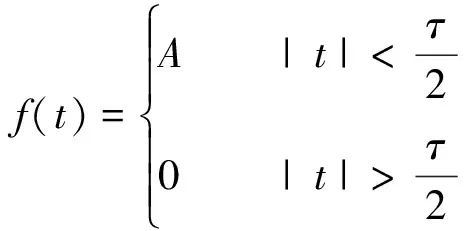
(2)

泵噪声和量子噪声的统计性质为：

〈ξ(t)〉=〈η(t)〉=0 〈ξ(t)ξ(t′)〉=Qδ(t-t′) 〈η(t)η(t′)〉=Dδ(t-t′)

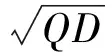
(3)

式中，λ为噪声关联系数；Q为泵噪声的强度。

将信号f(t)展开为三角形式傅里叶级数：

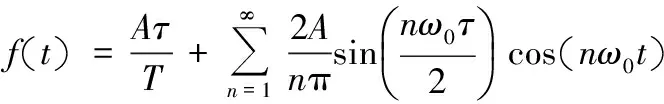
(4)

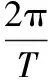
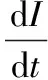
(5)

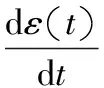
(6)

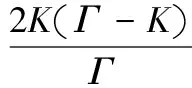
由式(6)可解得：

(7)

根据平均光强相关函数的定义：

由式(3)和式(7)可以求得〈ε(t)〉、〈ε(t+t′)〉和〈ε(t)ε(t+t′)〉，代入式(8)可以得到平均光强相关函数(γ≠τ-1)：

(9)

将式(9) 式进行坐标平移，去掉常数项后进行傅里叶变换，得到光强功率谱为：

S(ω)=S1(ω)+S2(ω)

(10)

式中，S1(ω)为输出信号功率谱；S2(ω)为输出噪声功率谱：

S1(ω)中包含2个δ函数，若只取正ω的谱，其表达为：

(11)

S2(ω)在各个频率处的表达式为：

(12)

由式(11)可得到输出信号的总功率为：

(13)

将输出信号总功率与输出信号中各个频率处单位噪声功率之和的比值定义为信噪比(SNR)，即：

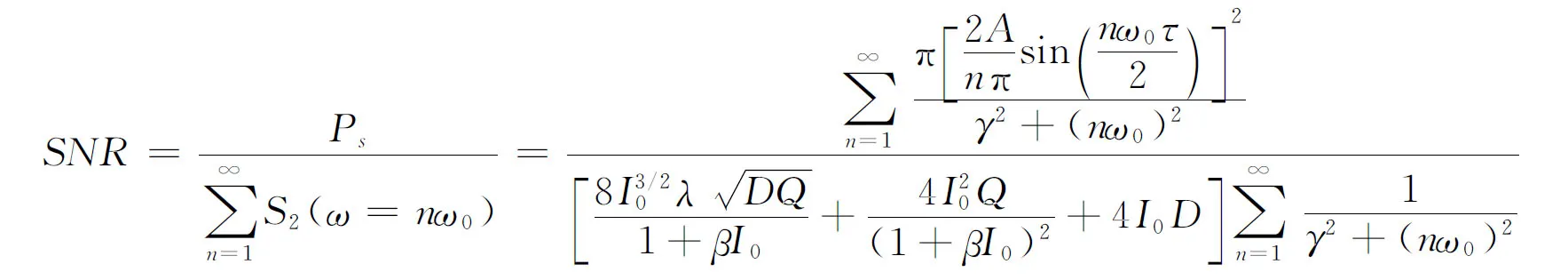
(14)

2 输出信号光强的随机共振

2.1信噪比随泵噪声强度Q和量子噪声强度D的变化

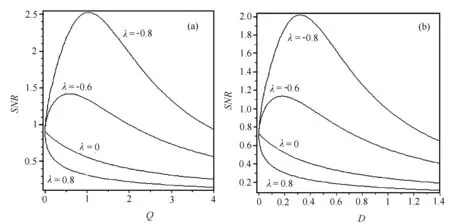
图1 信噪比SNR在不同的噪声关联系数λ下随噪声强度Q和D的变化

根据式(14)在噪声关联系数λ取不同值时，信噪比(SNR)随泵噪声强度Q和量子噪声强度D的变化曲线如图1所示。从图1可以看出，不同λ值的SNR-Q和SNR-D曲线的起点相同；当λ≥0时，信噪比随噪声强度单调减小，没有出现随机共振现象；在λlt;0时，信噪比随噪声强度的变化均出现了随机共振现象，峰值随|λ|的增大而增大，其位置向右移动。上述现象是传统的随机共振现象，与周期余弦信号作用下的单模激光随机共振现象是相同的。

2.2周期脉冲信号对光强随机共振的影响

图2所示的是脉冲振幅、周期和脉宽不同时信噪比SNR随泵噪声强度Q的变化曲线。当输入信号振幅增大时，SNR-Q曲线整体上移，其共振峰变得更加尖锐，峰值的位置并不发生改变(见图2(a))。当脉冲宽度τ=0.6、脉冲周期T取不同值时，SNR-Q共振曲线的起点不相同，峰值的位置不发生改变；当脉冲周期Tlt;1.2(2τ)时，随着T的增大，SNR-Q曲线的共振峰增高，且更加尖锐；而当Tgt;1.2(2τ)时，共振峰却随着T的增大而降低(见图2(b))。当脉冲周期取定值(T=1)，脉宽τ取不同值时，SNR-Q曲线的峰值大小不同，其位置相同；在τlt;0.5(T/2)时，曲线的共振峰随τ的增大而升高；当τgt;0.5(T/2)时，SNR-Q曲线的共振峰随τ的增大而降低(见图2(c))。上述现象说明脉冲宽度和周期对SNR-Q共振曲线的影响基本相同。

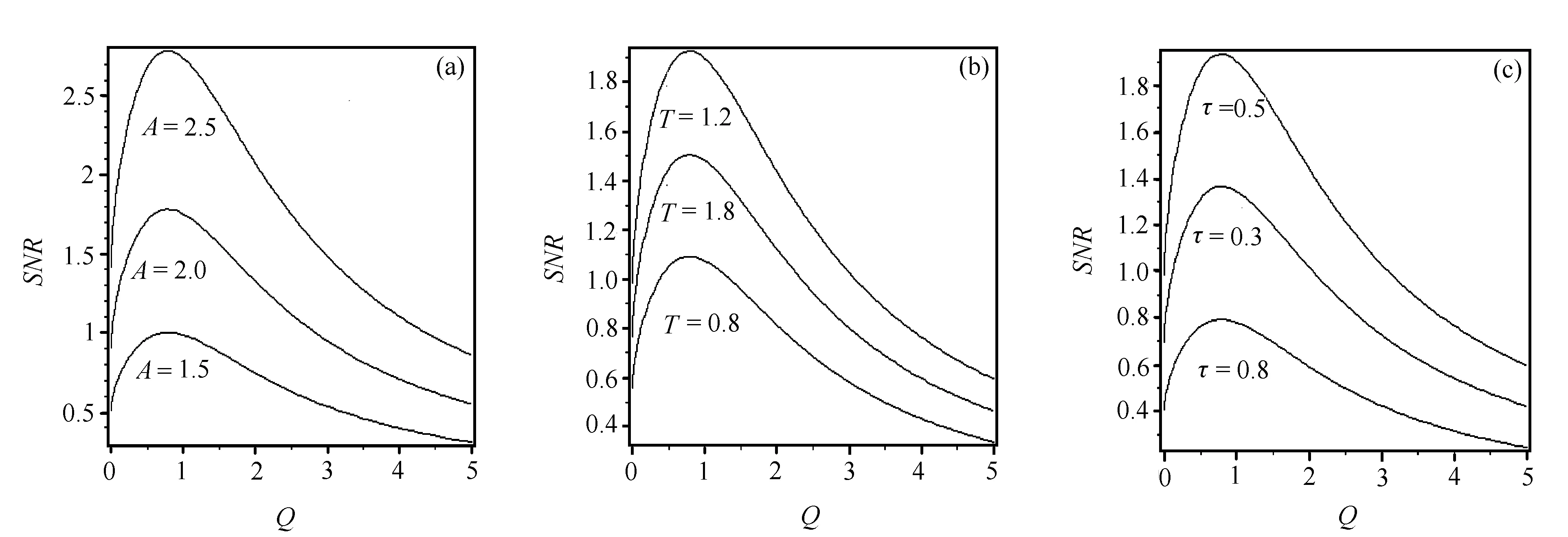
图2 脉冲振幅、周期和脉宽不同时信噪比SNR 随泵噪声强度Q的变化

2.3信噪比随脉冲周期T和脉冲宽度τ的变化

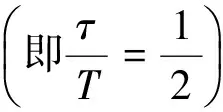
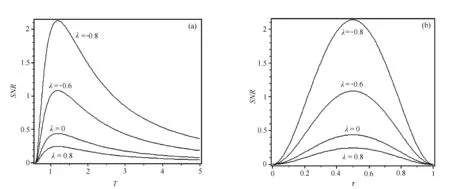
图3 信噪比SNR在不同的噪声关联系数λ值下随脉冲信号周期T和宽度τ的变化

[1]祝恒江，吴锡田. 随机共振研究进展[J].大学物理，1997，16(7)：28-31.

[2]刘立，吴大进.随机共振研究新进展[J].大学物理,2009,28(9):46-49.

[3]CAO Li, WU Dajin. Stochastic Resonance in a Linear System with Single-modelated[J].Earophys Leet, 2003,61(5):593-598.

[4]CAO Li, WU Dajin. Stochastic Resonance for Systems Driven by Correlated Noise[J].Phys Lett A, 1994,185(1):59-64.

[5]CAO Li, WU Dajin. Effects of Saturation in the Transient Process of a Dye Laser[J].Phys Rev A， 1992,45(9):6848-6856.

[6]张良英，曹力，吴大进.指数形式关联噪声驱动下单模激光线性模型的随机共振[J].中国激光，2004，31(1):53-56.

[7]张良英,曹力,吴大进.具有色关联的色噪声驱动下单模激光线性模型的随机共振[J].物理学报,2003,52(5) :1174-1178.

[8]张良英,曹力.信号调制噪声的单模激光随机共振[J].华中科技大学学报,2005,33(8):119-120.

[9]ZHANG Lingying,CAO Li,WU Dajin. Stochastic Resonance in a Single-mode Laser Driven by Quadratic Colored Pump Noise:Effects of Biased Amplitude Modulation Signal[J]. Commun Theor Phys,2009,52 (1) :143-148.

[10]ZHANG Lingying,CAO Li,ZHU Fahui. Stochastic Resonance for Signal-modulated Pump Noise in a Single-Mode Laser[J].Chin Opt Lett,2006,4(1):30-32.

[11]陈德彝,王忠龙.噪声间关联程度的时间周期调制对单模激光随机共振的影响[J].物理学报，2008,57(6):3333-3336.

[12]陈德彝,王忠龙.噪声交叉关联程度受时间周期调制下单模激光的光强关联时间[J].中国激光,2009,36(1) :119-124.

[13]陈德彝,王忠龙.色噪声间关联的周期调制对单模激光随机共振的影响影响[J].物理学报,2009,58(1):0102-0106.

[14]陈德彝,王忠龙.偏置信号调制下噪声关联的周期调制对单模激光随机共振的影响[J].物理学报,2009,58(5):2907-2913.

[15]WANG Zhiyun,Chen Peijie,ZHANG Liangyin .The effects of Sine-Squared Pulse Modulation Correlated Noises on Stochastic Resonance in Single-Mode Laser[J].Z Naturforsch A,2011,66:411-416.

[编辑] 李启栋

10.3969/j.issn.1673-1409(N).2012.04.003

O436

A

1673-1409(2012)04-N007-04

2012-02-27

国家自然科学基金项目(11045004)。

汪志云(1973-),男，1997年大学毕业，硕士，副教授，现主要从事激光动力学方面的教学与研究工作。