Picard逐次逼近法在微分方程中的应用

吴丽华 (辽源职业技术学院基础部，吉林 辽源 136201)

Picard逐次逼近法在微分方程中的应用

吴丽华 (辽源职业技术学院基础部，吉林 辽源 136201)

逐次逼近法在微分方程的求解过程中应用非常广范。证明了Picard逐次逼近法是求解常微分方程的一种有效方法，并给出了Picard逐次逼近法的应用实例。

Picard逐次逼近法；微分方程；应用

在科学领域中，几乎所有涉及到变化率的问题都能用微分方程的模型来解决。在微分方程求解的过程中，有一种证明解的存在唯一性定理的方法称为Picard逐次逼近法，它是这个定理证明的核心，也是求近似解的一个理论基础[1-2]。因此，逐次逼近法在微分方程的求解过程中应用非常广范[3-4]。下面笔者在证明其有效性的基础上举例论证其在解微分方程过程中的重要应用。

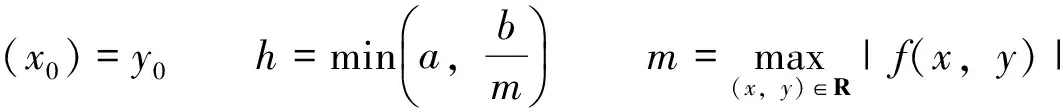
取φ0(x)=y0，构造Picard逐步逼近函数如下：

解法1(Picard逐次逼近法)f(x,y)=-2xy+4x。因为所求过(0,1)点，故可取：

……

……

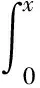
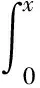
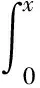
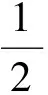
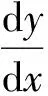
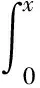
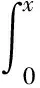
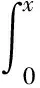
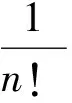
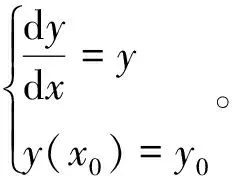
对上面近似解序列取极限值，则极限函数为所求方程的解，为：

[1]杨颖. Picard逐次逼近法的应用[J]. 吉林师范大学学报(自然科学版), 2008，29(3)：155-157.

[2] 鲜大权. 常微分方程解的存在唯一性定理教学研究[J]. 大学数学, 2009，25(6)：197-202.

[3] Liang Z. Stochastic differential equation driven by countably many Grown motions with non-Lipchitz coefficients[J]. Stochastic Analysis and Applications, 2006，24：501-529.

[4] 东北师范大学常微分方程教研室, 常微分方程[M]. 北京: 高等教育出版社, 2006.

[编辑] 洪云飞

10.3969/j.issn.1673-1409(N).2012.02.046

O175.1

A

1673-1409(2012)02-N136-02

2011-11-0

吴丽华(1969-)，女，1992年大学毕业，副教授，现主要从事数学建模方面的教学与研究工作。