基于QPSO方法的足球机器人路径规划
陆克中
(池州学院 数学与计算机科学系,安徽 池州 247000)
基于QPSO方法的足球机器人路径规划
陆克中
(池州学院 数学与计算机科学系,安徽 池州 247000)
提出了一种基于量子粒子群优化算法(QPSO)的足球机器人路径规划方法。为适应QPSO算法的自身特点和提高算法搜索的效率,在传统栅格法的基础上引入实际坐标系法,对环境进行建模;为了更好地评价粒子(即解)的性能,在进行碰撞判定的基础之上,引入罚函数方法,克服了传统适应度函数难以更好地表达粒子性能的缺点。与PSO算法的对比仿真实验表明,该算法在足球机器人路径规划方面是可行的、有效的。
量子粒子群优化算法;路径规划;足球机器人
机器人足球由加拿大不列颠哥伦比亚大学的教授Alan Mackworth在1992年的论文《On Seeing Robots》中首次提出[1],其目的是通过机器人足球比赛,为人工智能和智能机器人学科的发展提供一个具有标志性和挑战性的课题。在机器人足球赛中,路径规划作为足球机器人基本动作实现的基础,它的优劣直接影响机器人动作的实时性和准确性。因此,路径规划是机器人足球比赛的一个重要研究内容。路径规划就是在有障碍物的工作环境中,按照某一性能指标搜索一条从起始状态到目标状态的最优或近似最优的无碰路径[2]。
机器人路径规划实质上是一个有约束的优化问题。目前,各国学者对此问题已经做了大量的研究工作,这其中包括人工势场法[3]、神经网络法[4]、遗传算法[5]、蚁群算法[6]和粒子群优化算法[7]等。量子粒子群优化算法 (Quantum-behaved Particle Swarm Optmization,QPSO)是一种改进的粒子群优化算法(Particle Swarm Optmization,PSO),与 PSO 算法在量子空间中粒子满足聚集态的性质完全不同,QPSO算法可以在整个可行解空间中进行搜索,因而它的全局搜索性能优于一般的PSO算法[8]。
本研究提出了一种基于QPSO算法的足球机器人路径规划方法。首先为适应QPSO算法的自身特点和提高算法搜索的效率,在传统栅格法的基础上引入实际坐标系法,对环境进行建模;然后为了更好地评价粒子(即解)的性能,在进行碰撞判定的基础之上,引入罚函数方法,评价粒子的性能;最后利用QPSO算法实现足球机器人路径规划仿真并与PSO算法进行了比较分析。
1 QPSO算法原理
2004年,Sun等人在研究了Clerc等人关于粒子收敛行为的研究成果后,从量子力学的角度出发提出了一种新的PSO算法模型。这种模型是以DELTA势阱为基础,认为粒子具有量子的行为,并根据这种模型提出了量子粒子群算法。与在量子空间中粒子满足聚集态的性质完全不同,它可以在整个可行解空间中进行搜索,因而QPSO算法的全局搜索性能优于标准PSO算法。
在量子空间中,粒子的速度和位置是不能同时确定的,因此文献[8]通过波函数来描述粒子的状态,并通过求解薛定谔方程得到粒子在空间某一点出现的概率密度函数,随后通过蒙特卡罗随机模拟的方式得到粒子的位置方程。具体如下:
D维搜索空间中,有m个粒子,其中第i个粒子的位置是x→i=(xi1,xi2,…xiD), i=1,2,…,m。将x→i带入目标函数可计算出其适应值。记第i个粒子搜索到的最优位置为=(Pi1,Pi2,…PiD),整个粒子群搜索到的最优位置为(Pg1,Pg2,…PgD),势中心点 P(r1Pid+r2Pgd)/(r1+r2)。粒子状态更新操作如下:
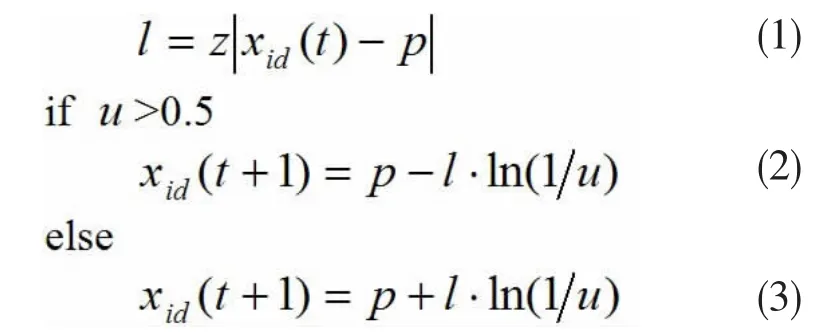
其中,i=1,2,…,m,d=1,2,…D;u,r1和 r2是介于[0,1]之间的随机数;t为当前迭代次数;z是小于的非负常数,起到收缩扩张作用,可将参数z作如下线性变化:

其中 z0,z1为常数,t为迭代步数,Tmax 为设定的最大迭代次数。
2 基于QPSO算法的足球机器人路径规划方法
2.1 环境建模
实现路径规划的前提是对环境进行描述,即对环境进行建模。建模的方法有栅格法,实际坐标系法等[8]。栅格法当规划范围较大时计算量相当大,用实际坐标系法虽然建模简单,但很难和其他成熟的规划方法结合。为了适用本文算法,且减少计算量,本文借鉴栅格法与实际坐标系法的各自优点,采用半栅格半实际坐标系法,即在横向坐标上使用栅格法,而纵向坐标上使用实际坐标系法。同时为了缩小足球机器人的搜索空间,提高搜索速度,这里将搜索范围确定为:当前机器人R,目标点G,R到G的距离为L,以L为长,L/2为宽,RG为中分线作一矩形,此矩形即为搜索空间。在矩形空间内的任何人(己方队员和对方队员)都将被看作障碍物。如图1所示,其中圆表示障碍物。

图1 足球机器人障碍环境描述与坐标变换
为了方便计算,在环境地图中建立了一个新的坐标系 X’RY’,即以 RG的连线为 X’轴,过 R且与X’垂直的直线为Y’轴。对应的坐标变换公式如下:
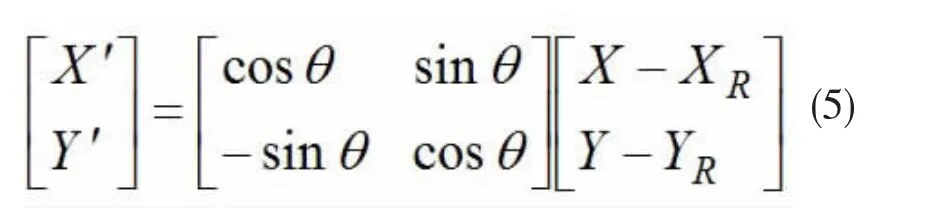
其中(X,Y)和(X’,Y’)分别为环境地图中的一点在XOY和X’RY’中的坐标,(XR,YR)为R点在XOY中的坐标。
2.2 粒子编码表示
基于上面的半栅格半实际坐标系方法,在X’RY’坐标系中,将RG线段等分m+1等份,在每个等分点作RG的垂线,垂线长度为RG/2,得到VL1,VL2,…,VLm线段,如图1所示。足球机器人从起点R沿着RG方向阶段性前进,通过调节VLi(i=1,2,…,m)上的坐标点,使得足球机器人能够寻找到一条不穿过任何障碍物 (即不与任何障碍物碰撞)的路径,如图1中的从R到G的一条S形路径。我们的目标就是找寻这样路径中长度最短的哪一条。因此粒子群算法中的粒子就是由一系列VLi(i=1,2,…,m)上的Y’轴坐标点和起止点R和G的纵坐标构成,即(0 VL1,VL2,…,VLm 0)。 这样的编码直接而简洁,且在VLi(i=1,2,…,m)上可自由移动,没有栅格法受栅格的限制,有利于粒子在解空间中搜索。
2.3 适应度函数的确定
机器人足球路径规划就是在有障碍的环境下,寻找一条由起点到目标点的路径点集合,使其构成的路径安全无碰撞,且长度最短。据此,我们将适应度函数定义为路径中各路段长度之和。对于无碰撞的路段,用其两端点之间的欧式距离表示;对于有碰撞的路段,则采取罚函数的方法,将其长度乘以一个比较大的惩罚系数,从而降低该路径的评价性能。对于有碰撞的线段通过如下步骤来判断:
计算障碍物中心点到路径线段所在直线的距离d,如果d>=r(r为障碍物的安全半径),则线段为安全线段,如图2.1所示;否则,计算障碍物中心点到路径线段所在直线的垂足,判断垂足是否在线段中间,如果是,如图2.2和2.3所示,则判断为有碰撞;否则,计算障碍物中心点到路径线段两端的距离,如果任何一端的距离小于障碍物的安全半径r,如图2.4和2.5所示,则判断为有碰撞,其它情况被认为安全无碰撞。
根据以上表述,可将适应度函数定义为:

其中fi为路段i两端点之间的欧式距离,λi为路段i对应的惩罚系数。

图2 碰撞示意图
2.4 基于QPSO的足球机器人路径规划
(1)确定粒子的维数(即RG线段的等分数m+2)和群体规模M,初始化粒子群体,在解空间范围内随机确定每个粒子的初始位置(即路径),每个粒子的初始速度设置为0。
(2)根据式(6)计算每条路径的适应度值fiti,若当前值优于Pibest,则Pibest=fiti,若在所有个体极值中,有优于 Pg的值,则 Pg=fiti。
(3)根据式(1)-(4),更新每个粒子的新位置,并把它们限制在一定范围内。
(4)t=t+1,返回到步骤(2),直到获得一个预期的适应值或t达到设定的最大迭代次数。
3 路径规划仿真
仿真环境中,足球机器人起始点R(200,150),目标点G(400,260),障碍物坐标分别是:(240,160)、(280,200)、(320,230),障碍物安全半径为 16。QPSO和PSO算法中群体规模M=20,粒子维数dim=22,最大迭代次数Tmax=400。PSO算法中学习因子c1=c2=2,惯性权重w随迭代次数的增加线性地从0.9递减到0.4。QPSO算法中,收缩扩张因子的z0=0.9,z1=0.5。仿真结果如表1所示。
表1是分别使用PSO和QPSO算法对足球机器人路径规划的30次仿真结果。从表中可以看出,由于采用了带惩罚系数的碰撞检测技术,保证了两种算法产生的所有路径都是安全无碰撞路径;从最小路径长度可见,两种算法都能够找到最优路径,最优路径如图3所示;但是QPSO算法在平均寻优性能方面明显优于PSO算法,这体现在平均路径长度等参数上,QPSO算法的平均路径长度255.56接近其最优路径长度231.98,而PSO算法的平均路径长度495.01远大于其最优路径长度232.01,这在实际应用中是非常重要的。

表1 两种算法30次路径规划仿真结果比较
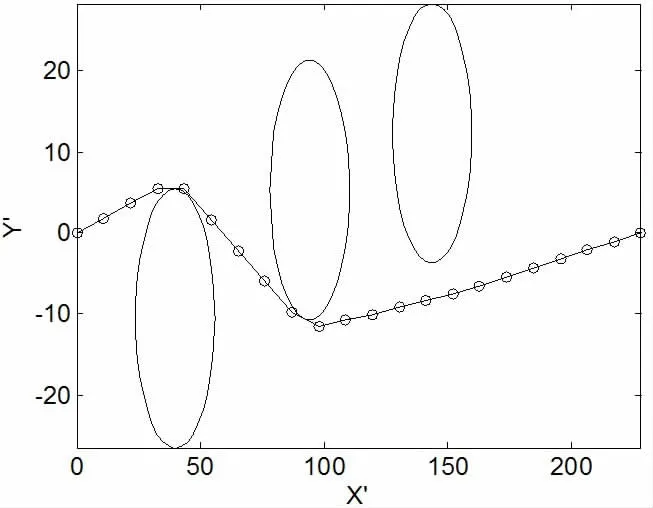
图3 最优规划路径
4 结论
本文将QPSO算法应用于足球机器人路径规划,为了适应QPSO算法的自身特点和提高算法搜索的效率,在传统栅格法的基础上引入实际坐标系法,对环境进行建模;为了更好地评价粒子(即解)的性能,在进行碰撞判定的基础之上,引入罚函数方法,克服了传统适应度函数难以更好地表达粒子性能的缺点。通过与PSO算法进行对比,仿真实验表明,该算法在足球机器人路径规划方面的可行性和有效性。
[1]Alan K Mackworth.On Seeing Robot,Computer vision:system,theory and application[M].Singapore:World Scientific Press,1993:1-13.
[2]柳长安,鄢小虎,刘春阳,等.基于改进蚁群算法的移动机器人动态路径规划方法[J].电子学报,2009,39(5):1220-1224.
[3]Derek J Bennet,Colin R McInnes.Distributed control of multi-robot systems using bifurcating potential fields[J].Robotics and Autonomous Systems,2010,58(3):256-264.
[4]邓万,郑庆,陈琳,等.神经网络极速学习方法研究[J].计算机学报,2010,33(2):279-287.
[5]刘玲,王耀南,况菲,等.基于神经网络和遗传算法的移动机器人路径规划[J].计算机应用研究,2007,24(2):264-268.
[6]华路,周之平.不确定环境下一种新的双蚁群路径规划算法[J].计算机工程与应用,2011,47(15):245-248.
[7]唐国新,陈雄,袁杨.微粒群算法在机器人路径规划中的应用[J].计算机工程与应用,2007,43(16):231-234.
[8]Jun S,Wen-bo X,Bin F.A global search strategy of quantum-behaved particle swarm optimization[C]//Proceeding of IEEE confereuce on Cybernetics and Intelligent Systems,2004:111-116.
TP242
A
1674-1103(2012)03-0009-03
2011-11-11
安徽省自然科学研究项目(KJ2011Z266);池州学院自然科学研究项目(2010ZRZ07)。
陆克中(1976-),男,安徽枞阳人,池州学院数学与计算机系讲师,硕士,研究方向为粒子群优化算法的理论及其应用。
[责任编辑:曹怀火]

