ARIMA模型在楚雄市年平均气温预测中的应用研究*
叶晓波 王 松
(楚雄师范学院计算机信息管理中心,云南 楚雄 675000)
ARIMA模型在楚雄市年平均气温预测中的应用研究*
叶晓波 王 松
(楚雄师范学院计算机信息管理中心,云南 楚雄 675000)
文章运用时间序列ARIMA模型的建模方法对云南省楚雄市1961年到2010年年平均气温进行分析研究,通过SAS软件建立了ARIMA(p,d,q)时间序列模型,同时运用建立的模型对楚雄市未来4年的年平均气温值进行了预测;本文的研究结果对当地工农业生产、人民生活具有一定参考价值。
时间序列;ARIMA;气温;SAS
1.引言
气温的变化对工农业生产、环境、水资源、人民生活有很大的影响,对气温的建模及预测一直是人工智能领域的热点话题,本文利用SAS软件对楚雄市1961年到2010年年平均气温进行分析研究,采用差分运算将原序列转换成平稳时间序列,采取ARIMA模型的建模方法对序列分析建模,从而为楚雄市年平均气温建立了ARIMA(p,d,q)时间序列模型,最后运用建立的模型对楚雄市未来4年的年平均气温进行了预测。
2.ARMA模型
一个平稳非白噪声序列是一个蕴含相关信息的序列,为提取该序列中的有用信息,通常建立一个线性模型来拟合该序列的发展,ARMA模型是目前最常用的平稳序列拟合模型;如果序列要经过差分后才是平稳非白噪声序列,就要使用ARIMA模型进行拟合。
2.1 ARMA模型
ARMA模型又称为自回归移动平均模型,是目前用来拟合平稳序列最常用的模型,它包含有三种基本形式:自回归模型AR(p),移动平均模型MA(q)和自回归移动平均模型ARMA(p,q)。通常把具有如下结构的模型称为自回归移动平均模型,简记为 ARMA(p,q):
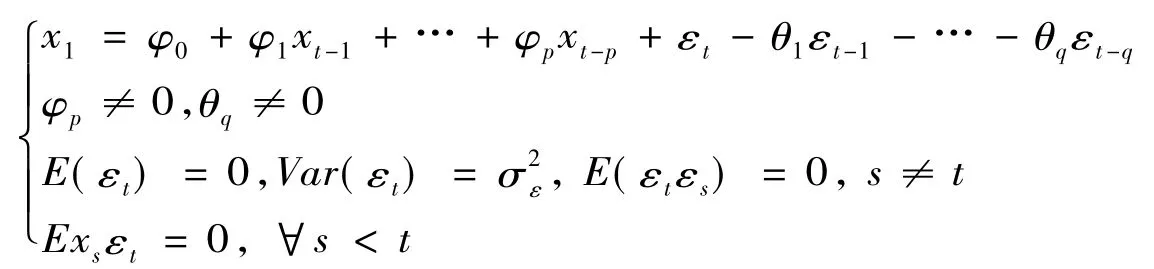
2.2 ARIMA模型
对非平稳时间序列的有用信息提取通常采用差分方法,许多非平稳序列差分后会显示出平稳序列的性质,具有该性质的非平稳序列称为差分平稳序列。对差分平稳序列可使用ARIMA模型进行拟合。
ARIMA模型又称为求和自回归移动平均模型,简记为ARIMA(p,d,q)模型,该模型具有如下结构:
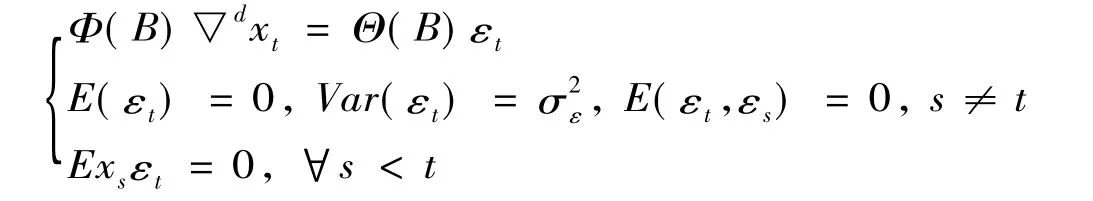
其中:
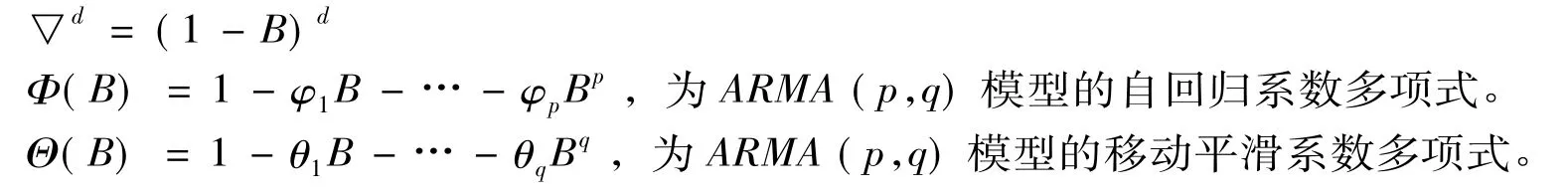
3.ARIMA模型建模过程
对一个时间序列尝试进行ARIMA模型建模时,通常按照以下步骤完成建模过程:
(1)直观检验平稳性。此步骤一般可通过绘制时间序列的时序图进行观察,如果序列的时序图显示出平稳性,就可转入下一步进行平稳性和纯随机性检验;如果序列的时序图呈现非平稳性,则可对序列使用差分运算等方法来进行进一步的处理,只有处理后的序列呈现平稳性才有可能使用ARIMA模型建模。
(2)平稳性和纯随机性检验。如果平稳序列呈现纯随机性,则说明该序列的各项之间没有任何相关关系,应该终止序列的建模工作;只有序列显示出平稳性和非纯随机性才有价值对其进行建模。
(3)模型定阶。计算序列的样本自相关系数和偏自相关系数的值,根据样本自相关图、偏自相关图和逆自相关图的性质对模型的阶数进行直观识别。
(4)参数估计及模型检验。根据模型定阶的结果,估计模型中未知参数的值,检验模型的显著性及对残差进行白噪声检验,选择最优模型。
(5)预测。使用以上步骤建立的模型对序列进行短期预测。
4.实例分析
本文选取云南省楚雄市1961年至2010年年平均气温值进行ARIMA建模,并用所建模型对楚雄市未来4年年平均气温进行预测,取得了较好的效果,下面是具体的建模预测过程:
(1)观察值序列
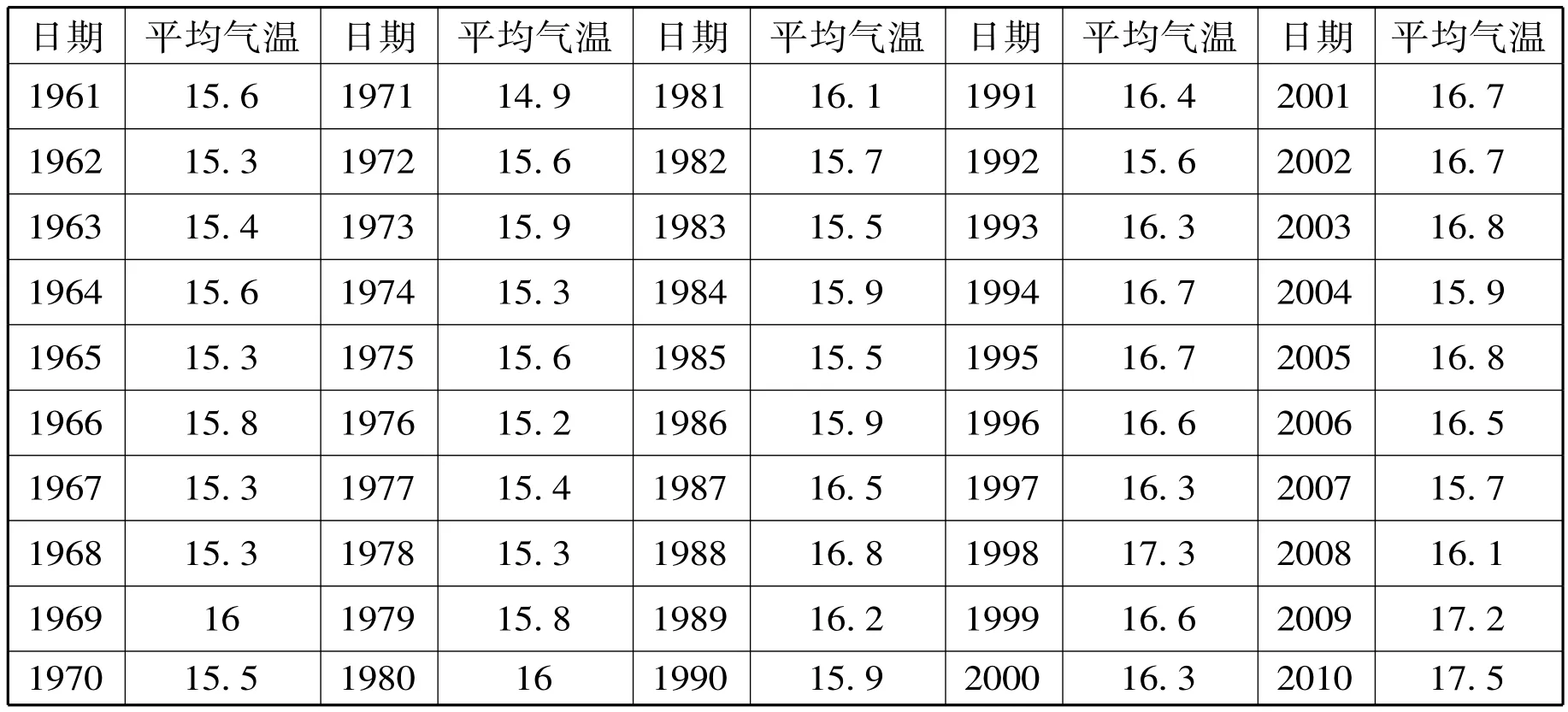
表1 楚雄市1961年—2010年年平均气温 (数据来源:楚雄州气象局)
(2)判断序列的平稳性
在SAS软件中绘制楚雄市1961年—2010年年平均气温时序图 (图1),时序图显示该序列呈现出显著的线性上升趋势,为典型的非平稳序列。根据该序列所呈现的特点,尝试对序列进行1阶差分运算并绘制差分后的时序图。图2就是对原序列进行1阶差分运算后所绘制的时序图,时序图显示出差分后序列在均值附近比较稳定的波动,直观分析原序列经过1阶差分运算后显示出平稳性。
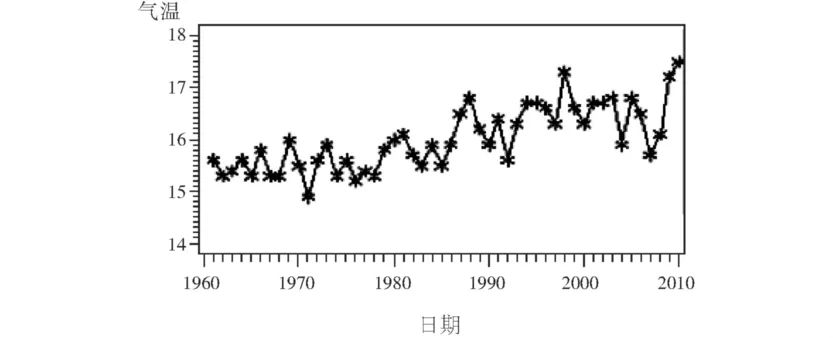
图1 楚雄市1960—2010年年平均气温序列时序图
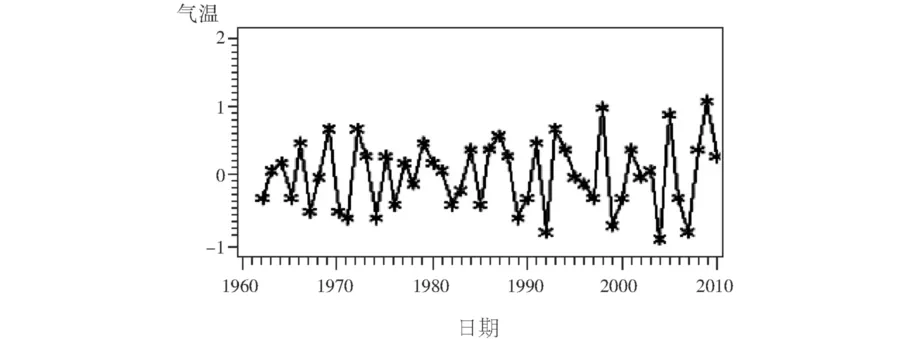
图2 楚雄市1960—2010年年平均气温1阶差分后序列时序图
(3)平稳性和纯随机性检验。
为了进一步确定差分后的序列的平稳性和序列是否属于纯随机性序列,在SAS软件中使用identify语句对差分后的序列进行平稳性和纯随机性检验,表2是检验结果:
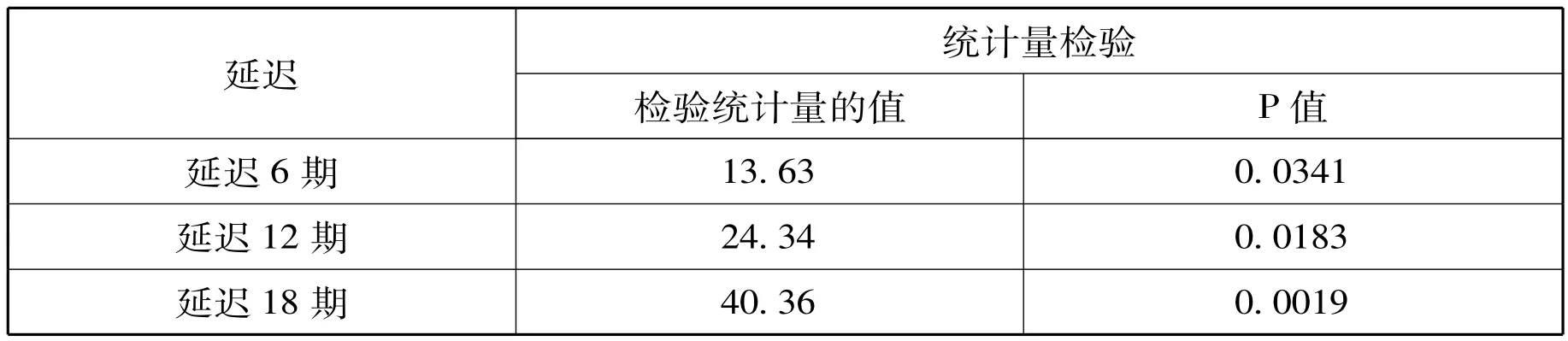
表2 序列1阶差分后纯随机性检验结果
差分后的序列纯随机性检验QLB统计量的P值均小于0.05,说明差分后该序列属于非白噪声平稳时间序列,可以进行ARIMA模型建模。
(4)模型定阶
为了确定模型的阶数,在SAS软件中使用identify语句对差分后的序列进行自相关和偏自相关图的分析,分析结果显示差分后的序列自相关图不截尾,偏自相关图除了延迟1阶、2阶和6阶的偏自相关系数显著大于2倍标准差之外,其它阶数的偏自相关系数都位于2倍标准差之内。根据自相关图和偏自相关图的特点,可尝试构造疏系数模型AR(1,2,6)。
同时,SAS系统也为建模者自动获得相对最优模型提供了方法,在identify命令中增加可选命令MINIC来获得一定范围内的最优模型定阶。在本实例中使用以下identify命令进行自动相对最优模型的选择:
identify var=x1(1)minic p= (0:7)q= (0:7)nlag=24;
图3是identify命令输出的最小信息量结果,从图3可以看出,BIC信息量相对最小的是BIC(6,0),即SAS系统分析结果认为AR(6)模型是相对最优模型。
综合考虑前面的分析结果,本例拟采用ARIMA模型和AR(6)模型对序列进行拟合。
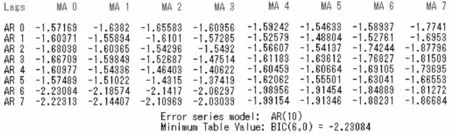
图3 identify命令输出的最小信息量结果
(5)参数估计及模型检验
在SAS软件中分别使用以下语句对AR(1,2,6)模型和AR(6)模型进行参数估计:
AR(1,2,6) 模型参数估计语句:estimate p= (1,2,6);
AR(6)模型参数估计语句:estimate p=6;
参数估计输出结果显示AR(1,2,6)模型和AR(6)模型的均值MU不显著 (t检验统计量的P值分别为0.2510和0.0581),因此在两个模型的参数估计语句后加上NOINT选项,除去常数项,再次估计未知参数的结果,表3是AR(1,2,6)模型参数估计输出结果,表4是AR(6)模型参数估计输出结果,两个模型的输出结果显示模型未知参数均显著。表5是AR(1,2,6)模型残差自相关检验结果,表6是AR(6)模型残差自相关检验结果,该统计结果显示延迟各阶的QLB统计量的P值均大于0.05,所以两个模型的残差为白噪声序列;从以上分析可知:AR(1,2,6)模型和AR(6)模型都显著成立。

表3 AR(1,2,6)模型参数估计输出结果
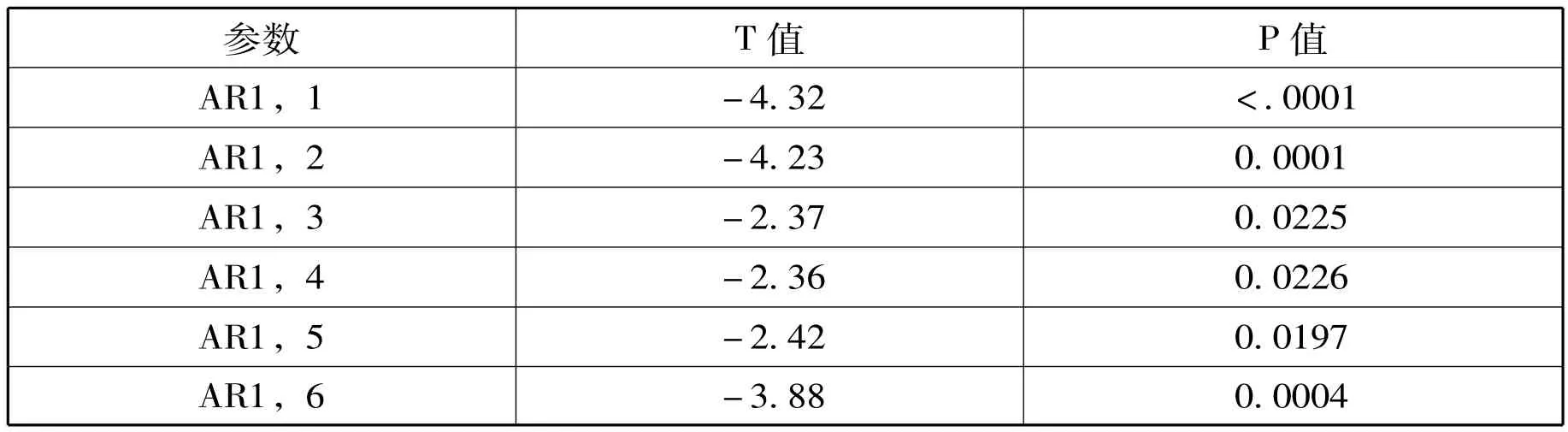
表4 AR(6)模型参数估计输出结果
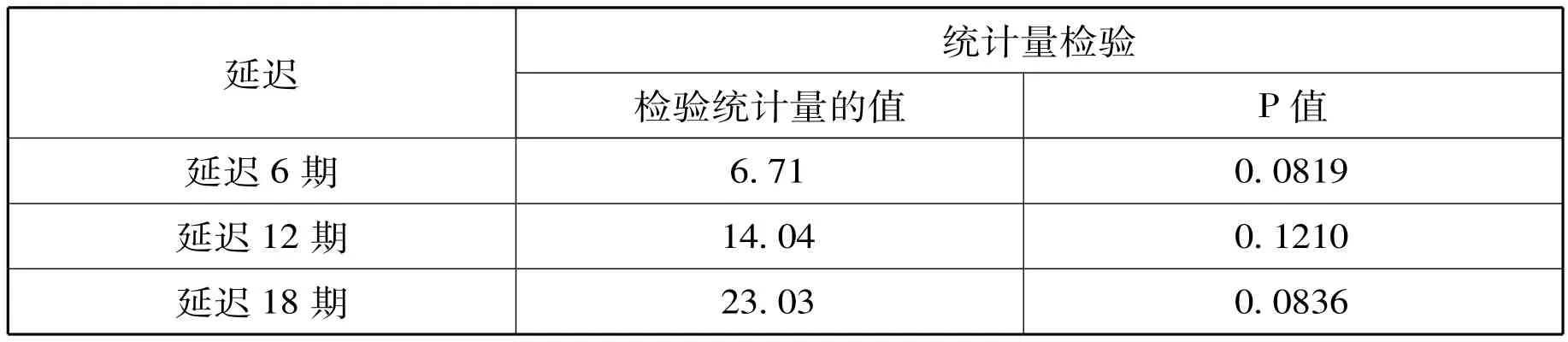
表5 AR(1,2,6)模型残差自相关检验结果
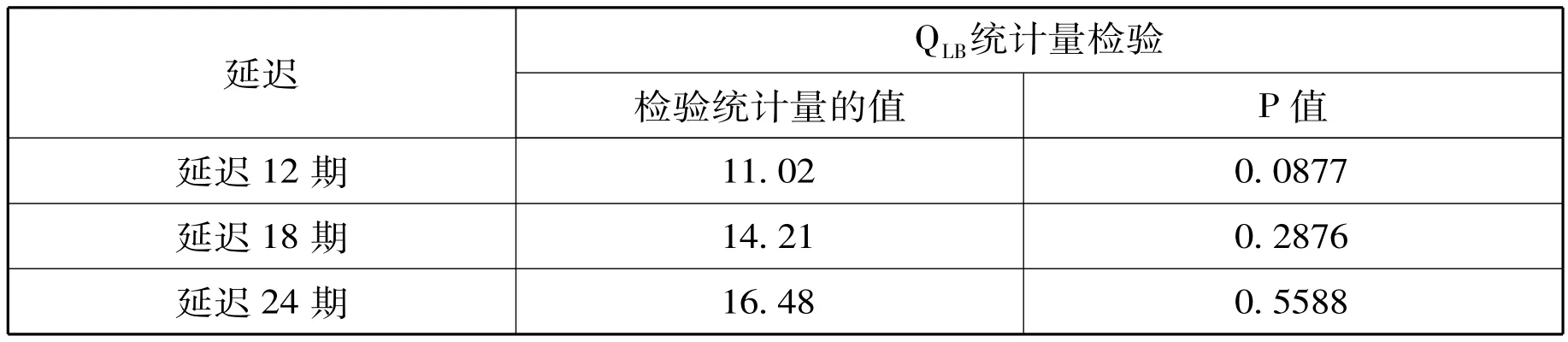
表6 AR(6)模型残差自相关检验结果
(6)选择最优模型
为了从两个显著成立的模型中找出最优模型,一般情况下使用AIC和SBC准则进行检验,能使AIC和SBC信息量最小的模型就是最优模型;表7是两个模型的AIC、SBC信息量检验结果,从表中可发现两个模型中AR(6)模型的AIC信息量较小,而AR(1,2,6)模型的SBC信息量较小,从而无法使用AIC和SBC准则进行检验;在该种情况下可参考方差估计值和标准差估计值,最优模型应该是方差估计值和标准差估计值最小的模型,根据表7中的检验结果,选择AR(6)模型为最优模型。

表7 模型的显著性参数对比
综上所述,在SAS软件中最终得到AR(6)模型为:
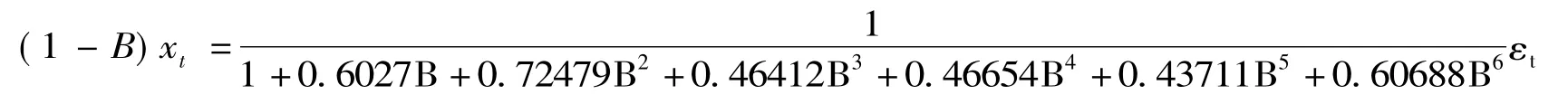
(7)序列预测
在ASA软件中使用forecast语句对楚雄市未来4年的年平均气温进行预测,预测结果如表8所示,图4是对预测结果所绘制的时序图,图中带*号的折线是原时间序列,中间不带*号的折线是预测结果,最上面和最下面的折线是95%的置信上限和下限。
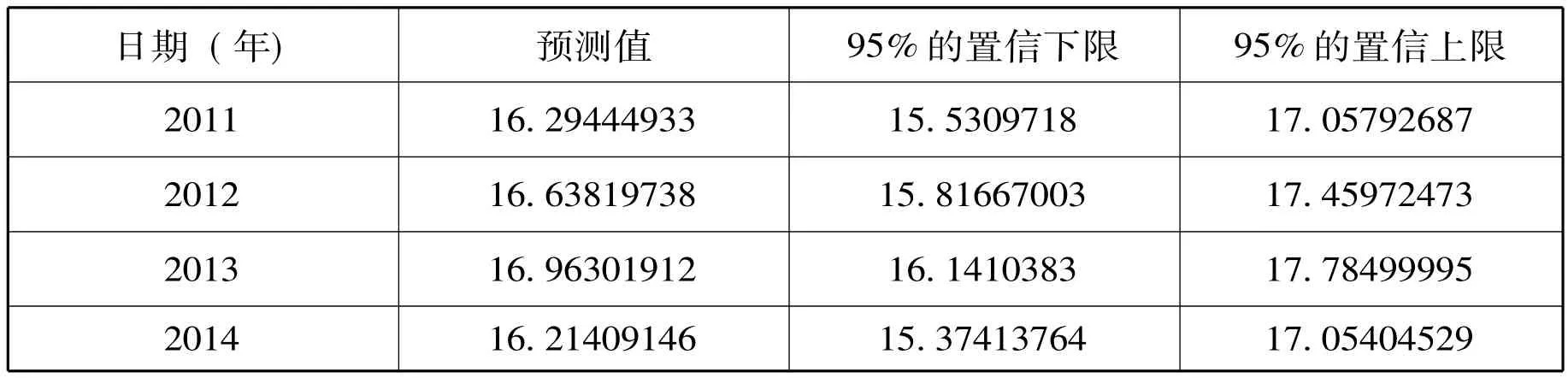
表8 楚雄市未来4年年平均气温预测结果
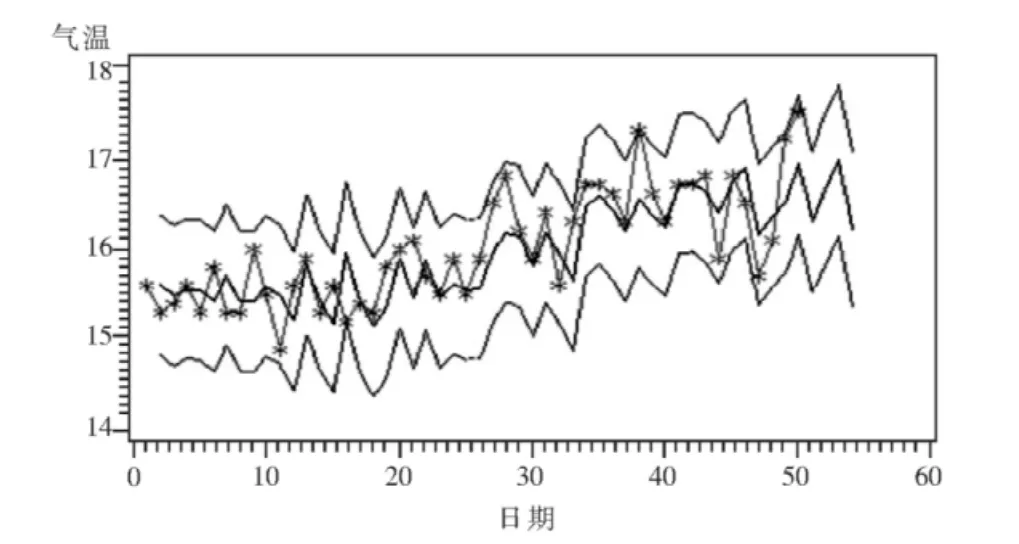
图4 楚雄市未来4年年平均气温预测结果
5.结语
从最终时间序列数据拟合结果来看,ARIMA模型对楚雄市年平均气温的拟合总的趋势是一致的,误差不大,预测值均在置信区间内,可见预测效果良好。但ARIMA模型主要适用于时间序列的短期预测,对于长期的预测方法还有待于进一步研究。
[1]王燕.应用时间序列分析 [M].北京:中国人民大学出版社,2005.
[2]孙淑珍,刘双.ARIMA模型在房屋销售价格指数预测中的应用及SAS实现 [J].湖南文理学院学报 (自然科学版).2010,22(2):1—4.
[3]王正洪,蔡蕙,蔡冠玉.基于SAS软件的城市电力需求ARIMA模型及预测 [J].现代电子技术.2007,30(2):165—167.
[4]唐玉娜,李启会.ARMA模型在预测问题中的应用 [J].嘉兴学院学报.2006,18(S1):183—187.
[5]王柏勇.鄱阳湖区永修县年季气温变化趋势预测 [J].南昌工程学院学报.2010,29(3):73—75.
The application of ARIMA model in the prediction of Annual average temperature of Chuxiong City
YE Xiao-bo;WANG Song
(The Computer Information Management Center,Chuxiong Normal University,Chuxiong 675000,China)
This paper applies modeling method of time series ARIMA model to analyze the average temperature from 1961—2010 of Chuxiong City,and to establish ARIMA(p,d,q)time series model by the SAS software.Meanwhile,using established model forecast future 4 years average temperature.This research results has certain reference value on the local industrial,agricultural production and people's life.
time series;ARIMA;temperature;SAS
TP3
A
1671-7406(2012)06-0016-06
2012-04-25
叶晓波 (1975—),男,云南大姚人,硕士,楚雄师范学院计算机信息管理中心讲师,主要研究方向:人工智能。
(责任编辑 刘洪基)

