Poisson回归模型的局部影响分析*

施红星

(楚雄师范学院初等教育学院，云南 楚雄 675000)

Poisson回归模型的局部影响分析*

施红星

(楚雄师范学院初等教育学院，云南 楚雄 675000)

本文讨论了Poisson回归模型的局部影响分析，分别针对方差加权扰动模型、响应变量扰动模型、自变量扰动模型得到了相应的影响矩阵和影响曲率的计算公式，并通过实际例子验证了本文诊断方法的有效性。

Poisson回归模型;局部影响;扰动;影响矩阵;影响曲率

1.引言

统计诊断的主要目的是判断实际数据与既定模型是否存在偏离，并指出影响点，常用的识别方法有数据删除法 (case－deletion)和局部影响分析 (local influence)。数据删除法通过比较删除数据点前后参数估计的变化大小来度量数据点的影响，进而识别影响点。局部影响分析有Cook(1986)［1］从微分几何观点提出的曲率准则方法，其基本思想是把模型扰动归结为似然函数的扰动，基于似然距离函数建立影响图，通过计算影响图的法曲率来寻找最大影响方向，研究微小扰动的局部影响。近年来，局部影响的方法在许多模型中得到广泛应用和发展，如文献［1，2］系统研究了线性模型的局部影响，文献［3—5］讨论了非线性模型及广义线性模型的情形，文献［6—8］将局部影响推广至半参数非线性模型和半参数广义线性模型的情形。对于列联表数据的局部影响分析，文献［9］有系统的研究。本文讨论Poisson回归模型的局部影响分析。

首先介绍Poisson回归模型及其极大似然估计。设(yi，)(i=1，2，…，n) 为n个数据点，β =(β1，β2，…，βP)T为 p 维未知参数，设 yi服从 Poisson 分布，其概率函数为:

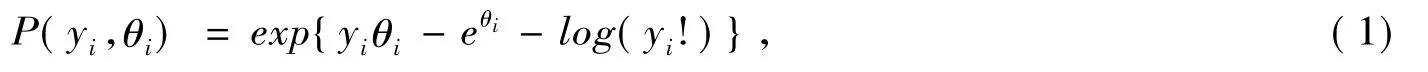
可知 μi=E(yi)=eθi，vi=Var(yi)=eθi，i=1，2，…，n。

考虑如下模型:

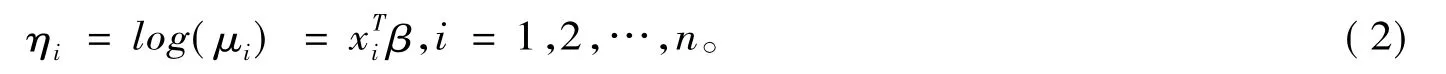
(2)式被称为Poisson回归模型，其向量形式为η=log(μ)=Xβ，其中η、μ均为n维向量，其分量分别为 ηi、μi，X=(x1，x2，…，xn)T为 n × p 矩阵，xi=(xi1，xi2，…，xip)T。

设Y=(y1，y2，…，yn)T，记Y关于β的对数似然函数为L(β)，L(β)关于β的一阶和二阶导数分别记为和，则

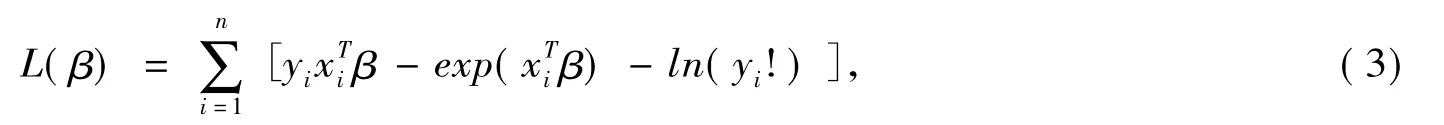
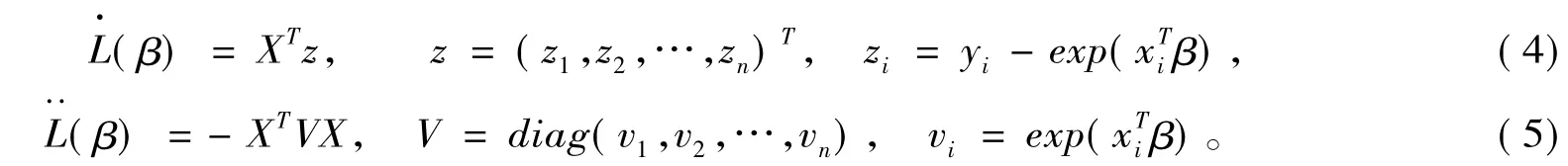
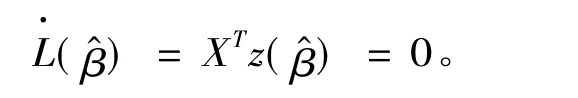
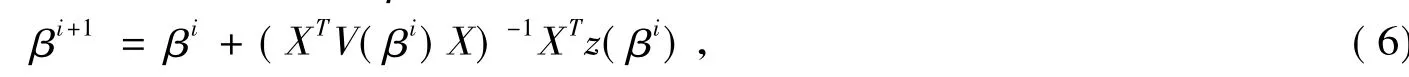
该公式可形式地表示为加权最小二乘估计的形式:

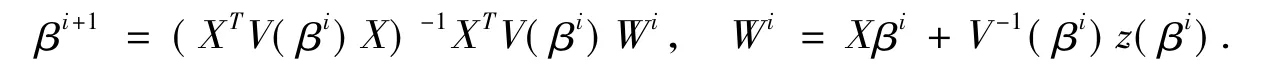
在实际应用中，取一个合适的初值β0，(6)式的迭代收敛很快。当迭代收敛时，假定，则有

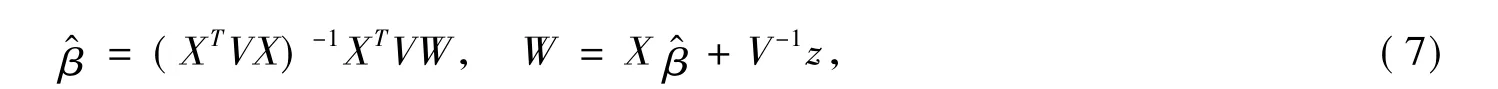
2.局部影响分析

2.1 局部影响分析的基本思想

这里首先简要介绍Cook局部影响分析的基本思想。设L(θ)为模型M相应的随机变量Y=(y1，…，yn)T的对数似然函数，θ为未知的p维参数向量，其定义域为RP的某一开子集Θ，ω=(ω1，…，ωq)T表示对模型M产生扰动的向量，其定义域为Rq的某一开子集Ω，受扰动的模型记为M(ω)，其相应的对数似然函数记为L(θ|ω)，L(θ)和L(θ|ω)的极大似然估计分别记为和。假设L(θ|ω)在Θ×Ω上存在二阶以上连续偏导数，并假定存在ω0∈Ω，使得M(ω0)=M对应于无扰动情形，因此有且定义似然距离函数为。从几何上看Z=LD(ω)表示(q+1)维空间中的一个q维曲面，用参数方程的形式表示为:

曲面(8)称为影响图，影响图随ω变化情况全面刻画了扰动对模型的影响。由于ω0对应于无扰动模型，因此影响图在ω0处的变化率反映了原模型对于扰动的敏感程度，称为局部影响。影响图(8) 在 ω0处各方向的一阶导数都为零［1，2］，Cook(1986)［1］提出借助二阶导数，利用曲率来度量影响图在ω0附近的变化情况。根据文献［1，2］可知，(8)定义的影响图在ω0处沿方向d的影响曲率可表示为:

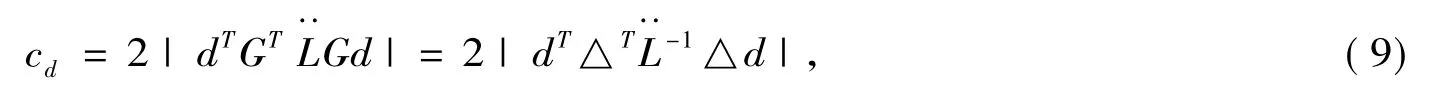
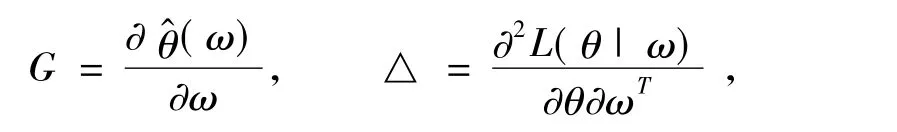
下面我们针对不同的扰动形式，利用(9)讨论Poisson回归模型的局部影响分析。

2.2 方差加权扰动模型

假定每个数据点yi的方差有扰动，ω=(ω1，…，ωn)T表示描述扰动的n维向量，ω0=(1，…，1)T表示模型无扰动，在此扰动结构下，扰动模型的对数似然函数转化为加权形式

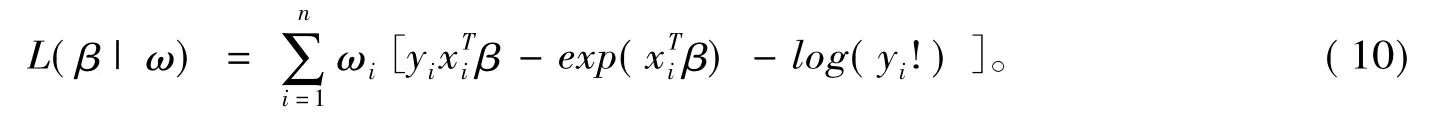
由(10)直接计算，并在(^β，ω0)处计值可得

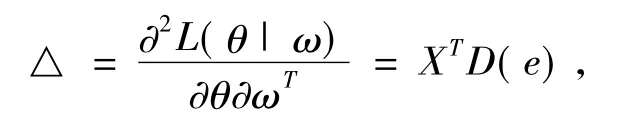
把上述结果代入(9)得到方差加权扰动模型的影响曲率计算公式为

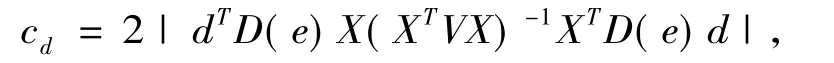
相应的影响矩阵为F=D(e)X(XTVX)－1XTD(e)，最大影响曲率表示为cmax=2λ1，λ1为影响矩阵F的特征值中绝对值最大者，最大影响曲率方向dmax为对应于λ1的特征向量。

2.3 响应变量扰动模型

响应变量的扰动也是一类常见的扰动形式。设扰动后响应变量为 Yω=Y+ω，ω=(ω1，…，ωn)T表示扰动向量，ω0=(0，…，0)T表示无扰动，在这种扰动形式下，模型的对数似然函数为

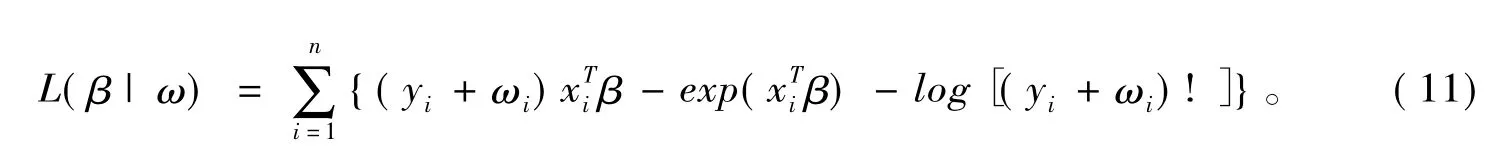
2.4 自变量扰动模型

我们研究一个自变量有扰动的情形。假定第t个自变量受到扰动，即Xt转化为Xt(ω)=Xt+ ω，其中 ω =(ω1，…，ωn)T，ω0=(0，…，0)T表示无扰动，此时，模型的分量形式化为

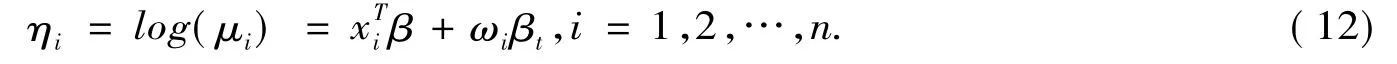
模型(12)的对数似然函数为

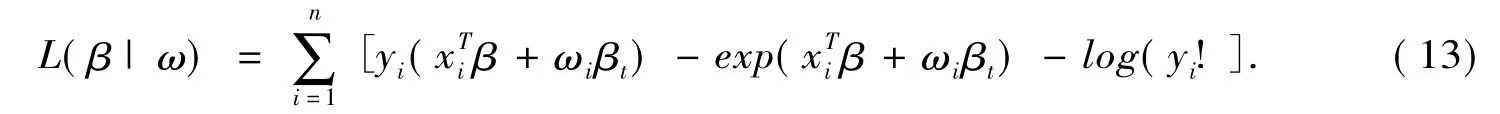
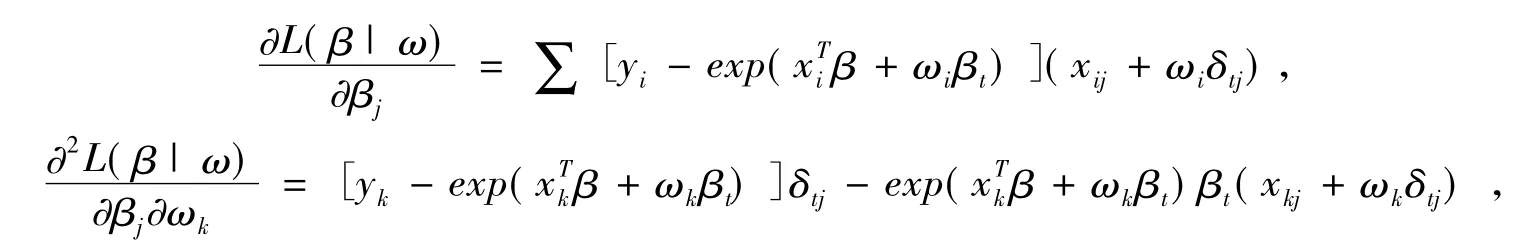
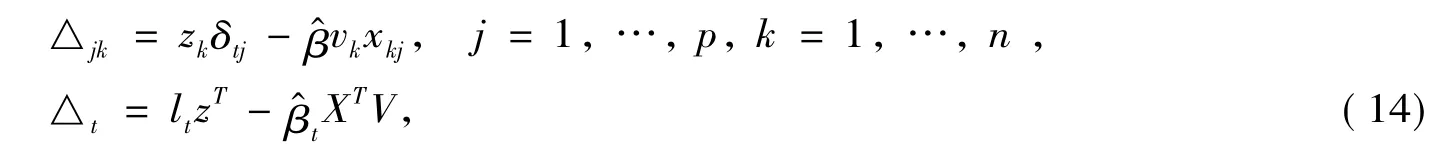
其中lt表示第t个分量为1其余分量为0的p维向量，由此得到第t列自变量受到扰动的模型的影响曲率为，影响矩阵为由(14)给出。

3.实际例子

我们以文献［10］中的数据为例，利用本文方法进行分析，说明方法的有效性。

数据为某医院在非气质性心脏病并且仅有胸闷症状的就诊者中随机收集30个患者在24小时中的早搏数y，研究早搏与吸烟x1、喝咖啡x2和性别x3的关系。

其中y表示24小时内的早搏数，x1=1表示吸烟，x1=0表示不吸烟，x2=1表示喜欢喝咖啡，x2=0表示不喜欢喝咖啡，x3=1表示男性，x3=0表示女性。

对于该实际例子，我们采用前面的回归模型和算法，通过三次Gauss－Newton迭代算法的计算，得到

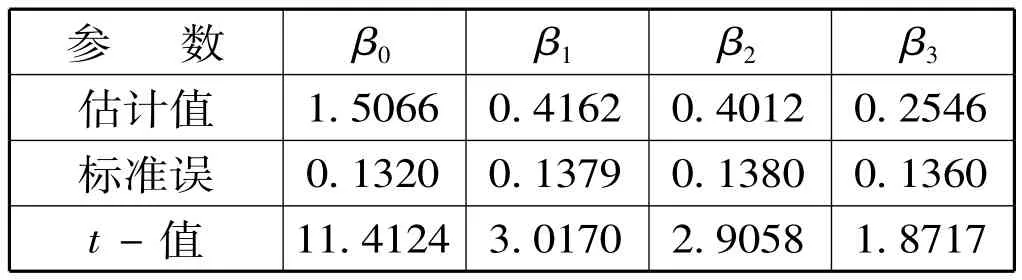
表一 参数估计值

由于本例子的自变量均是哑变量，讨论自变量扰动的模型没有实际意义，因此我们只进行前两种扰动模型的局部影响分析。在上述参数估计的基础上，分别计算基于方差扰动模型和响应变量扰动模型的各样本点局部影响统计量如下表二。

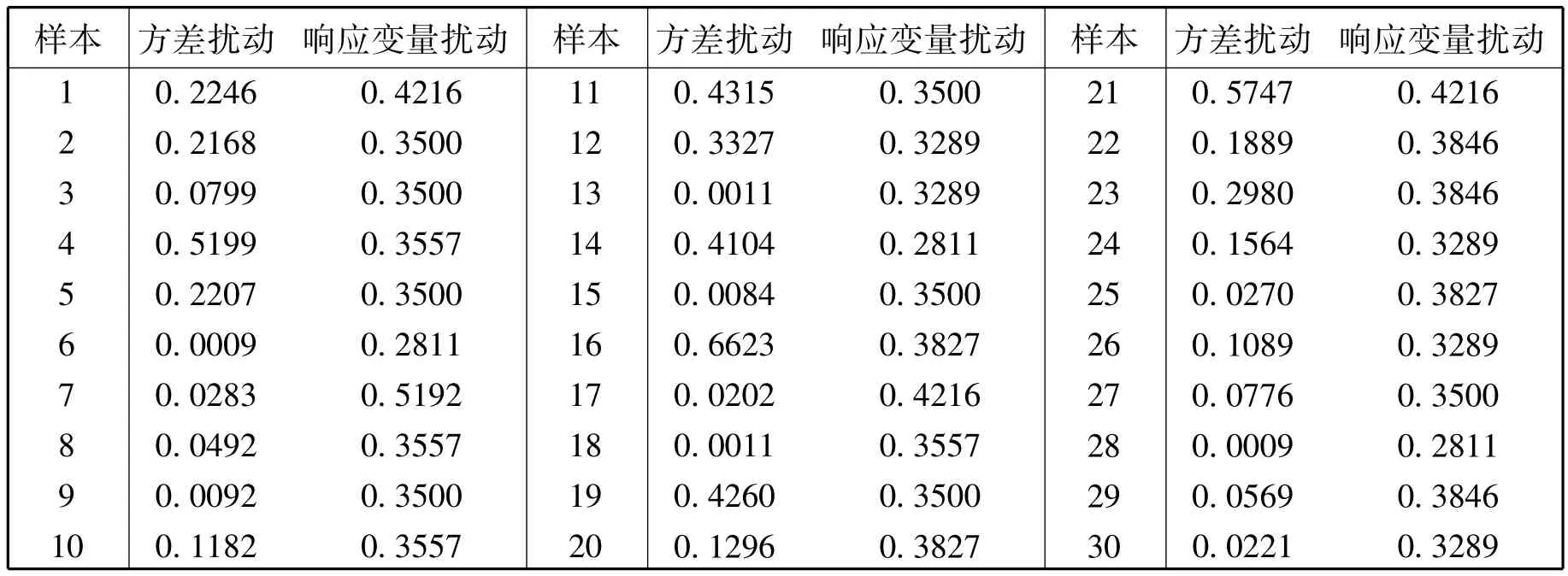
表二 两类扰动方式的局部影响统计量结果

由此可知相应的局部影响统计量图为

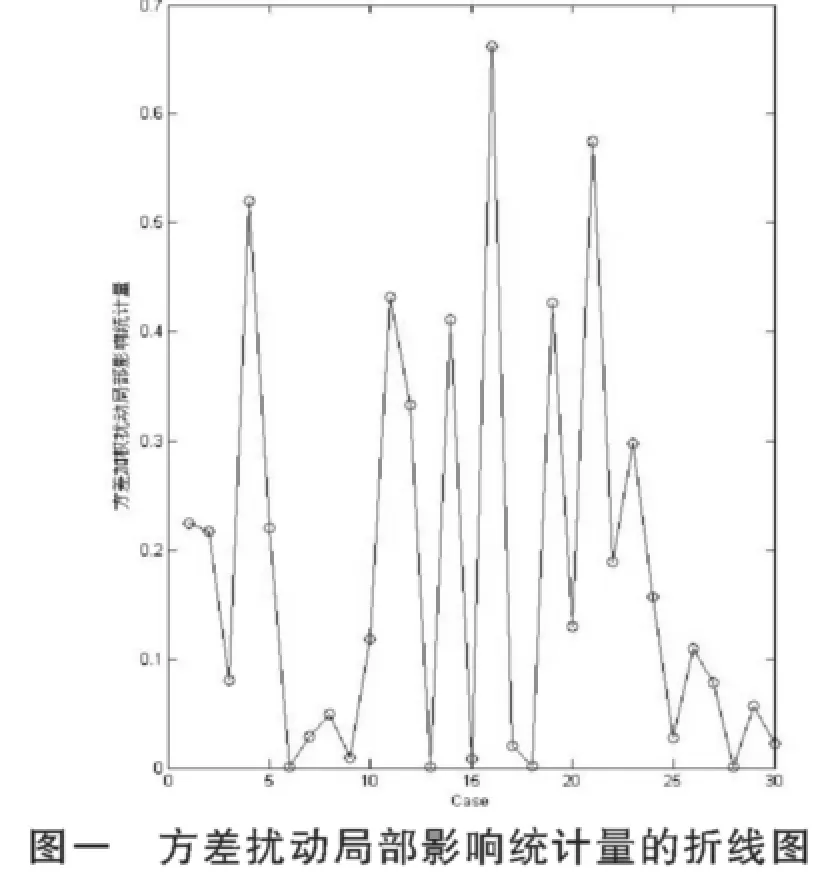
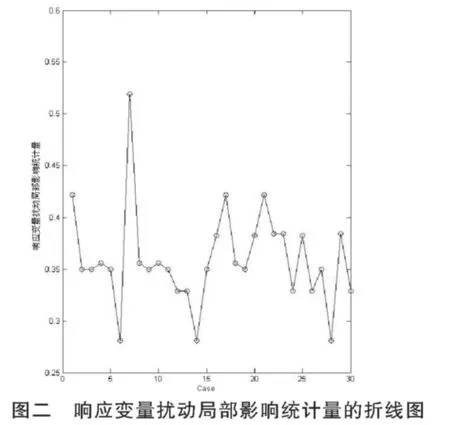
从方差扰动的局部影响统计量的折线图可以发现，第16号，21号，4号是强影响点，其次是第11号，14号和19号，这与广义Cook距离和得分函数SCi关于样本点的变化具有大致相同的趋势(//［11］);但从响应变量扰动的局部影响统计量来看，则第7号是最强影响点，其次是第1号，第17号和第21号，这与前一种扰动的结果就有很大的不同，也与广义Cook距离和得分函数SCi的发现有很大的不同，值得进一步关注和分析。

［1］ Cook R D.Assessment of local influence ［J］ .J R Statist Soc B，1986，48:133—169.

［2］韦博成，鲁国斌，史建清.统计诊断引论 ［M］.南京:东南大学出版社，1991.

［3］Thomos W，Cook R D.Assessing influence on regression coefficients in generalized linear models ［J］.Biometrika，1989，76:741—749.

［4］ Wei B C.Expenential Family Nonlinear Models［M］ .Sinapore:Springer－Verlag，1998.

［5］Green P J，Silverman B W.Nonparametric Regression and Generalized Linear Models［M］.London:Chapman and Hall，1994.

［6］朱仲仪，韦博成.半参数非线性模型的统计诊断与影响分析［J］.应用数学学报，2001，24(4):568—581.

［7］曾林蕊，朱仲仪.半参数广义线性模型的局部影响分析［J］.华东师范大学学报(自然科学版)，2005，4:18—25.

［8］曾林蕊，朱仲仪.半参数广义线性随机效应模型的影响分析［J］.数学物理学报，2007，27A(4):584—593.

［9］何利平，石磊.列联表数据的局部影响分析 ［J］.数学物理学报，2011，31A(2):518—527.

［10］峁诗松.统计手册 ［M］.北京:科学出版社，2003.

［11］施红星.Poisson回归模型的统计诊断与影响分析 ［J］.云南师范大学学报 (自然科学版)，2009，29(5):34—38.

Local Influence Analysis for Poisson Regression Model

SHI Hong－xing
(School of Primary Education，Chuxiong Normal University，Chuxiong 675000，China)

This paper studies the local influence for Poisson regression model．The counting formulas of influence curvature and influence matrix for case－weights perturbation model，mean shift perturbation model and arguments perturbation model are obtained．Finally the numerical example illustrates that the method is effective．

Poisson regression model;local influence;perturbation;influence matrix;influence curvature．

O212.1

A

1671－7406(2012)06－0005－05

云南省教育厅科研基金项目 (06Y027A);楚雄师院科研基金项目 (05－YJYB01)

2012－02－27

施红星 (1970—)，男，云南楚雄人，副教授，理学硕士，主要研究方向:应用统计。

(责任编辑 李艳梅)