隧道围岩流变参数的粘弹性位移反演与验证

李德海

（厦门地质工程勘察院，福建厦门 361008）

隧道围岩流变参数的粘弹性位移反演与验证

李德海

（厦门地质工程勘察院，福建厦门 361008）

将解析反演和数值反演相结合，对试验毛洞的断面形状和所处应力场做出适当的简化，利用对应性原理求解出洞室位移的Kelvin粘弹性解，并以此去拟合试验洞不同位置处的实测位移而得到多组流变参数;分别将其作为FLAC3D数值模型蠕变模式的输入参数，得出各自对应的实际断面形状和实际应力场条件下试验洞的蠕变位移数值解。然后，利用BP神经网络，对各组流变参数和其对应的试验洞同一位置处的蠕变位移数值解进行训练，建立起两者之间的非线性关系;利用训练好的网络，依据实测蠕变位移值得出了围岩流变参数;最后，利用隧道实测位移数据对反演的流变参数进行了数值正分析验证。

隧道;围岩;流变;粘弹性位移;反分析;数值模拟

0 引言

由于尺寸效应和工程因素的影响，用室内蠕变试验确定的岩样的流变参数往往与隧道围岩本身的流变参数存在一定的差别，因此不能直接将其作为数值计算的输入参数。20世纪70年代发展起来的反分析法在某种意义上不仅具有消除岩样尺寸效应等因素影响的作用，而且由于实测物理量包含了工程因素的影响，使得以反分析所获取的流变参数进行实际工程岩体的流变分析能取得与现场较为一致的预测结果。位移反分析是目前反分析方法中应用最多的一种。对于流变问题，即是在反演的过程中，以现场流变试验毛洞的蠕变位移为实测物理量去获取围岩的流变参数，其方式可分为2种:解析反演和数值反演。文献［1～3］利用解析反演的方法，通过隧道蠕变位移解析解或由其推出的蠕变柔量拟合出流变参数。文献［4～6］则采用了数值反演的方法给出了围岩流变参数值。然而两种方法均有其缺点:解析反演只适用于简单几何形状和边界条件下的线弹性、线粘弹性和无支护隧道问题;而数值反演则可能会因为量测数据的离散性而陷入计算不收敛的困境，即便收敛，也可能会因为模型复杂，节点多而迭代时间过长。因此如何用反分析的方法迅速有效地获取断面形状和应力条件复杂的隧道围岩流变参数是一项有意义的探讨工作。本文提出的在简化条件下用解析反演得出的结果作为耦合BP神经网络的FLAC3D数值反演迭代初值的方法，可迅速有效地反演出围岩的流变参数。

1 静水压力下圆形洞室的Kelvin粘弹性位移解

Kelvin模型是由弹簧和粘壶并联而成的流变元件模型（图1），它是典型的可用于描述衰减蠕变的粘弹性模型，其蠕变曲线见图1。鉴于试验洞实测蠕变位移都是随时间趋于稳定的衰减型曲线，因此本文选用Kelvin模型对试验洞的粘弹性位移进行解析。

图1 Kelvin流变模型及其蠕变曲线

根据对应性原理，粘弹性问题的解可根据相应的弹性问题的解通过Laplace正逆变换获得［7］。对于静水压力状态下的圆形洞室，由开挖引起的圆形洞室无支护径向位移为［8］:

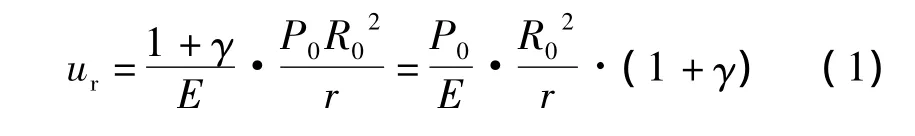
式中:E——弹性模量;γ——泊松比;R0——圆形洞室半径;r——计算点距离圆心的距离;P0——地应力。

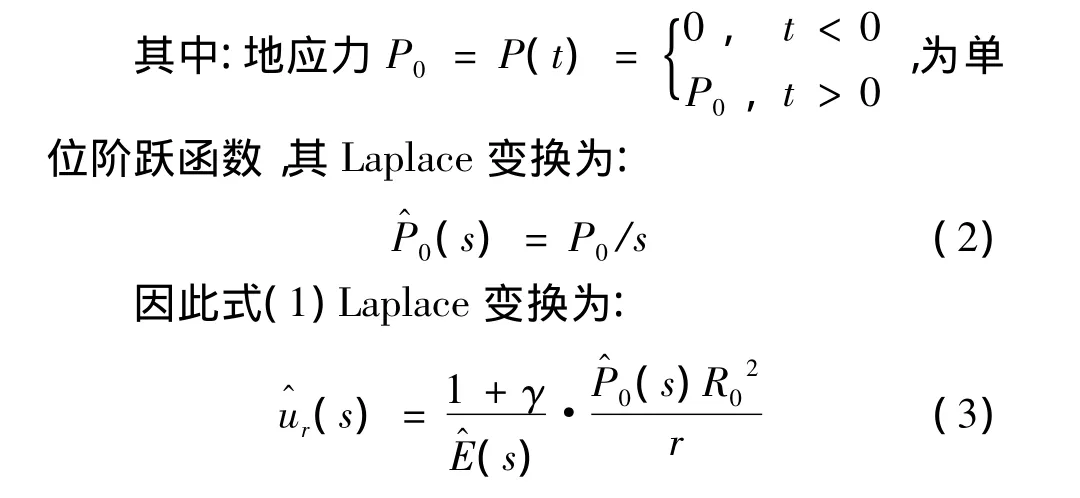
对于Kelvin模型，流变本构方程为:

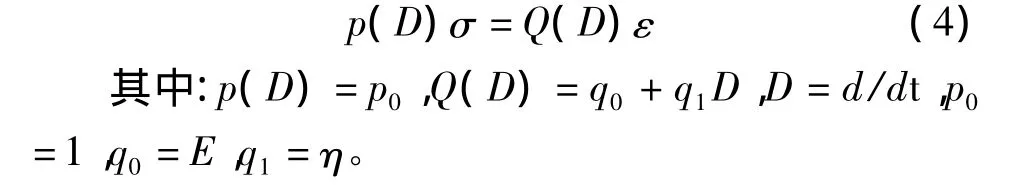
式中:D——对时间的微分算子;η——Kelvin模型的粘滞系数。

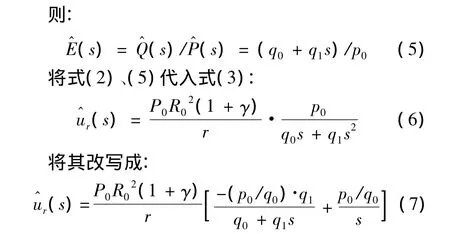
查Laplace逆变换表，对其进行 Laplace逆变换:

将p0=1，q0=E，q1=η代入，并考虑到弹性模量和剪切模量的关系E=2G（1+γ），得洞室相应于Kelvin模型的粘弹性无支护径向位移为:

对于洞壁，r=R0，代入上式即可得洞壁处的粘弹性无支护径向位移为:

2 试验洞FLAC3D数值模拟方案

2.1 概述

在某隧道中开挖两条横洞，分别称为左横洞和右横洞，并将其作为流变试验洞。为了获取围岩的蠕变变形，采用如下的FLAC3D数值模拟方案:（1）模拟初始地应力场，并将相应的初始位移场清零;（2）模拟试验洞开挖，得到开挖后的应力场，并将相应的由开挖引起的位移场清零;（3）打开蠕变计算模式，模拟试验洞的蠕变变形，获取相应的蠕变位移场。

2.2 实测初始地应力

试验洞所处地应力环境为:最大水平主应力SH为14～17 MPa，垂直于试验洞轴线方向;最小水平主应力Sh为8～9 MPa，平行于试验洞轴线方向;用上覆岩层重力估算的垂直应力SV为4～5 MPa，故模拟过程中最大、最小水平主应力和垂直应力的方向分别为x，y和z方向，如图2所示。

2.3 试验洞FLAC3D模型建立

试验洞为直墙拱顶形式的断面，跨度和高度均为2 m。依据隧道开挖的影响范围，计算边界取为上下左右边界距离拱的圆心均为6 m。另外，按平面应变计算，沿隧道轴向取为0.1 m，网格划分如图2，模型共划分246个单元，节点数506。

图2 试验洞FLAC3D计算模型

位移边界条件为:按平面应变计算，隧道轴向无位移，左右边界受水平方向的位移约束，下边界受竖向位移约束。同时，为了模拟初始应力场，左右边界受构造应力的面力作用，上下边界受重力的面力作用，边界内部受重力体力作用。

2.4 蠕变变形前的应力场模拟

试验洞开挖前要先模拟初始地应力场。选用摩尔-库仑弹塑性本构关系，计算参数为:围岩密度ρ=2000 kg/m3，力学参数按照现场大剪试验选取:弹性模量E=5.762×109Pa，泊松比μ=0.3，粘聚力c=2.1 ×105Pa，内摩擦角 φ =27.5°，抗拉强度 2.63×106Pa。在FLAC3D中，采用体积模量K和剪切模量G，按下式计算:

模拟的试验洞初始地应力场见图3。由图3可知，初始垂直地应力为4～5 MPa，水平地应力为14～15 MPa，与实测值基本一致。

图3 初始地应力云图

在试验洞开挖之后、蠕变变形之前，还要模拟试验洞开挖后经过瞬时弹塑性变形后的应力场。采用相同的本构模型和计算参数，可得到模拟的开挖后应力场，见图4。

3 试验洞围岩流变参数的粘弹性位移反分析

3.1 蠕变变形监测点布置

图4 开挖后应力云图

为了量测试验洞围岩的蠕变变形，在试验洞洞壁上布置洞周收敛和拱顶下沉监测点，布置图见图5。对3个测点采用电子全站仪测定三维坐标，然后换算出收敛及沉降变形，且认为监测到的变形仅为蠕变变形，而不包含开挖后的瞬时变形。在建立的FLAC3D模型中，记录相应的拱顶、拱脚位置处节点的竖向和水平位移，如图6。

图5 试验洞测点布置图

图6 试验洞模型中记录位移的节点位置

3.2 BP神经网络训练样本确定

3.2.1 输出样本——流变参数的确定将式（10）改写成:其中试验洞的等效半径按下式计算［9］:

式中:R0——等效隧道开挖轮廓半径;h——断面高度;B——隧道开挖轮廓跨度之半。

计算得试验洞等效半径为1667 mm。

根据式（11），分别对左、右横洞的拱顶沉降、左右拱脚沉降和拱脚水平收敛用origin进行拟合，即可得到8组BP神经网络输出样本。左、右横洞的实测时态变形曲线见图7和图8。拟合的流变参数见表1。

图7 右横洞开挖后90天内实测变形曲线

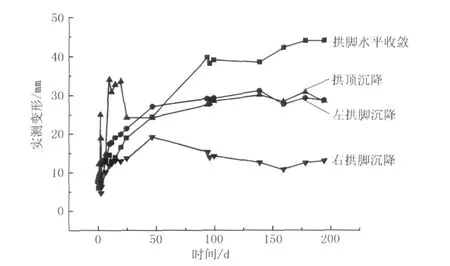
图8 左横洞开挖后90天内实测变形曲线

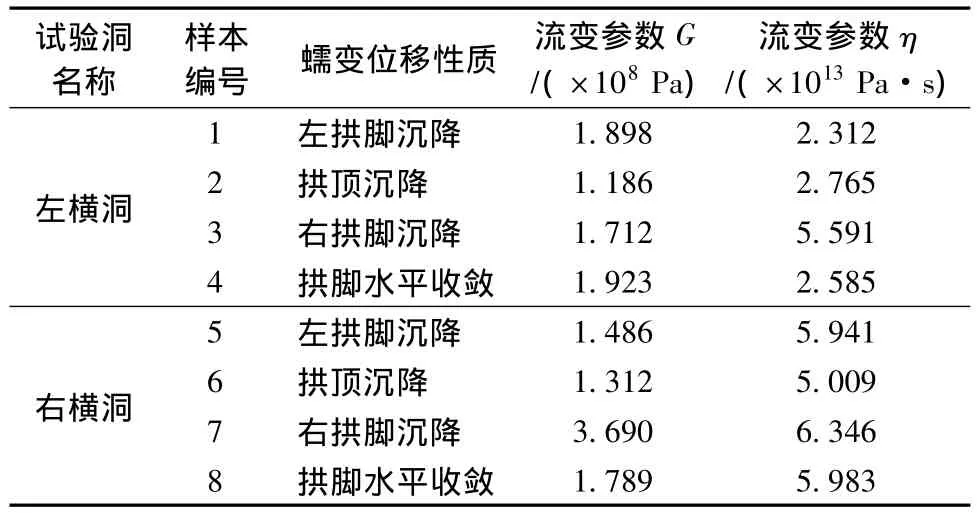
表1 拟合的流变参数

根据第3节得出的FLAC3D模型（应力场为试验洞开挖并发生瞬时弹塑性变形后的应力场，位移场清零），打开蠕变计算模式，选用Burgers流变本构模型，其中Maxwell部分的mshear和mviscosity不予赋值，Kelvin部分的kshear和kviscosity分别赋予表1中的8组G和η值，密度ρ仍取为2000 kg/m3，体积模量K仍取为4.8×109Pa，边界条件不变，控制参数取为 lfob=1.0e-3，ufob=5.0e-3，lmul=1.01，umul=0.9，时间步取值按下述原则选取:（1）最大时间步maxdt≤η/G;（2）最小时间步mindt比maxdt小2～3个数量级;（3）初始时间步dt=mindt。按此原则所取的各组样本的时间步见表2。同时开启时间步的自动调整功能，分别求取各组样本对应的第10、20和90天的拱顶沉降蠕变变形，提取图6中的节点1、2、3的垂直位移和节点2、3的水平位移，得到各组输出样本对应的输入样本，见图9。

表2 各组样本蠕变计算中时间步取值

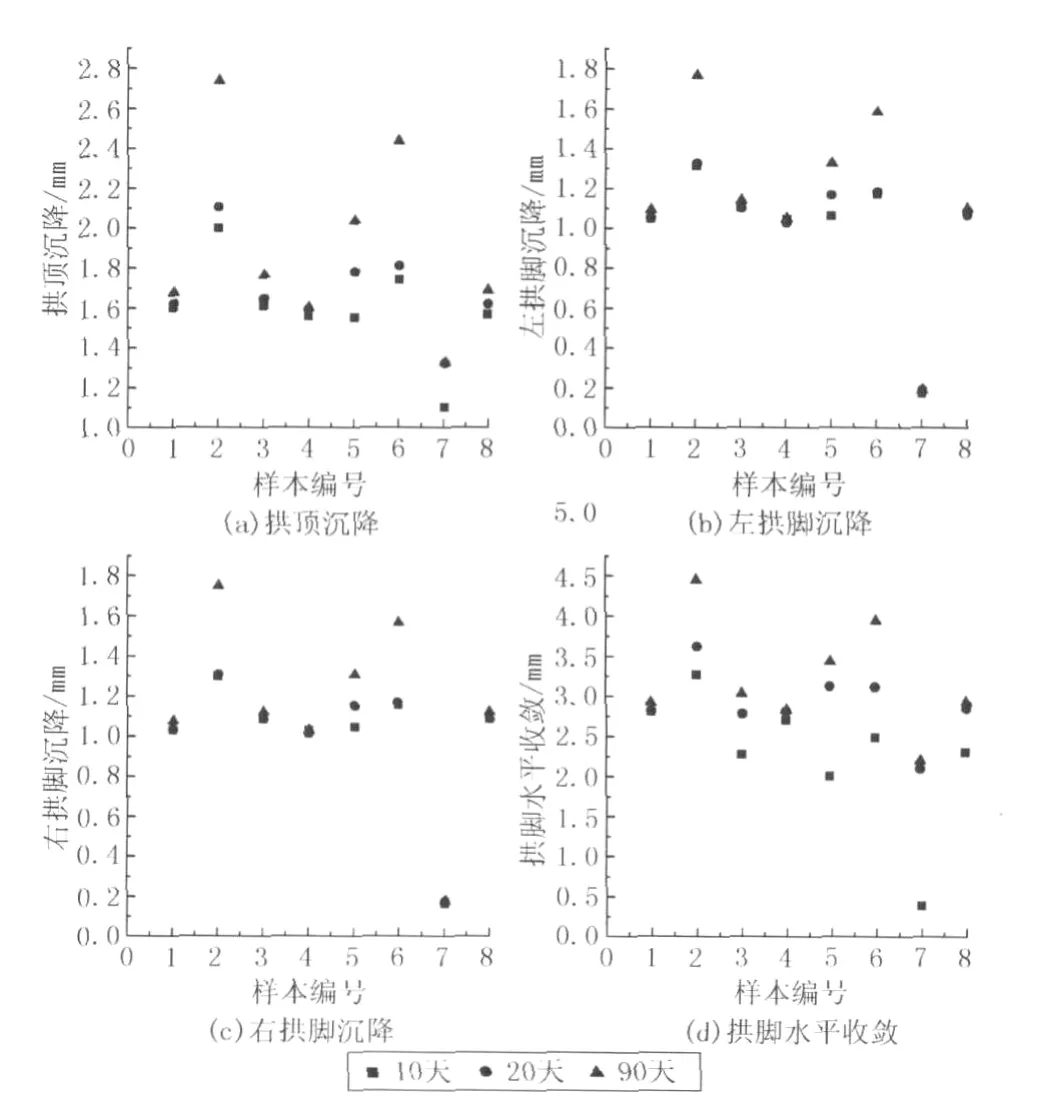
图9 输入样本——蠕变位移

3.2.2 输入样本——拱顶沉降蠕变变形的确定

限于篇幅，只给出第二组样本对应的拱顶位置处历时90天后的沉降蠕变曲线，见图10。

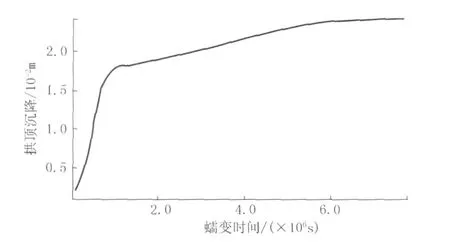
图10 拱顶沉降蠕变90天内蠕变曲线

3.2.3 神经网络反演围岩的流变参数

用BP神经网络对样本进行训练以获取输入输出样本之间的高度非线性映射关系的技术已经较为成熟。限于篇幅，本文不对BP神经网络进行详述，其工作原理参见文献［10］。

比较图7和图8可知，右横洞的实测变形历时曲线更好地表现出了围岩衰减蠕变的特性，其曲线形式与数值计算的结果吻合，故首先选用右横洞的拱顶沉降实测变形反演围岩的流变参数。

神经网络的结构计算参数对最终的训练结果有很大的影响。以图9（a）数值计算的拱顶第10、20和90天的沉降值为实际输入，以与之相应的试验洞流变参数为实际输出，分别对其进行归一化处理并将处理结果转置后分别作为输入层与输出层，这是因为考虑到BP网络输入层节点数不至于过多以及输出矩阵和输入矩阵应具有相同的列数（8列）。经过反复调试，当取隐含层节点数r=8、学习速率η=0.45、训练步数t=2000时，训练的效果较好。训练结束的时候，共经历了2000步运算，此时训练误差为3.98×10-15，符合要求。训练过程的误差曲线见图11。整个过程借助于MATLAB 7.0完成。网络训练好以后，以图7中实测的拱顶沉降为实际输入，经过反归一化后即可反演试验洞围岩的流变参数，反演结果见表3。

图11 BP神经网络训练误差曲线

类似地，可以右横洞的左拱脚沉降、右拱脚沉降和拱脚水平收敛为输入样本，输出样本仍取表1的值，对其进行训练，将实测蠕变位移输入各自训练好的网络，即可得出反演的流变参数，见表3。

表3 反演的流变参数

反演结果表明，对于Kelvin模型，可认为其剪切模量G在1.19×108Pa附近，粘滞系数η在（2.5～6）×108Pa·s之间。

4 反演结果的数值正分析验证

某隧道轴线与试验洞轴线垂直，断面形式为曲墙拱顶仰拱式，其跨度为7.66 m，高度为8 m，依据隧道开挖的影响范围，计算边界取为:左右边界距斜井断面竖直中轴线20 m，上下边界距斜井断面拱圈圆心所在水平面20 m。另外，按平面应变计算，沿隧道轴向取为1 m。网格划分如图12，模型共划分1680个单元，节点数2541。

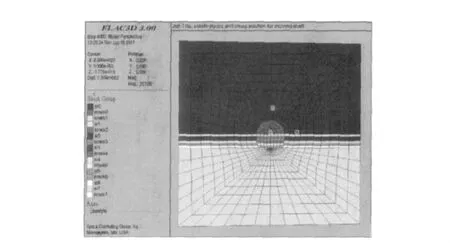
图12 隧道FLAC3D计算模型

在建立的FLAC3D模型中，记录图13所示节点的水平位移，计算相应的拱脚及墙腰位置处的水平收敛，并与实测的斜井拱脚及墙腰水平收敛对比，以验证反演流变参数的合理性。

采用相同的数值模拟方案，仅需在应力边界中将水平构造应力改为Sh=8 MPa。在获得隧道开挖后经过弹塑性变形的应力场后，打开蠕变计算模式，根据上节反演的流变参数，取流变参数均值，即kshear=1.19 ×108Pa，kviscosity=3.76 ×1013Pa·s，并考虑随着计算蠕变时间的不同，采用变时间步dt，见图14。其他计算参数和控制参数不变，计算所得的拱脚和墙腰蠕变收敛值与实测值对比见图15和图16。

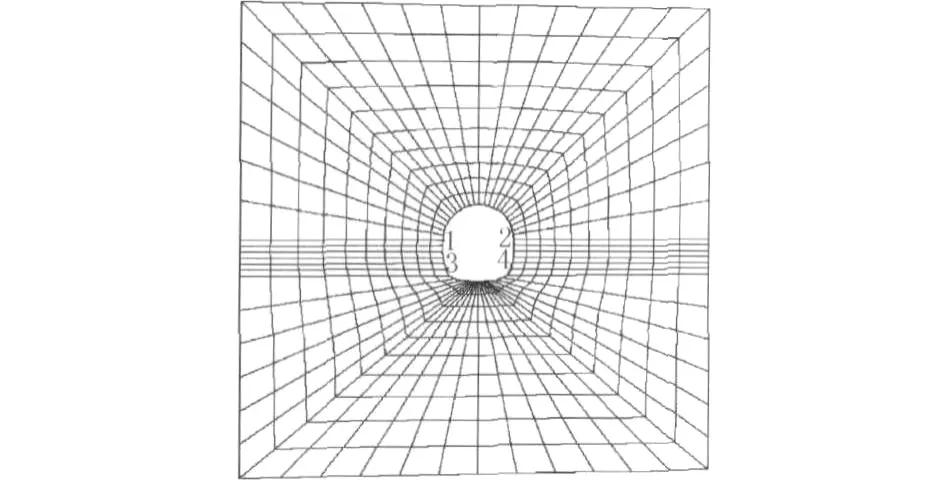
图13 隧道模型中记录位移的节点位置

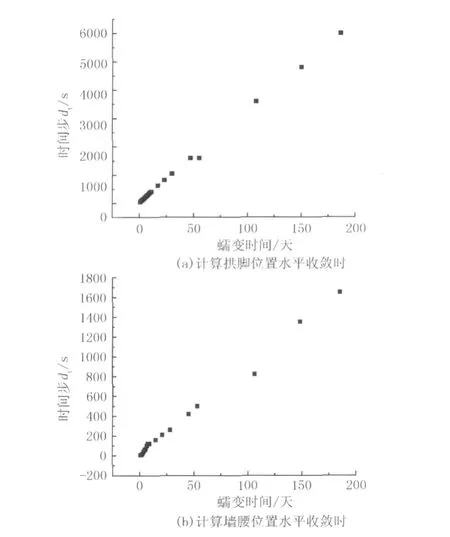
图14 蠕变时间步取值

图15 拱脚水平收敛实测值与数值正分析值对比图

5 结论

图16 墙腰水平收敛实测值与数值正分析值对比图

根据对应性原理，推导了圆形洞室在静水压力状态下的Kelvin粘弹性位移解析解，用此解析解初步反演得出简化条件下的围岩流变参数，并将其作为耦合BP神经网络的FLAC3D数值反演迭代初值，一方面避免了迭代初值选取的随意性，给出了一种有效的神经网络样本确定方法，另一方面也加快了数值反演的速度和反演结果的精确性。将反演的结果用于数值正分析验证，结果与实测值吻合的很好，表明了该方法是合理的，能够用于断面形式和应力条件复杂的隧道围岩流变参数反分析。

另外，在使用FLAC3D蠕变模式模拟隧道蠕变变形时，计算所取的时间步与蠕变时间为线性关系时模拟的效果较好，可为以后的研究提供借鉴。

［1］ 薛琳.圆形隧道围岩蠕变柔量的确定及粘弹性力学模型的识别［J］.岩石力学与工程学报，1993，12（4）:338-344.

［2］ 刘世君，徐卫亚，邵建富.岩石粘弹性模型辨识及参数反演［J］.水力学报，2002，（6）:101-105.

［3］ 赵旭峰，孙钧.挤压性软岩流变参数反演与本构模型辨识［J］.铁道工程学报，2008，（5）:5-8.

［4］ 李云鹏，王芝银.粘弹性位移反分析的边界元法［J］.西安矿业学院学报，1989，9（1）:17 –24.

［5］ 陈炳瑞，冯夏庭，丁秀丽，等.基于模式–遗传–神经网络的流变参数反演［J］.岩石力学与工程学报，2005，24（4）:553-558.

［6］ 杨有海，王长虹.考虑时空效应的隧道工程黏弹性位移反分析［J］.地下空间与工程学报，2005，5（3）:468-472.

［7］ 周光泉，刘孝敏.粘弹性理论［M］.安徽合肥:中国科学技术大学出版社，1996.

［8］ 罗佑荣，唐辉明.岩体力学［M］.湖北武汉:中国地质大学出版社，1999.

［9］ 王中文，方建勤，夏才初，等.考虑围岩蠕变特性的隧道二衬合理支护时机确定方法［J］.岩石力学与工程学报，2010，29（S1）:3241-3246.

［10］ 崔志盛，金磊，赵凯.双向八车道连拱隧道围岩力学参数反演分析［J］.探矿工程（岩土钻掘工程），2011，38（5）:65-69.

Back Analysis and Verification on Rheological Parameters of Tunnel Surrounding Rock through Visco-elastic Displacement

LI De-hai（Xiamen Geological Engineering Investigation Institute，Xiamen Fujian 361008，China）

Based on the correspondence principles，the analytical visco-elastic solution of round tunnel displacement under hydrostatic pressure is given using Kelvin constitutive law.After simplifying the testing tunnel as a round one subjected to hydrostatic pressure，the preliminary rheological parameters are obtained by using the analytical solution to fit the monitoring displacement data.A FLAC3Dmodel is then established in which the testing tunnel is of the real shape and is under the real ground stress.The preliminary rhelogical parameters are then adopted as parameters required under the creep option of FLAC3D，and the numerical solution of the test tunnel displacement is then given.With the help of BP neural network，the mapping relationship between the rheological parameters and the corresponding numerical solution of displacement are established.And the rheological parameters are then back analyzed by applying monitoring data to this trained network.Finally，the verification of the usefulness and reliability of the back-analyzed rheological parameters is given by implementing a normal calculation process to a tunnel.

tunnel;surrounding rock;rheology;visco-elastic displacement;back analysis;numerical simulation

U45

A

1672-7428（2012）02-0074-06

2011-08-03

李德海（1977-），男（汉族），福建漳平人，厦门地质工程勘察院工程师、国家注册岩土工程师，岩土工程专业，从事工程勘察、岩土设计的工程技术和管理工作，福建省厦门市莲前西路192号，282588020@qq.com。