基于Plaxis 强度折减法的开挖边坡稳定分析

吴丽君

(湖南城市学院土木工程学院，湖南益阳 413000)

0 引言

边坡稳定分析一直是岩土工程中的重要研究课题。目前，边坡稳定的分析方法已有数十种，主要可分为两大类:第一类可称作传统方法，如极限平衡法、滑移线法等;第二类为基于计算机技术的数值分析方法，如有限元法、边界元法等。第一种方法在工程上使用较多且已有大量研究证明了其实用性和准确性，因此我国相关的工程设计规范推荐的方法为建立在极限平衡理论基础上的极限平衡法，包括瑞典圆弧法、Bishop法、Morgenstern-Price法、Spencer法等。而随着计算机技术和有限元理论的发展，数值分析方法在工程实际中得到广泛的应用［2］，有广阔的发展前景。本文将首先针对Plaxis有限元强度折减法的基本原理做简单介绍，然后采用有限元强度折减法针对一开挖高边坡分别对无支护措施和采用预应力锚索加固两种方案进行稳定分析，并将结果与极限平衡法得到的结果进行比较。

1 Plaxis有限元强度折减法原理

1975年Zienkiewicz等人［7］首次在弹塑性有限元数值方法中引入了强度折减系数概念而发展了土坡稳定分析的强度折减弹塑性有限元方法。其基本原理体现在进行有限元弹塑性计算时，首先对于某一假定的强度折减系数Fs，将土的强度参数c，tanφ同时进行折减，通过逐级加载的弹塑性有限元数值计算来确定边坡内的应力场、应变场或位移场，并且对应力、应变或位移的某些分布特征以及有限元计算过程中的某些数学特征进行分析，根据一定的失稳判据确定边坡达到极限平衡状态，则与此相对应的强度折减系数就是总体安全系数。在大型岩土工程软件Plaxis程序中强度折减有限元法同样表现为对强度参数tanφ和c不断折减直到计算模型发生破坏。Plaxis程序中系数∑Msf定义为强度的折减系数，其表达式为:

其中，tanφinput和cinput为程序在定义材料属性时输入的强度参数值;tanφreduced，creduced为在分析过程中用到的经过折减后的强度参数值。∑Msf按设置的数值递增至计算模型发生破坏后趋于一常值，反映在位移与安全系数关系曲线上就是曲线基本水平，此时的∑Msf为模型的安全系数值。

2 开挖边坡稳定分析

2.1 工程概述

边坡场地基岩为志留系砂质页岩，按风化程度可分为强风化砂质页岩和中等风化砂质页岩。边坡几何尺寸及有限元模型如图1所示。上层岩体为强风化页岩，容重为23 kN/m3，粘聚力c=30 kPa，内摩擦角为 20°;下层岩体为中风化页岩，容重为26 kN/m3，粘聚力 c=40 kPa，内摩擦角为 30°。

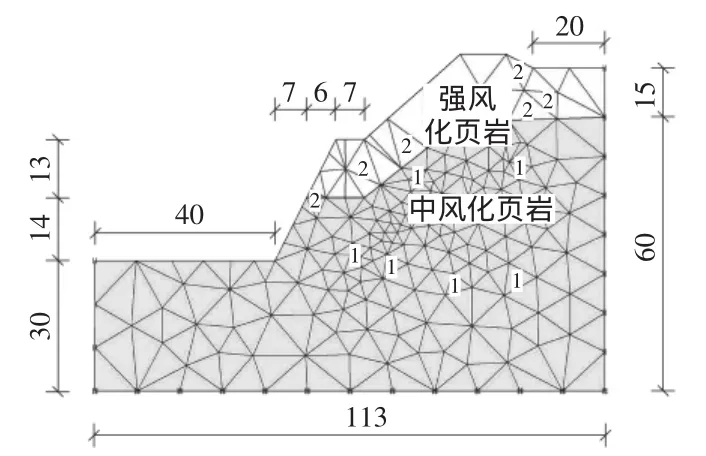
图1 边坡几何尺寸及有限元模型（单位：m）

2.2 有限元模型的建立

利用Plaxis程序进行平面应变分析，采用平面6节点单元对模型进行自动网格划分。计算中，土的本构模型均采用基于摩尔—库仑屈服准则和非关联流动法则的理想弹塑性模型，剪胀角ψ=0°。边坡计算区域的底面采用固定约束，左右两侧面均为水平约束，其他为自由边界。计算只考虑岩体自身重力作用的稳定分析。

关于如何考虑岩体自身重力作用，Plaxis程序通过设置边坡有限元模型的初始条件(即初始应力场)来实现。Plaxis程序可以通过K0法和施加重力荷载两种方法考虑初始应力场的影响。本文在施加初始应力场时采用的是施加重力荷载的方法，重力加速度取为 9.8 m/s2。

2.3 结果分析

考虑边坡安全系数可能小于1，采用有限元强度折减法稳定分析时折减系数不能以1为起点开始增加，因此将强度参数c和tanφ分别放大2倍后再用有限元强度折减法进行计算，边坡临界失稳时得到最大的折减系数为1.686，因此边坡安全系数Fs=1.686/2［1］，即为 0.843，而极限平衡 Bishop 法得到的安全系数为0.862，误差约为2%。有限元强度折减法得到的边坡潜在滑裂面如图2所示。

从图2可知，边坡潜在的危险滑裂面位于强风化岩层，且靠近两层岩体的边界。图3为极限平衡Bishop法得到的最危险滑裂面。比较图2与图3可知，两种方法得到的潜在滑裂面形状和位置基本一致。

结果表明，该边坡存在滑坡危险，需采取削坡减载或加固措施。由于本例边坡属于高边坡，削坡减载方案需要改变边坡坡率，这样将使征地范围变更较大，开挖土方量也较大，因此考虑采用锚索加固措施。

图2 有限元强度折减法得到的边坡潜在滑裂面

图3 极限平衡Bishop法得到的边坡潜在滑裂面

3 锚索加固边坡稳定分析

考虑采用预应力锚索加固，每根锚索施加预应力1 500 kN，水平排距4 m，角度为向下倾斜10°，锚索的抗拉刚度为3.461×105kN，坡面和坡体上共布置8排，如图4所示。考虑到锚索须穿过无支护边坡的潜在滑裂面，所以图4中1号锚索长设为15 m，2号锚索长为20 m，3号锚索长为25 m，4号锚索长为30 m。

图4 预应力锚索加固边坡模型

经过强度折减有限元稳定分析，得到边坡的安全系数为1.313，满足规范要求;与极限平衡Bishop法得到加固后边坡的安全系数1.304相比，误差仅为0.69%。边坡潜在滑裂面位置分别如图5，图6所示。

4 结语

本文通过Plaxis有限元强度折减法对开挖边坡的稳定分析，得到如下结论:

图5 预应力锚索加固后强度折减法边坡潜在滑裂面

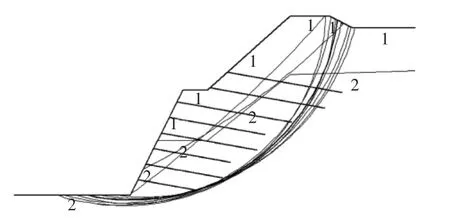
图6 预应力锚索加固后极限平衡Bishop得到的边坡潜在滑裂面

1)Plaxis有限元强度折减法用于开挖边坡的稳定分析，其计算得到的安全系数与极限平衡Bishop法计算结果相比，误差在2%以内，且两种方法得到的危险滑裂面形状和位置基本一致，证明了Plaxis有限元强度折减法用于边坡稳定分析的准确性和可行性。

2)与边坡加固前相比，采用预应力锚索对边坡加固以后，边坡的安全系数明显提高，有较大的安全储备，可以满足设计和规范要求，其最危险滑裂面往边坡下部岩层移动，边坡趋于更加稳定。

［1］吴丽君.有限元强度折减法有关问题研究及工程应用［D］.长沙:中南大学硕士学位论文，2009:51-66.

［2］刘柞秋，周翠英，董立国，等.边坡稳定及加固分析的有限元强度折减法［J］.岩土力学，2005，26(8):558-561.

［3］Bishop A.W.The use of the slip circle in the stability analysis of slope slopes［J］.Geos technique，1955(5):7-17.

［4］郑颖人，赵尚毅，张鲁渝.用有限元强度折减法进行边坡稳定分析［J］.中国工程科学，2002，4(10):57-78.

［5］张建勋，陈福全.用强度折减有限元法分析土坡稳定问题［J］.山东科技大学学报(自然科学版)，2004，23(1):115-117.

［6］李佳雨桐，侍克斌，严新军.基于Plaxis强度折减法的土石坝坝坡稳定分析［J］.水利科技与经济，2012，18(8):30-32.

［7］Zienkiewicz O C，Humpheson C，Lew is R W.Associated and non-associated visco-plasticity and plasticity in soil mechanics［J］.Geostechnique，1975，25(4):671-689.

［8］程 哗，赵明华，曹文贵.基桩下溶洞顶板稳定性评价的强度折减有限元法［J］.岩土工程学报，2005，27(1):38-41.