基于小波变换的车门运行模态分析
王超峰, 林建辉
(西南交通大学牵引动力国家重点实验室,四川成都 610031)
0 引言
高速列车在行驶过程中,一般受到轨道不平顺、轨道变形、风载荷以及车轮踏面等造成的激励。而且在两车交会或是在进出隧道时,可能会在车体表面形成峰值很高的瞬态压力波[1]。这些激励都会对车门构件带来很大的安全影响。所以,对高速列车车门进行模态分析是结构优化设计与结构损伤检测基础,具有十分重要的意义。
高速列车运行过程中,在车门的响应存在的非平稳的随机信号、有局部断点的信号及一些不能用傅里叶变换来分析的信号,可以利用小波变换将信号分解到不同尺度,以达到模态自动解耦的效果。
1 模态分析基础理论
模态分析实质上是一种坐标的线性变换,将振动系统以物理坐标和物理参数所描述的、互相耦合的运动方程组,能够变为一组彼此独立的方程(每个独立方程只含一个独立的模态坐标)[2-3]。
经过离散化处理后的多自由度系统,它在物理坐标系统中的运动微分方程实际上为结构动力学模态分析中的特征值问题。一个n自由度系统的运动微分方程为:

对该方程进行变换可得:

此为一个广义特征值问题。对于n自由度系统,求解该方程便可确定ωn和{φn},即特征解,其中特征值ω1, ω2,…, ωn代表系统对应的n个固有频率(正交模态)。当结构振动时,它在任何时候的运动都是正交模态的线性组合。
2 基于小波变换的模态识别
对多自由度黏性阻尼振动系统自由振动响应作小波变换:

由于小波变换为线性变换,可以交换上式积分和求和的顺序,同时将Ai(t)。
在t=τ附近的泰勒级数展开[4]并忽略无穷小量,得到:

不同的尺度下的小波变换相当于用一组带通滤波器对信号进行带通滤波处理[5],选择不同的尺度参数,使小波基的频窗中心近似等于某阶模态频率,这样就实现了模态滤波和系统解耦。所以,解耦后的各独立模态的小波变换可表示为:

根据上式,多自由度系统黏性阻尼系统自由振动响应信号经过小波变换后[6],由其模及相位可以得到:

系统第i阶振型在某一时刻t=τt每一个自由度的自由振动响应的小波变换系数,从而可以得到该多自由度系统的第i阶振型[7-8]为:

对i取不同的值即可得到不同阶的振型。
3 实例分析
现对某一型列车车门进行运行模态分析。测试系统包括美国National Instruments(NI)公司的数字采集器2个,型号为NI16255,精度级为±0.1%;Lance(朗斯)公司的加速度计12个,型号为LC0711A,精度级为±0.5%;采用可视化编程的LabVIEW对数据进行显示。通过便携式笔记本电脑,实时观测数据采集情况。利用手持式GPS测定客车的运行速度。
在车门处布置12个加速度传感器,具体布置如图1所示。

图1 车门测点布置
测点5测试结果经过随机减量法处理后的连续小波变换谱图如图2所示。
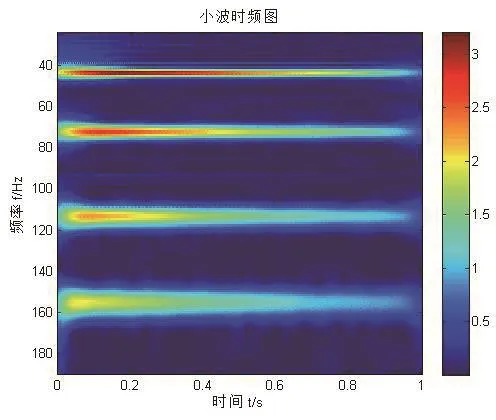
图2 小波谱图
从图2可以看出,谱图上的4条脊线分别对应车门的前四阶频率。而且,随着时间推移,小波脊线上的系数的能量逐渐减小,这与信号是自由振动衰减响应的情况是一致的。通过读取相应的脊线在所对应频域的位置,即可得到车门的前四阶模态频率为:42.8 Hz,76.8 Hz,112.1 Hz,162.2 Hz。
车门前两阶归一化振型分别如图3、图4所示。
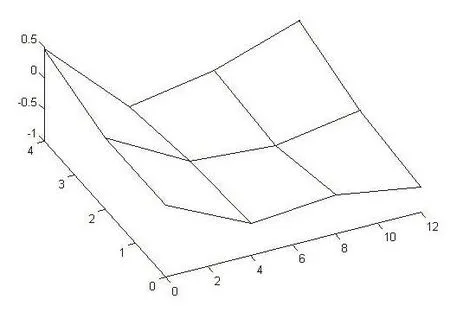
图3 第一阶振型
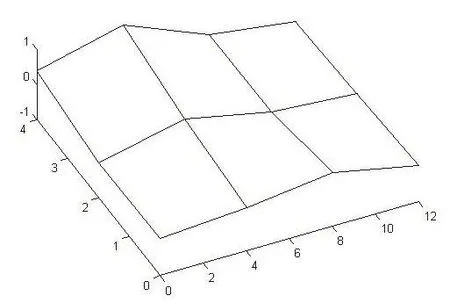
图4 第二阶振型
可以看出,基于连续小波变换的模态识别方法很好的解耦了车门的模态参数。
4 结论与展望
通过以上理论分析和实验验证,可以利用小波变换,可以对高速列车车门进行模态参数识别。但该方法在强噪声背景下的识别效率需要进一步的研究。此外,现阶段的模态识别,均假设结构的振动特性是线性的,而且假设外部激励是平稳的。所以,这种方法在结构非线性和外部激励多样化的模态解耦效果仍有待考虑研究与改进。
[1] 雷明准,张丰利,王建楠,陈剑.基于有限元的车门模态分析与优化研究[J].设计计算研究,2008(12):4-7.
[2] 朱宏平.结构损伤检测的智能方法[M].北京:人民交通出版社,2009:28-30.
[3] 李宏男.结构健康检测[M].大连:大连理工大学出版社,2005:246-260.
[4] 伊廷华,李宏男,王国新.基于小波变换的结构模态参数识别[J].振动工程学报,2003,19(1):51-56.
[5] Robert X Gao,Ruqiang Yan.Wavelets theory for manufacturing[M].New York:Springer,2011:205-207.
[6] 刘宁.系统模态参数辨识的连续小波方法研究[D].天津:天津大学,2000.
[7] 罗光坤,张令弥.基于Morlet小波变换的模态参数识别研究[J].振动与冲击,2007,26(7):135-138.
[8] 朱宏平,翁顺.运用小波分析方法进行结构模态参数识别[J].振动与冲击,2007, 26(4):1-4.

