一种砂砾岩介质岩心表征的新方法

姚 军，王晨晨，杨永飞，王 鑫，汲广胜，高 莹

（中国石油大学（华东）石油工程学院，山东 青岛 266580）

1 引 言

砂砾岩介质受到岩性、沉积环境和成岩作用的影响，碎屑颗粒尺寸变化大、分选性差，渗透率在纵向上，存在严重非均质性。砂砾岩储层的强非均质性以及砂砾岩油藏渗流和开发特征的复杂性，使得描述水驱油流动机制更加困难[1－2]，如何正确表征砂砾岩岩心结构特征对认识砂砾岩储层的渗流机制和合理开发砂砾岩油田有着十分重要的意义[3]。近些年来，随着计算机硬件技术的发展和图形学领域的重大进展，基于图像分析的微观模拟技术得到迅速发展，本文根据砂砾岩岩心的扫描电镜图像，选取不同的层位分别构建相应的数字岩心，通过合并法，构建能够描述整个砂砾岩岩心特征的数字岩心，以此为平台分析砂砾岩岩心的特征。

2 岩心表征方法

2.1 图像分析

针对典型砂砾岩油藏真实岩心，通过扫描电子显微镜(SEM)得到其灰度图像，利用最大类间距法对灰度图像进行分割可得到相应的二值图像（见图1）[4]。该样品薄片的分辨率为 2微米/像素，像素数目2000×1750个，物理尺寸4 mm×3.5 mm。由图1可以看出，该砂砾岩岩心非均质性强，具有明显的层间非均质性，根据颗粒大小从上至下呈现粗、细、粗的3层分布特征。

图1 砂砾岩油藏岩心薄片Fig.1 Core slice sandy-conglomerate

为了精确描述各层颗粒和孔隙的分布特征，将砂砾岩二值图像进行分割，从上至下分为3层，见图2。图中，第一层图像像素数目1000×600个，物理尺寸 2 mm×1.2 mm；第二层图像像素数目650×450个，物理尺寸1.3 mm×0.9 mm；第三层图像像素数目1000×600个，物理尺寸2 mm×1.2 mm。以像素为基础，对该图像进行分析，可得到各层二值图像的孔隙度依次为0.27、0.21、0.33，这些信息构成了下一步重构三维数字岩心的基础。

图2 选取不同层位代表性的岩心图像Fig.2 Representative rock core slices of different layers

2.2 数字岩心的构建

马尔可夫链蒙特卡洛法是一种特殊的蒙特卡洛方法，它将随机过程中的马尔可夫链应用到蒙特卡洛模拟中，以实现动态模拟，能够大大提升了构建数字岩心的速度[5]。采用马尔可夫链蒙特卡洛法构建三维数字岩心的具体步骤如下：①模拟一维链开始的体素，采用薄片的孔隙度作为第一个体素状态为孔隙的条件概率；②沿y方向模拟第一层第一行上的体素；③沿x方向模拟第一层各行体素进而构建该层所有体素；④沿z方向模拟各层体素进而构建三维模型。

分别基于砂砾岩岩心不同层位的二值图像，通过马尔可夫链蒙特卡洛法可构建出相应的三维数字岩心，见图 3。各数字岩心孔隙度和对应的二值图像基本一致，数字岩心体素数目均为300×300×100个，物理尺寸为 600 μm×600 μm×200 μm。

图3 三维数字岩心的构建Fig.3 Construction of 3D digital rock core

2.3 合并法

原始砂砾岩岩心从上至下分为粗、细、粗3层，为了描述整个砂砾岩岩心的层间特征，需要单独各层的数字岩心进行合并。三维数字岩心的数据体是用二进制0和1来进行表示的，其中，0表示岩石孔隙；1表示岩石骨架，因此可按照各层顺序直接将数据体文件进行拼接，从而实现各层数字岩心的合并。

由于以数字岩心为平台的渗流模拟计算成本很高，需要对数字岩心进行简化处理，即要提取由简单形状的孔隙喉道组成的，能够反映实际岩样特征的孔隙网络模型作为研究平台[6－7]。孔隙网路模型提取的具体步骤如下：数字岩心优化处理；孔隙空间居中轴线的构建及优化；最后建立起具有真心岩心孔隙空间拓扑结构和几何特征的孔隙网络模型。

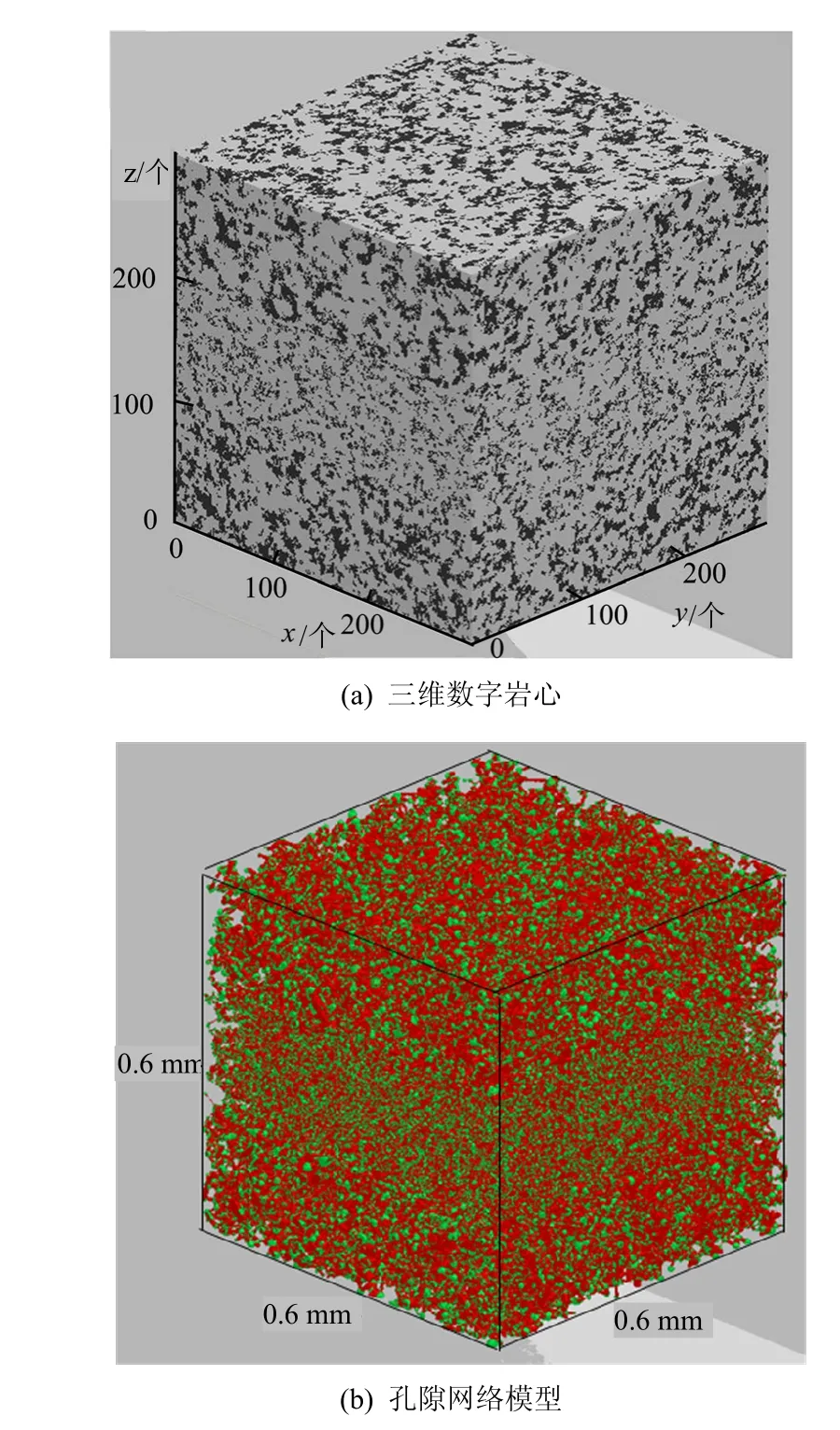
图4 合并法构建的三维数字岩心和孔隙网络模型Fig.4 3D digital rock and the corresponding pore network model with mergence method

通过合并法可构建描述各层非均质性特征的三维数字岩心，并提取相应的孔隙网络模型，见图4。图中，数字岩心孔隙度为 0.265，体素数目为300×300×300个，分辨率为2微米/像素。为便于对比研究，这里同时使用了常规法来构建三维砂砾岩数字岩心，即直接基于整个砂砾岩岩心的二值图像（见图 1）来构建三维数字岩心，并提取相应的孔隙网络模型，见图 5。其中，数字岩心孔隙度为0.2489，体素数目为300×300×300个，分辨率为2微米/像素。

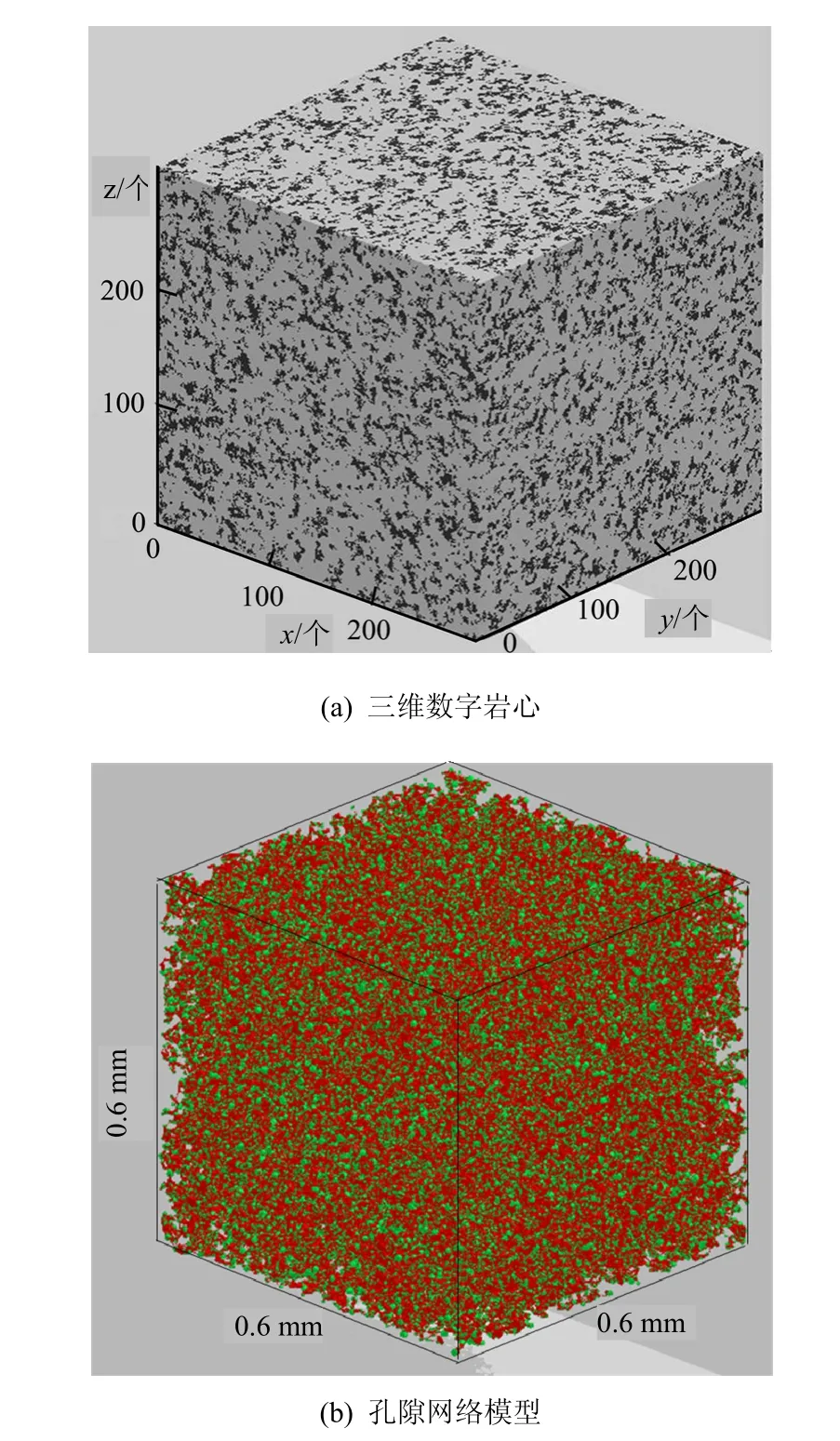
图5 常规法构建的三维数字岩心和孔隙网络模型Fig.5 3D digital rock core and pore network model with conventional method

3 岩心性质分析

基于孔隙网络模型，可对比分析不同方法表征岩心的结构特征，并模拟流体的渗流过程，进而分析其渗透率特征。

3.1 岩心结构

孔隙网络模型由孔隙及与之相连的孔喉组成。极其不规则的孔隙和喉道空间通过为截面形状为规则的圆形、三角形和矩形来进行表征。通过统计孔隙网络模型孔隙和喉道信息可得到岩心的基本结构参数见表 1。由表可以看出，通过合并法和常规法得到的孔隙网络模型平均配位数和孔隙度基本一致，孔隙和喉道数目巨大，这是由于大量碎屑颗粒造分布成的，符合典型的砂砾岩油藏特征。

表1 岩心基本结构参数Table1 Basic rock core structure parameters

3.2 绝对渗透率

将孔隙网络模型考虑为一种拟稳态模型，即流动完全由毛细管力控制，模型中由黏滞力所造成的压降同毛管压力相比可以忽略。根据侵入-逾渗理论，流体从一个孔隙流动到另一个孔隙是瞬时的，不考虑孔喉中的流动过程。流体为不可压缩牛顿流体。模型的绝对渗透率可以通过整个模型只饱和一种流体，给模型施加一个驱动压力，利用达西公式来进行计算[8]。

选择不同的封闭边界条件，分别模拟流体从水平方向和垂直方向在孔隙网络模型中的单相流动过程，可以得到模型在不同方向的渗透率。通过合并法，得到孔隙网络模型的横向渗透率为177.5 mD，纵向渗透率为33.95 mD；通过常规法，得到的孔隙网络模型的横向渗透率为62.58 mD，纵向渗透率为55.73 mD，发现常规法得到的孔隙网络模型在横向和纵向渗流率相差不大，不能有效描述砂砾岩的各向异性特征。但从通过合并法得到的孔隙网络模型能够明显看出，该砂砾岩岩心的横向渗透率远大于纵向渗透率，能够较好地模拟砂砾岩油藏的层间非均质性和各向异性特征。

4 结 论

（1）马尔可夫链蒙特卡洛法能够基于真实岩心样品薄片，大大提升了三维数字岩心的重构速度，进而分析岩心的结构特征和流动特征。

（2）合并法和常规法均能够得到砂砾岩油藏的孔隙网络模型，其平均配位数和孔隙度基本一致，孔隙和喉道数目巨大，这是由于大量碎屑颗粒分布造成的，符合典型的砂砾岩油藏特征。

（3）常规法和合并法得到的孔隙网络模型在描述岩心各向异性特征上差别较大。常规法得到的孔隙网络模型在横向和纵向渗流率相差不大，不能有效描述砂砾岩的各向异性特征；而通过合并法得到的孔隙网络模型能够明显看出，该砂砾岩岩心的横向渗透率远大于纵向渗透率，能够较好的模拟砂砾岩油藏的层间非均质性和各向异性特征，这为砂砾岩油藏岩心的精确表征及渗流机制的分析提供了一套有效地研究思路。

[1]昝灵,王颅华,张枝焕,等. 砂砾岩储层研究现状[J].长江大学学报(自然科学版),2011,8(3): 63－66.ZAN Ling,WANG Shun-hua,ZHANG Zhi-huan，et al.Research status of sandy conglomerates reservoir[J].Journal of Yangtze University (Nat Sci Edit),2011,8(3): 63－66.

[2]张丽艳. 砂砾岩储层孔隙度和渗透率预测方法[J]. 测井技术,2005,29(3): 212－215.ZHANG Li-yan. Porosity and permeability predictions in sand-conglomerate reservoir from conventional well logs[J]. Well Logging Technology,2005,29(3): 212－215.

[3]赵秀才,姚军,衣艳静,等. 基于择多算子的随机搜索法建立数字岩心的新技术[J]. 岩土力学,2008,29(5):1339－1344.ZHAO Xiu-cai,YAO Jun,YI Yan-jing et al. A new method of constructing digital core utilizing stochastic search algorithm based on majority operator[J]. Rock and Soil Mechanics,2008,29(5): 1339－1344.

[4]赵秀才. 数字岩心及孔隙网络模型重构方法研究[D].东营: 中国石油大学(华东),2009.

[5]WU K J,VAN DIJKE M I J,COUPLES G D,et al. 3D stochastic modelling of heterogeneous porous media－Applications to reservoir rocks[J]. Transport in Porous Media,2006,65(3): 443－467.

[6]陶军,姚军,李爱芬,等. 利用孔隙级网络模型研究油水两相流[J]. 油气地质与采收率,2007,14(2): 74－77.TAO Jun,YAO Jun,LI Ai-fen,et al. Research on oil and water flow using pore-scale network model[J]. Petroleum Geology and Recovery Efficiency,2007,14(2): 74－77.

[7]姚军,陶军,李爱芬. 利用三维随机网络模型研究油水两相流动[J]. 石油学报,2007,28(2): 94－97.YAO Jun,TAO Jun,LI Ai-fen. Research on oil-water two-phase flow using 3D random network model[J]. Acta Petrolei Sinica,2007,28(2): 94－97.

[8]姚军,赵秀才. 数字岩心及孔隙级渗流模拟理论[M].北京: 石油工业出版社,2010.