独立指数分布卷积的矩的计算

丁 勇

（南京医科大学数学教研室，南京 210029）

独立指数分布卷积的矩的计算

丁 勇

（南京医科大学数学教研室，南京 210029）

求和；指数分布；矩

1 引 言

矩是随机变量的重要数字特征.对于随机变量X，若E（Xr）存在，则称它为X的r阶原点矩；若E（［X－E（X）］r）存在，则称它为X的r阶中心矩.一阶原点矩即为数学期望，二阶中心矩即为方差，而偏度与峰度则与三阶、四阶矩有关［1］，利用各阶矩可对随机变量分布的参数进行估计.近年来，高阶矩在其它领域的应用日益广泛［2－6］.高阶矩计算量大，找到简便计算公式或易于计算机计算的算法，很有必要［7－9］.

指数分布是最常用的分布之一，在Poisson过程、增殖过程、更新过程和生存分析等方面有重要应用［10］.本文探讨独立指数分布卷积的矩的计算问题.为此先解决如下求和公式

其中λi为s个互不相同的实数，s，r为整数，且s≥2，简记为θs，r.

对0≤r＜s，θs，r的求和结果已得到［10－11］

下面讨论θs，r其它各种情况的计算公式.

2 r≥s的递推公式

故（4）式成立.

上述递推公式特别适用于计算机编程.

3 r＜0的转换公式

4 特殊情况的解析公式

证取r＝－1，由（5），（2）式可得（9）式.取r＝－2，由（5），（6）式可得（10）式.取r＝－3，由（5），（7）式可得（11）式.取r＝－4，由（5），（8）式可得（12）式.

5 λi有相等的极限公式

在（1）式的θs，r定义中，要求λi互不相同，但从（6）～（8）式看出，λi可以相同，甚至全都相同，这提示我们有如下的极限公式.

6 独立指数分布卷积的矩的计算

设X1，X2，…，Xs是s个相互独立的服从指数分布的随机变量，Xi的密度函数为

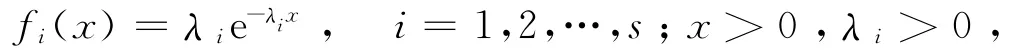
则它们的和X＝X1＋X2＋…＋Xs的密度函数为各Xi的密度函数的卷积［9－10］

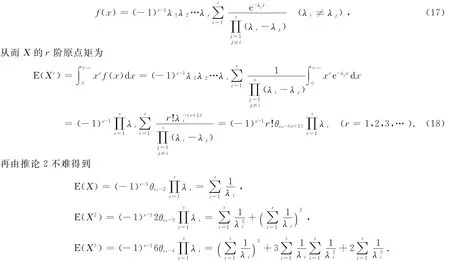
更高阶的原点矩的计算量更大，公式复杂，寻找简便计算方法很有必要，命题2和命题1较好地解决了这一问题.

在（17），（18）式中假定了λi≠λj，由命题3可知，实际上可取消λi≠λj的限制，从而对于λi＝λj也可计算各阶矩.

证X的密度函数为Xi的密度函数的n次卷积，服从gamma分布［10］.由（18），（5），（15）可得E（Xr）的表达式.

［1］王学民.应用概率统计［M］.上海：上海财经大学出版社，2005.

［2］丁勇.静注Michaelis－Menten消除动力学模型的统计及其近似计算矩［J］.生物数学学报.1995，10（4）：180－184.

［3］Brown，Geoffrey W.Higher order moments of renewal counting processes and Eulerian polynomials［J］.Statistics＆Probability Letters，2008，78（17）：3008－3013.

［4］Singh Sarjinder，Chen Cheng C.Utilization of higher order moments of scrambling variables in randomized response sampling［J］.Statist Plann Inference，2009，139（9）：3377－3380.

［5］Nayak，Tapan K.Study of the Fluctuations of Net－charge and Net－protons Using Higher Order Moments［J］.Nuclear Physics A，2009，830（4）：555－558.

［6］Dong Yinfeng，Zhang Jianying，Yan Guangwu.A higher－order moment method of the lattice Boltzmann model for the conservation law equation［J］.Applied Mathematical Modelling，2010，34（2）：481－494.

［7］李金秋.二项分布高阶原点矩的一种简便算法［J］.辽宁石油化工大学学报，2008，28（1）：89－91.

［8］朱振广，张志文.求解Poisson分布和二项分布高阶矩的代数方法［J］.辽宁工学院学报，2005，25（1）：68—70.

［9］Kitamura，Y.Calculation of higher moments of the neutron multiplication process in a time－varying medium［J］.ANNALS OF NUCLEAR ENERGY，2007，34（5）：385－395.

［10］蒋庆琅.随机过程原理与生命科学模型［M］.方积乾译.上海：上海翻译出版公司：1987：128－131，57，52.

［11］丁勇.一类指数和函数的性质和应用［J］.数学的实践与认识，2005，35（11）：194－198.

Moment Calculation for Convolution of the Independent Exponential Distribution

DINGYong
（Department of Mathematics，Nanjing Medical University，Nanjing 210029，China）

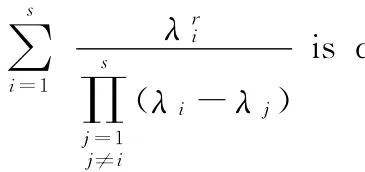
exponential distribution；convolution；moment

O211

C

1672－1454（2012）04－0124－05

2010－03－25；［修改日期］2010－07－09