滑坡降雨阈值模型的应用
何玉琼,徐则民,王志奇,张 勇
1.昆明理工大学交通工程学院,昆明 650500 2.昆明理工大学建筑工程学院,昆明 650500 3.云南省公路科学技术研究所,昆明 650051
滑坡降雨阈值模型的应用
何玉琼1,徐则民2,王志奇3,张 勇3
1.昆明理工大学交通工程学院,昆明 650500 2.昆明理工大学建筑工程学院,昆明 650500 3.云南省公路科学技术研究所,昆明 650051
在数字高程模型(DEM)的基础上,运用滑坡降雨阈值模型,以楚雄丁家坟一斜坡作为试验研究工点,结合现场勘察、监测数据以及斜坡岩土体主要特性、地形地貌、降雨强度与降雨持续时间、地下水位等因素,模拟斜坡单元产生潜在滑动时的临界降雨量,研究降雨对滑坡发生、分布的影响。研究结果表明:各斜坡单元产生潜在滑动时的临界降雨量各不相同,在不同的降雨量及地下水位条件下滑坡降雨阈值模型模拟的潜在滑坡位置主要位于楚勐公路下边坡处,与实际发生滑坡的位置吻合率达80%以上,滑坡降雨阈值模型可实现对斜坡稳定性进行可视化分析与预测,为降雨型滑坡提供一种有效的预测与分析方法。
降雨阈值;滑坡;斜坡稳定
滑坡在山区广泛分布,存在一定的危险性,会导致巨大的经济损失和环境问题。产生滑坡的因素可以分为两类[1]:一是静态因素,如地质、岩土工程性质、坡度、坡向等;二是动态因素,如水文过程、人类活动等。很多滑坡特别是浅层滑坡,降雨是主要的诱发因素。因此,运用降雨数据对滑坡进行预测,研究滑坡预报模型成为一个重要的研究课题。有学者[2-6]运用统计模型考虑地形、岩性、地质构造、地表覆盖、前期降雨量、日降雨量等因素,对斜坡进行分析,该方法可用于大面积的浅层滑坡敏感性评估,但其结果易受到使用分析数据的影响。另外一些学者[7-9]分析降雨强度与持续时间对滑坡产生的影响,他们得到临界降雨量阈值曲线,但因缺少物理过程分析,这些方法不能评价特定斜坡在一定降雨特征情况下的稳定性,也不能预测激发滑坡的降雨量。还有一些学者[10-13]运用空间分布与物理基础模型结合水文模型来分析斜坡稳定性问题,这种模型能提供一个可视化的浅层滑坡激发过程。文献[10]斜坡稳定性分析方法中没有考虑土壤水的暂态流,仅考虑土的密度、内摩擦角,这种简化将影响模型预测浅层滑坡的能力。文献[14]认为斜坡失稳的主要激发机制是由于土层与基岩接触面之间或者是降雨过程中产生的不连续湿润锋面上产生的土壤孔隙水压力的作用。笔者耦合斜坡稳定与水文学模型,在DEM的基础上考虑斜坡岩土体的主要特性、地形地貌等,研究降雨持续时间与降雨强度激发浅层滑坡的降雨阈值模型,对浅层滑坡的产生进行可视化的预测与分析。
1 工点概况
研究工点位于双柏县楚(雄)勐(醒)公路K64+200处,丁家坟村的西南侧。东经101°02′,北纬24°13′。自然地形坡度在15°~25°,局部斜坡较陡。钻探资料表明:1)0~1.2 m人工填土,褐灰、褐黄、紫红色,成分为碎石、碎砖及黏性土;2)1.1~11.50 m残坡积物,褐红、紫红色含角砾粉质黏土、角砾土;3)11~30 m侏罗系上统妥甸组上段紫红、灰色泥岩夹粉砂岩,其中滑坡中上部以紫红色为主,下部为灰、紫红色,按物理力学性质及风化程度分为全风化泥岩夹粉砂岩、强风化泥岩夹粉砂岩、中风化泥岩夹粉砂岩。地下水主要赋存于第四系残坡积含角砾粉质黏土层、角砾土层及基岩裂隙中,地下水类型为孔隙潜水、裂隙水,局部微具承压性,主要接受大气降水补给。勘察期间地下水稳定在1 747.23~1 816.37 m,地下水总体由南西向北东径流,局部地段受地形影响,其流向与地形坡向基本一致。工点地处亚热带高原季风气候区,干湿季节分明,年平均气温15℃,年降雨量700~800 mm。工作区附近除丁家河外,无其他较大地表水体,丁家河位于滑坡体前缘,对边坡稳定性影响甚微。
2 滑坡降雨阈值模型
2.1 临界地下水位
假设潜在滑动面、潜水面平行于坡面[15],潜在滑动面位于地表以下的深度为Z,且这一深度远小于斜坡的长度,斜坡的边界效应可忽略不计(图1)。
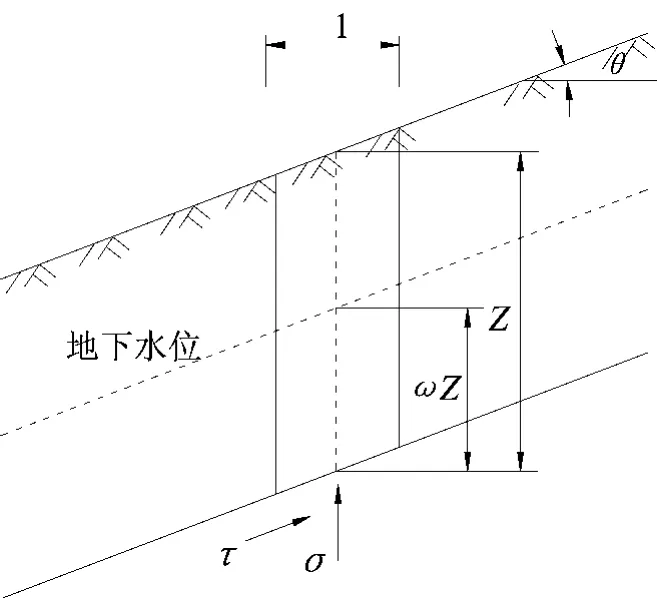
图1 斜坡平衡状态一维模型Fig.1 Slope equilibrium state one-dimensional model
地表坡度设为θ,潜水面位于潜在滑动面以上h=ωZ,0≤ω≤1(ω为地下水位系数),假设稳定渗流方向平行于坡面,滑动面上任意点的应力相同,运用Skempton等[16]1957年提出的斜坡稳定模型计算单位宽度与厚度楔体的稳定系数为

式中:τf为滑动面上土的抗剪强度;τ为剪应力。
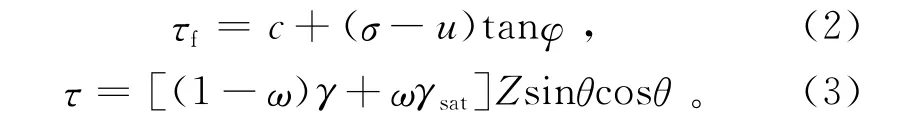
式(2)中:c为土的黏聚力;σ为总正应力;u为孔隙水压力;φ为内摩擦角。式(3)中:γ为地下水位以上土的容重;γsat为土的饱和容重,其余同上。
式(2)中的总正应力σ、孔隙水压力u分别为
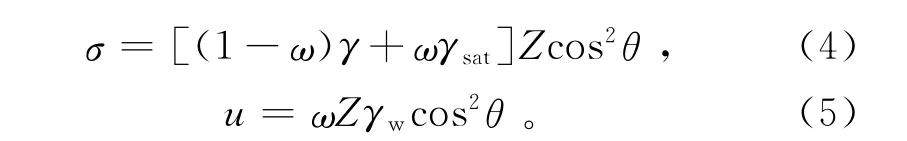
式(5)中:γw为水的容重;其余同上。
将式(2)-(5)代入(1)式中,则有
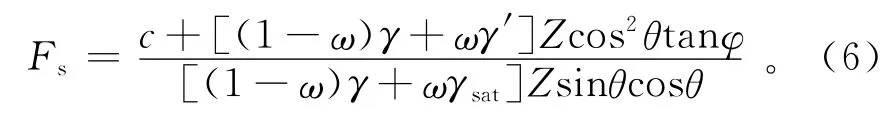
式(6)中:γ′=γsat-γw,为水下土体容重。
若在滑动面上黏聚力很小,可忽略不计,令c=0,则(6)式变为
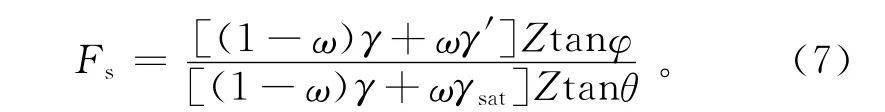
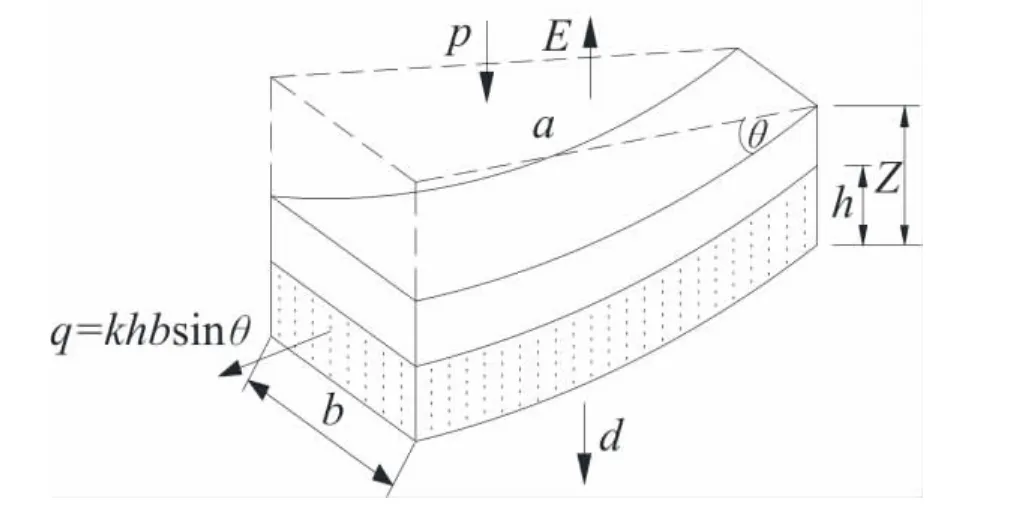
图2 单位排水面积示意图Fig.2 Unit drainage area schemes
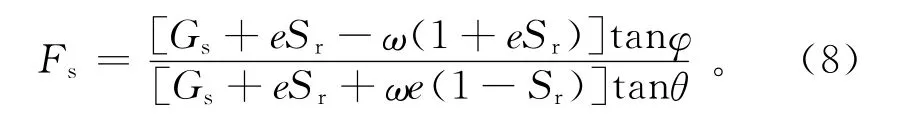
式(8)中:e为孔隙比;Sr为饱和度;Gs为土粒比重。
式(8)中:若ω=0,地下水位刚好位于滑动面上;若ω=1,则位于坡面上;若0<ω<1,介于潜在滑动面与坡面之间。斜坡处于极限平衡状态(即Fs=1)时的地下水位系数ω处于临界状态,设为ωCR,若ω<ωCR则不会产生滑坡。由式(8)可得
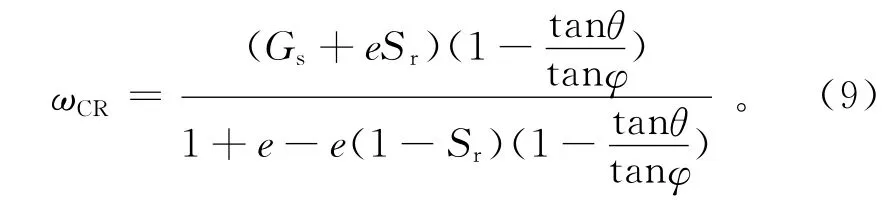
若tanθ/tanφ≤(Gs-1)/(Gs+e),斜坡无条件稳定;若tanθ/tanφ≥1,斜坡无条件不稳定;若(Gs-1)/(Gs+e)<tanθ/tanφ<1和ω<ωCR,斜坡稳定;若(Gs-1)/(Gs+e)<tanθ/tanφ<1和ω>ωCR,则斜坡不稳定。以上斜坡稳定条件已由Montgomery等[10]所证明,但其忽略了地下水位以上部分的孔隙比和土的饱和度的影响。
2.2 水文分布模型
根据斜坡地形、等高线划分分水岭,坡面水流方向与等高线垂直。假设地下水位以上土的饱和度和孔隙比为常数,则在此流通区域内某单元水的流入量与流出量如图2所示[1],可表示为
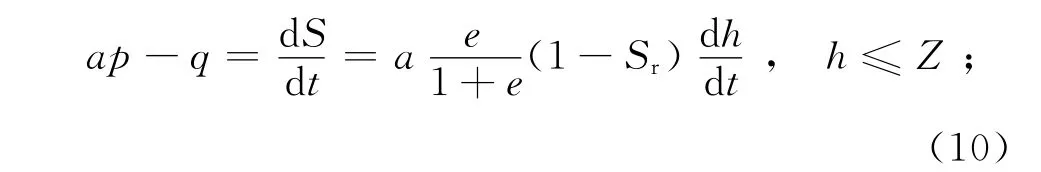
或
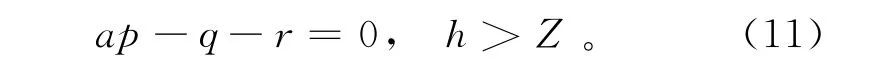
式中:a为上坡单元汇水面积[17](m2);p 为降雨量(有效降雨量+植被截留量+蒸发量+基岩入渗量)(mm/d);q为地下渗流量;r为地表径流量(当土体饱和时即Sr=1时产生地表径流);S为单元内水存贮量;t为降雨持续时间(d),其余同上。
假定水力坡降与斜坡坡降基本相等,由达西定律,宽度为b的单元地下渗流量为
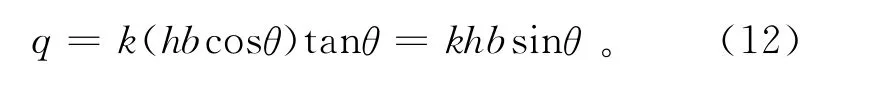
图2中E为蒸发量;d为深层渗流量;k为渗透系数,其余同上。
当斜坡土体处于饱和状态时,流经单元的径流量等于导水系数T与水力梯度sinθ及单元等高线长b的乘积。假定水力传导性在滑坡体的深度方向上均匀分布,即不随深度而产生显著的变化,则滑坡土体的导水系数T=k Z(m2/d)。
本文主要讨论非饱和斜坡土体(不产生地表径流的情况),降雨时所有降雨量全部入渗。将式(12)代入式(10)中并积分,假设地下初始水位为hi,经降雨时段t后,当时,潜水面位于潜在滑动面以上高度为
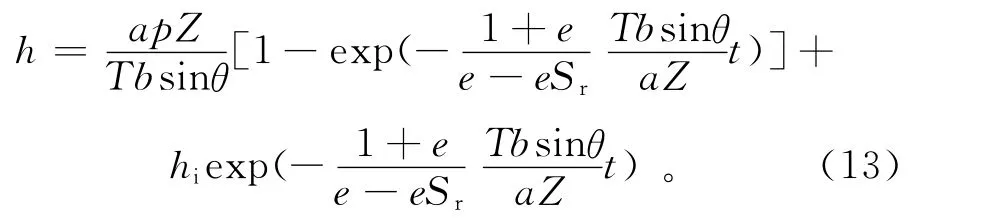
2.3 降雨阈值模型
由h=ωZ这一关系式,将式(13)等式两边同时除以Z 后,与式(9)相等,即
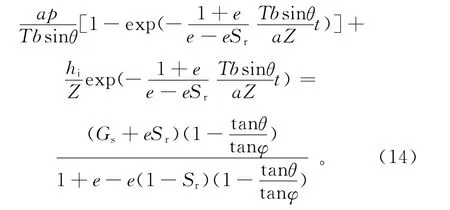
由式(14)可推导出考虑降雨持续作用(不间断降雨)下斜坡产生潜在滑动时的降雨阈值模型为
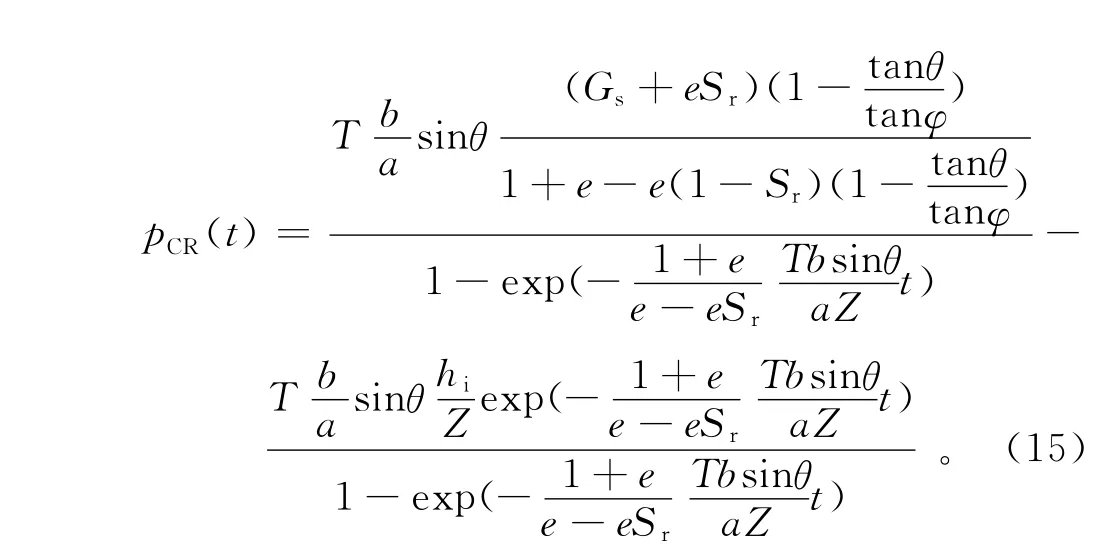
式中:pCR(t)为降雨持续时间下斜坡单元产生潜在滑动时的降雨阈值(m/d);hi为初始地下水位高度(m),其余同上。
由式(15)可知,斜坡在一定降雨条件下产生滑动,不仅与斜坡体的地质、地形、降雨量大小、降雨入渗等因素有关,还与降雨历时有关;同一雨强,其降雨持续时间不同对斜坡稳定产生的作用也不同。
3 降雨阈值的计算与稳定性分析
3.1 计算参数
根据工点钻探及土工试验资料,土的内摩擦角φ=28.7°;孔隙比e=0.46,饱和度Sr=89.3%,土粒比重Gs=2.65;渗透系数k取1×10-4m/s=8.64(m/d),滑坡土层竖直厚度Z=7 m;导水系数T=k Z=60.48 m2/d;地表坡度θ、单元等高线长b及上坡单元汇水面积a由DEM提取。
3.2 降雨阈值计算
考虑工点斜坡岩土体的内摩擦角、孔隙比、饱和度、地形、导水系数等相关因素,运用式(15)计算不同降雨持续时间下各斜坡单元产生潜在滑动时的降雨阈值(或临界降雨量)。为分析地下水位与降雨持续时间对斜坡单元稳定性的影响,地下水位初值hi分别取0、0.5、1 m;降雨持续时间分别取2、6、12、24、48、72、96、120、144 h。以此分析各斜坡单元产生潜在滑动时分别需要的临界降雨量。
将斜坡划分为2 m×2 m的DEM单元,运用ArcGIS软件计算出不同初始地下水位、降雨持续时间下各斜坡单元产生潜在滑动时所需的临界降雨量。由于各斜坡单元产生潜在滑动时所需的临界降雨量不尽相同,为了便于表述,将临界降雨量划分为以下范围:0~25、>25~50、>50~100、>100~200、>200 mm/d。由于篇幅所限,仅列出降雨持续时间为2 h、初始地下水位为0、0.5、1 m时各斜坡单元产生潜在滑动时所需的临界降雨量(图3)。
该工点斜坡在不同地下水位、降雨持续时间作用下,斜坡单元在划分的降雨量范围内潜在滑坡单元所占比例如图4所示。
经计算可知:1)随地下水位的升高,在相同降雨条件下,不稳定单元呈增加趋势;2)随降雨持续时间的增加,相同降雨条件下不稳定单元呈增加趋势,但降雨持续时间在72 h以上时,潜在滑坡单元比例相对稳定,无明显变化;3)不同初始地下水位及降雨持续时间作用下斜坡的稳定状态不相同,得到的潜在滑坡时的临界降雨量也各不相同;4)当降雨量在25~100 mm/d范围内时,位于楚勐公路路基下方的潜在滑坡单元已连成片,见图3,该位置有可能产生整体滑动;5)降雨量大于50 mm/d时潜在滑坡单元所占比例在60%以上,并有连成片的趋势;6)5.2%的斜坡单元为无条件稳定,这一部分斜坡单元所在坡度比较平缓;12.8%的斜坡单元为无条件不稳定,此部分单元受地形坡度较陡的影响;7)经计算,采用2 m×2 m的DEM栅格单元预测结果较为理想,若单元划分过小对于整体滑坡的可比性差,若划分过大则有的局部滑动位置不能统计到潜在滑坡单元中。
3.3 实际观测数据
研究工点斜坡如图5所示,该工点的降雨量、地下水位、地表位移、地下位移的监测数据分别如下:
降雨量 取2010年6月、7月两个月的监测降雨数据对斜坡进行计算分析,这一期间的降雨量如图6所示。
地下水位 各监测钻孔地表现高程ZK2>ZK7>ZK10>ZK11>ZK12。2010年6、7月各钻孔相对于渗压计布设位置的地下水位变化见图7。地下水位位于渗压计的下方为负,上方为正值。各钻孔的地下水位随降雨有上升的趋势,水位上升时间滞后于降雨时间。
位移 在降雨条件下产生一定的地表及地下位移,地表变形监测数据用全站仪监测,地下位移用测斜仪进行监测,2010年6、7月监测到的地表位移、地下位移见图8,位移产生时间滞后于降雨时间。
3.4 实测与计算结果对比分析
由实际监测值即图6-8可以看出,在2010年6、7月的降雨对研究工点的地表及地下产生一定的位移量。地下水位变化、地表及地下产生的位移量均滞后于降雨时间,从而导致斜坡在降雨作用下现场产生滑坡的时间亦滞后于降雨时间。

图3 斜坡单元潜在滑动时的降雨阈值图Fig.3 Slope unit potential sliding rainfall threshold graphs
该斜坡实际滑动位置位于楚勐公路K64+200处至左侧28 m,周界明显,呈圈椅状,如图5,处于滑动破坏状态。剪出口大致位于第一段较陡边坡坡脚处,滑坡主滑方向为84°,沿主滑方向平均长35 m,平均宽度40 m,平均深度7.5m。该滑坡变形明显,边坡上剪出变形明显,局部已滑动;后缘破裂缝宽0.1~0.4 m,后壁高0.5~1.5 m。滑体内拉张裂缝和滑坡后缘破裂缝及两侧剪切张裂缝发育,滑坡周界裂缝已贯通。
降雨入渗使滑体及滑带土的含水量增加,而含水量的增加使土体容重增加,同时使土体的抗剪强度明显降低,抗剪强度的降低幅度与土体性质和饱水作用时间有关,对易泥化或饱水作用时间较长的边坡,其抗剪强度降低甚为严重,对斜坡稳定及变形极为不利[18]。由于滑坡的破坏是一个长期变形积累过程,滑坡体上通常发育较多的拉张裂隙,当降雨强度较大时,地表积水将沿裂隙快速渗入到地下,对暴雨型滑坡的发生有很大影响;当有裂隙存在时,斜坡体内的渗流场才会有较快速的变化,斜坡的稳定性才有比较显著的降低[19]。
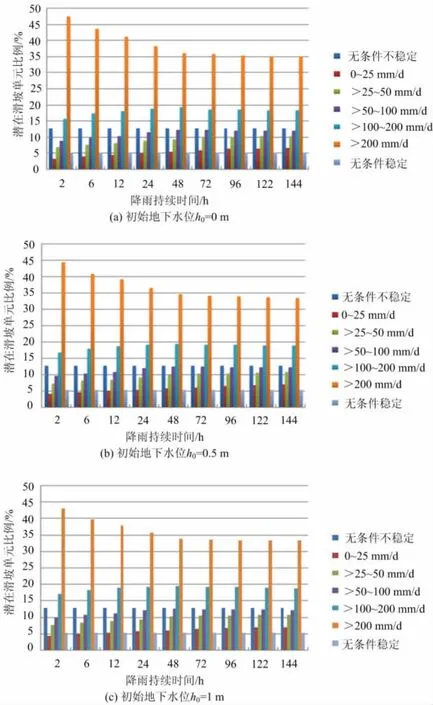
图4 潜在滑动斜坡单元所占比例Fig.4 The proportion of potential sliding slope unit
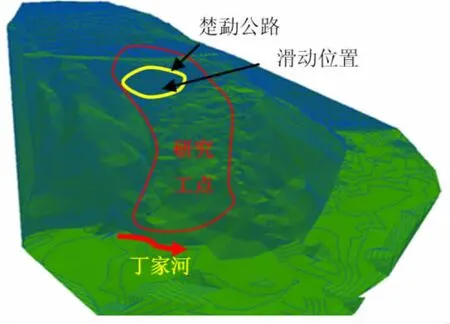
图5 研究工点斜坡图Fig.5 Research worksite slope figure
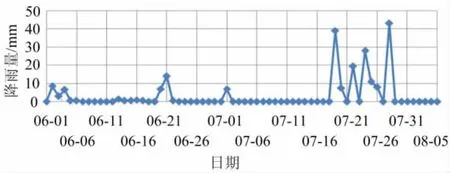
图6 降雨量曲线图Fig.6 Rainfall graph
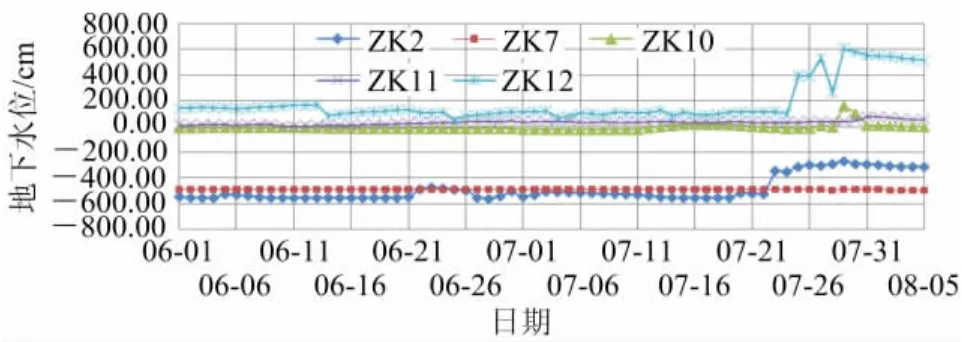
图7 地下水位变化图Fig.7 The underground water level variations
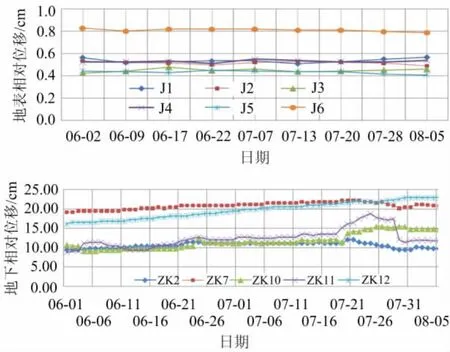
图8 位移Fig.8 Displacement
该滑坡的形成是由于边坡较陡,工程地质条件差,滑坡体岩土层为黏结力较差的粉质黏土和易水化钙质泥岩,在降雨入渗情况下,原坡体的应力平衡状态遭破坏,从而诱发滑坡体滑动破坏形成滑坡。由于实测期间降雨量不大,最大日降雨量为43 mm/d,降雨量在50 mm/d以内,对比图3与图5可知,降雨阈值模型计算出的潜在滑坡单元主要出现在楚勐公路K64+200路基下方边坡,与现场实际发生滑坡的位置基本一致,吻合率达80%以上,说明基于DEM预测模拟斜坡潜在滑动时的降雨阈值模型研究工点滑坡位置及其临界降雨量是可行的。
4 结论
在DEM的基础上运用滑坡降雨阈值模型进行斜坡的稳定性研究,结合斜坡的地形地貌、坡度、斜坡单元汇水面积、地质等因素加以综合分析,可确定斜坡产生滑动与降雨量的定量关系,为斜坡稳定性研究提供一种有效、可视化的分析方法。通过计算可以得出以下结论:
1)运用降雨阈值模型计算斜坡单元潜在滑坡时的临界降雨量,位于楚勐公路路基下方产生潜在滑坡时的临界降雨量在25~100 mm/d范围内,并且潜在滑坡单元已连成片,该位置极有可能产生整体滑动,其位置与现场实际滑坡位置基本一致,吻合率达80%以上,说明降雨阈值模型模拟斜坡产生潜在滑动时所需临界降雨量是可行的。
2)在降雨量作用下,工点斜坡的地表及地下产生一定的位移量,地下水位变化、地表及地下产生的位移量均滞后于降雨。
3)随着地下水位的升高,在相同的降雨条件下,潜在滑坡单元呈增加趋势;随着降雨持续时间的增加,相同降雨条件下潜在滑坡单元呈增加趋势,但降雨持续时间在72 h以上时,潜在滑坡单元比例相对稳定,无明显变化。
4)各斜坡单元产生潜在滑动时的临界降雨量各不相同,降雨量大于50 mm/d时的潜在滑坡单元所占比例在60%以上(包含无条件不稳定单元),并有连成片的趋势。
(References):
[1] Rosso R,Rulli M C,Vannucchi G.A Physically Based Model for the Hydrologic Control on Shallow Landsliding[J].Water Resources Research,2006,42:1-16.
[2] Hollingsworth R,Kovacs G S.Soil Slump and Debris Flows:Prediction and Protection[J].Bull Assoc Eng Geol,1981,18:17-28.
[3] Crozier M J.Prediction of Rainfall-Triggered Landslides:A Test of the Antecedent Water Status Model[J].Earth Surf Processes Landforms,1999,24:825-833.
[4] Glade T,Crozier M,Smith P.Applying Probability Determination to Refine Landslide Triggering Rainfall Thresholds Using an Empirical“Antecedent Daily Rainfall Model”[J].Pure Appl Geophys,2000,157:1059-1079.
[5] 李媛.四川雅安市雨城区降雨诱发滑坡临界值初步研究[J].水文地质工程地质,2005(1):26-29.Li Yuan.Preliminary Study on Precipitation Threshold of Precipitation Induced Landslides in Ya’an Yucheng District,Sichuan Province[J].Hydrogeology & Engineering Geology,2005(1):26-29.
[6] 李媛,杨旭东.降雨诱发区域性滑坡预报预警方法研究[J].水文地质工程地质,2006(2):101-107.Li Yuan,Yang Xu-dong.Research on the Forecasting and Early Warning of the Regional Precipitation-Induced Landslid[J].Hydrogeology & Engineering Geology,2006(2):101-107.
[7] Caine N.The Rainfall Intensity-Duration Control of Shallow Landslides and Debris Flows[J].Geogr Ann Ser A,1980,6:23-27.
[8] Cancelli A,Nova R.Landslides in Soil Debris Cover Triggered by Rrainstorms in Valtellina(Central Alps-Italy)[C]//Proceedings 4th International Conference on Landslides.Tokyo:Geol Soc,1985:267-272.
[9] Cannon S H,Ellen S D .Rainfall Conditions for A-bundant Debris Avalanches in the San Francisco Bay Region[J].California Geol,1985,38(12):267-272.
[10] Montgomery D R,Dietrich W E.A Physically Based Model for the Topographic Control on Shallow Landsliding[J].Water Resour Res,1994,30:1153-1171.
[11] Dietrich W E,Reiss R,Hsu M L,et al.A Process Based Model for Colluvial Soil Depth and Shallow Landsliding Using Digital Elevation Data[J].Hydrol Processes,1995,9:383-400.
[12] 武利,张万昌,张东,等.基于遥感与地理信息系统的分布式斜坡稳定性定量评估模型[J].地理科学,2004,24(4):458-464.Wu Li,Zhang Wan-chang,Zhang Dong,et al.Remote Sensing & GIS Based Distributed Hillslope Sta-bility:Quantitative Evaluation Model[J].Scientia Geographica Sinica,2004,24(4):458-464.
[13] 兰恒星,伍法权,周成虎,等.GIS支持下的降雨型滑坡危险性空间分析预测[J].科学通报,2003,48(5):507-512.Lan Heng-xing,Wu Fa-quan,Zhou Cheng-hu,et al.Under the GIS Support Rainfall Type Landslide Hazard Spatial Analysis and Prediction[J].Chinese Science Bulletin,2003,48(5):507-512.
[14] Megahan W F.Hydrologic Effects of Clearcutting and Wildfire on Steep Granitic Slopes of Idaho[J].Water Resour Res,1983,19,811-819.
[15] Tarolli P,Borga M,Fontana G D.Analysing the Influence of Upslope Bedrock Outcrops on Shallow Landsliding[J].Geomorphology,2008,93:186-200.
[16] Skempton A W,DeLory F A .Stability of Natural Slopes in London Clay[J].Proc Int Conf Soil Mech Found Eng,1957,4(2):378-381.
[17] 兰恒星,周成虎,王苓涓,等.地理信息系统支持下的滑坡-水文耦合模型研究[J].岩石力学与工程学报,2003,22(8):1309-1314.Lan Heng-xing,Zhou Cheng-hu,Wang Ling-juan,et al.GIS Based Landslide Stability and Hydrological Distribution Coupled Model[J].Chinese Journal of Rock Mechanics and Engineering,2003,22(8):1309-1314.
[18] 李守升,植被护坡水运移及浅层边坡稳定性分析[D].成都:西南交通大学,2009.Li Shou-sheng.Water Movement in Bio-Slope-Engineering and Stability Analysis of the Shallow Slope[D].Chengdu:Southwest Jiaotong University,2009.
[19] 刘礼领,殷坤龙.暴雨型滑坡降水入渗机理分析[J].岩土力学,2008,29(4):1061-1066.Liu Li-ling,Yin Kun-long.Analysis of Rainfall Infiltration Mechanism of Rainstorm Landslide[J].Rock and Soil Mechanics,2008,29(4):1061-1066.
Application of Landslide Rainfall Threshold Model
He Yu-qiong1,Xu Ze-min2,Wang Zhi-qi3,Zhang Yong3
1.Faculty of Transportation Engineering,Kunming University of Science and Technology,Kunming 650500,China 2.Faculty of Architectural Engineering,Kunming University of Science and Technology,Kunming 650500,China 3.Yunnan Institute of Highway Science and Technology,Kunming 650051,China
Based on digital elevation model(DEM),the slope in Dingjiafen,Chuxiong was taken as an experimental research worksite to study the effect of rainfall on landslide occurrence and distribution by means of landslide rainfall threshold model(LRTM).The critical rainfall for a slope unit to generate a potential sliding was simulated combined with field investigation,monitoring data,main features of the slope rock and soil mass,topography and geomorphology,rainfall intensity and duration,underground water level and other factors.Results showed that the critical rainfall to cause a potential sliding varies in each slope.In different rainfall and groundwater level conditions,according to the simulation of LRTM the potential landslide position was mainly located below Chu-Meng highway,leading to a more than 80%agreement rate with the actual landslide position.Visual analysis and prediction of slope stability can be realized through LRTM,which provide an effective method for the forecast and analysis of rainfall-induced landslide.
rainfall threshold;landslides;slope stability
P642.22
A
1671-5888(2012)04-1112-07
2011-10-19
国家自然科学基金项目(40572159,40772189);NSFC-云南联合基金重点项目(U1033601);交通部西部科技项目(200831876723);云南省教育厅基金项目(09Y0076)
何玉琼(1975-),女,侗族,博士研究生,讲师,主要从事公路工程和斜坡稳定方面工作,E-mail:hyqkm@yahoo.com.cn。

