一种适用于超声多普勒血流速度测量的混沌调频连续波的研究*

彭京思 彭虎

1)(中国科学技术大学电子科学与技术系,合肥 230027)

2)(合肥工业大学生物医学工程系,合肥 230009)

1 引言

医学超声多普勒血流测量利用血流中红细胞对超声信号的散射,由超声探头探测包含多普勒频移的回波信号,以实时监测血液的流动状况.超声多普勒测量系统可分为连续波多普勒系统和脉冲波多普勒系统两大基本类型.

通常的超声连续波多普勒血流测量系统是由换能器发射频率一定的连续超声信号,遇到运动物体(红细胞)后,反射的回声信号频率发生改变,通过解调处理得到多普勒频移信号.该信号中含有运动目标的速度,但是难以鉴别测量目标的位置,不具备距离识别能力.脉冲多普勒血流测量系统发射脉冲超声信号,能够测得具有距离信息的血流速度,但是可测速度范围受到限制,同时信噪比差[1-5].

针对连续波和脉冲波多普勒血流测量系统存在的不足,Masanori Kunita等提出基于正弦调频连续波的超声多普勒血流测量系统[6],能够提供具有距离信息的高信噪比多普勒信号,同时杂波功率低,但正弦调频连续波的超声多普勒血流测量系统存在与三角调频等周期性线性调频连续波系统一样的不足,即多普勒信号频谱在距离方向存在周期性,从而导致距离模糊[7].针对存在的问题,本研究提出基于混沌调频连续波超声多普勒血流测量方法,该系统具有连续波测量系统低功率特点,且多普勒信号频谱无周期性,并具有理想的图钉型模糊函数,这就解决了周期性距离模糊问题.

2 基于正弦调频连续波的血流速度测量

正弦调频连续波信号[6,8,9]表示为

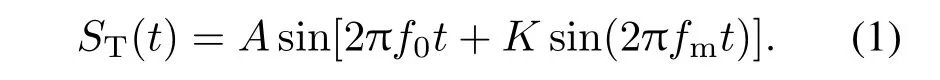
根据多普勒效应推导,假定在发射与接收端之间的传播衰减为a,fd是多普勒频率,c和v分别是超声和血流在人体组织的速度,L为测量距离,分别记实际距离为Lm,参考距离为Lr,K是调频参数,φ0和φm分别是载波和调制频率在发射与接收端的相位偏差.接收端获得信号[6]为

Jn(K)是一个n次第一类圆柱贝塞尔函数.

(7)式显示,当测量位置 Lm与 Lr的关系使 φr= φm-2nπ 时,得到的多普勒频谱没有谐波分量[6],FMCW系统中的多普勒功率与CW系统中的相等.

由于正弦或线性调频信号的周期性,难以区分延迟相位差 φr和 φr-2nπ 所对应的距离.也就是说,距离每隔ΔL=nπc/fm,所对应的sin(φr-φm)=sin(φr-2nπ-φm),这就产生了距离模糊.为了消除距离模糊,在选择调制频率时,应使一个调制周期所对应的距离范围大于可测得的距离变化范围.设L为系统能够测出的距离范围,则应使这个可测得的距离变化范围L＜c/(2fm).

3 基于混沌调频连续波的血流速度测量

由本文第二部分分析可知,正弦调频连续波血流测量在测量高速运动目标时,由于多普勒信号在距离方向上的周期性,将产生距离模糊.为解决以上问题,本文提出基于混沌调频连续波超声多普勒血流测量系统.

混沌调频连续波发射信号表示为

调制信号x(ξ)为近似零均值的混沌连续信号,A为混沌调频信号的幅度,f0为中心频率,K为调频指数.

假定在发射与接收端之间的传播衰减为a,fd是多普勒频率,c是超声在人体组织的速度,v是血流速度,L为探测血流到表面距离,τ为延迟时间,则接收到的回波信号

当参考信号延迟与回波信号延迟相等,即τr= τ时,

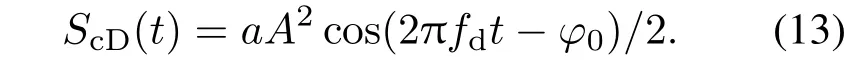
与正弦调频连续波的情况相似,得到的多普勒频谱没有谐波分量.如果参考距离与实际距离不等,得到无明显主瓣的多普勒频谱;当且仅当参考距离与实际距离一致时,得到唯一的主瓣明显的多普勒频谱,且不存在如正弦调频连续波方法的关于距离方向上周期性出现主瓣明显的多普勒频谱的情况.在实际操作中,采用回波信号与通过各个距离门延迟的参考信号相乘,通过低通滤波,再进行傅里叶变换得到多普勒频谱,根据实际距离Lm与参考距离Lr相等时,能获得理想的多普勒功率谱,该频谱主瓣明显没有其他谐波分量,多普勒功率值最大,由此确定距离与多普勒频率.

4 仿真及分析

仿真基本参数:载频f0为200 kHz,回波的多普勒频率fd为2 kHz,测量距离为10 cm,参考距离从1 cm到60 cm每隔1 cm取一次值.

4.1 基于正弦调频连续波方法仿真及分析

正弦调频连续波调制频率为5kHz,调制指数K为10.正弦调制波形如图1所示,(a)和(b)分别是调制信号和调频连续波.

仿真实验结果如图2和图3所示,图2(a)和(b)分别是当参考距离与实际距离相等时,回波信号与参考信号相乘并经过低通滤波后所得信号及多普勒功率频谱.图3(a)是对60个不同距离门延迟通道与回波信号进行卷积后的多普勒频谱图;x轴为频率,y轴为不同距离门对应的参考距离,z轴为多普勒功率,图3(b)和(c)分别是图3(a)的x-z轴和y-z轴视图,从图中可以看出,多普勒功率与距离关系具有周期性,当参考距离与实际距离相等,或距离差ΔL=nπc/fm时,多普勒功率有最大值;当图3(d)是为方便观察多普勒频谱周期性,按参考距离间隔为5 cm从图3(a)中抽取频谱作图.

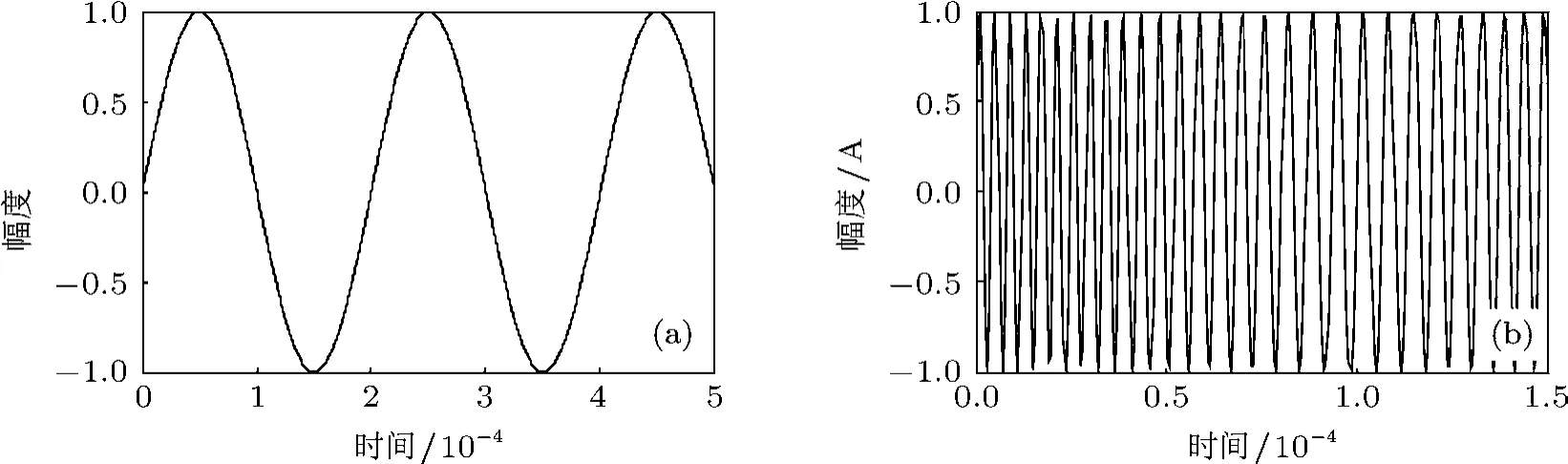
图1 正弦调频波发射信号

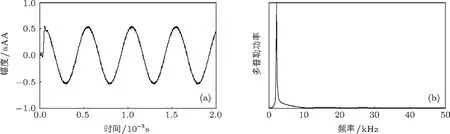
图2 基于正弦调频连续波方法的多普勒频谱

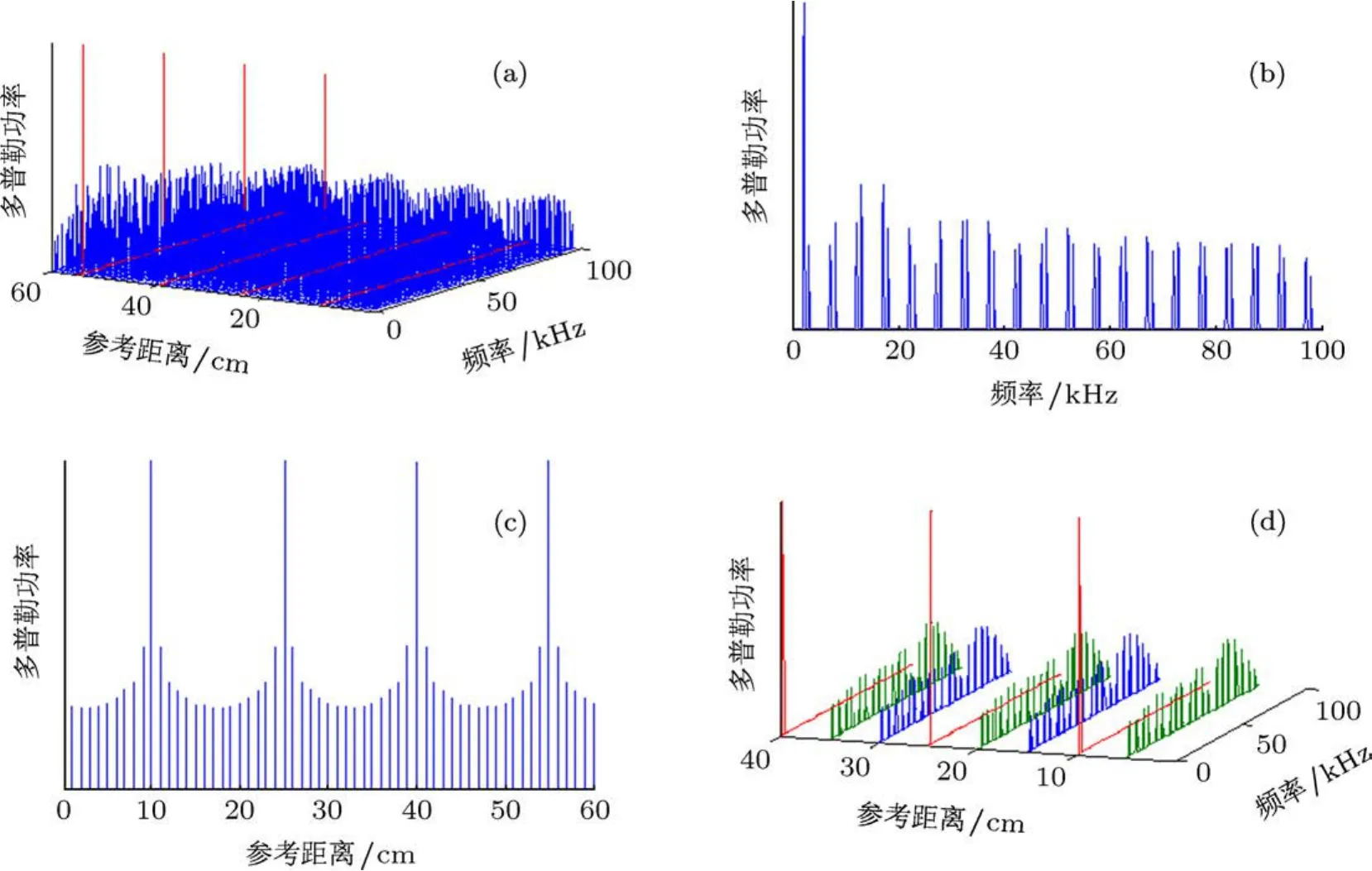
图3 不同参考距离下,基于正弦调频连续波方法的频谱特性

4.2 基于混沌调频连续波方法仿真及分析

混沌调频连续波调制信号[10,11]选取Lorenz系统信号方程(14)中x1的解进行积分:

混沌调制信号及混沌调频连续波如图5所示,(a)为积分后的调制信号,(b)为混沌调频连续波.

仿真结果如图6和图7所示,图6(a)是当参考距离与实际距离相等时,参考信号与回波信号卷积结果并经过低通滤波后图像,图6(b)是其多普勒频谱,从图中可看出主瓣明显,可检测出多普勒频移fd.图7(a)是对60个不同距离门延迟通道与回波信号进行卷积后的多普勒频谱图;x轴为频率,y轴为不同距离门对应的参考距离,z轴为多普勒功率,图7(b)和(c)分别是图7(a)的x-z轴和y-z轴视图.从图中可以看出,基于混沌调频连续波方法测量的多普勒信号频谱没有周期性,具有理想的图钉型模糊函数,解决了距离模糊.

图4 洛伦兹方程中x1的解

图5 混沌调频连续波

图6 基于混沌调频连续波方法的多普勒频谱

图7 不同参考距离下,基于混沌调频连续波方法的频谱特性

5 结论

分析和仿真结果表明,基于正弦调频连续波的方法在检测多普勒频移的同时能够根据实际距离与参考距离的匹配来确定实际距离,解决了普通连续波无法获得距离信息的不足.但因为多普勒信号频谱具有周期性,从而导致测量时存在距离模糊;本文提出基于混沌调频连续波方法,多普勒信号频谱没有周期性,能够有效测量距离和速度,解决了正弦调频连续波和脉冲多普勒血流测量系统的速度与距离限制问题.

[1]Wilhjelm J E,Pedersen P C 1993 Ferroelectrics,And Frequency Control 40 366

[2]Lasse Lovstakken,Hans Torp 2010 IEEE International Ultrasonics Symposium Proceedings USA,Oct.11-14,2010 p1198

[3]Jeremy Bercoff,Gabriel Montaldo,Thanasis Loupas,David Savery,Fabien M´EZi`ERe,Mathias Fink,Mickael Tanter 2011 IEEE Transactions On Ultrasonics,Ferroelectrics,And Frequency Control 58 134

[4]MasanoriKunita,Masamitsu Sudo,Takashi Mochizuki 2008 IEEE International Ultrasonics Symposium Proceedings USA,Nov.2-5,2008 p1366

[5]Cui Z Z,Song S H,Xu L X Theoty of Proximity Fuse.(Beijing:Beijing Institute of Technology Press)p68(in Chinese)[崔占忠,宋世和,徐立新2005近炸引信原理(北京:北京理工大学出版社)第68页]

[6]Masanori Kunita,Masamitsu Sudo,Shinya Inoue,Mutsuhiro Aka-hane 2010 IEEE Transactions On Ultrasonics,Ferroelectrics,And Frequency Control 57 p1064

[7]Lv Q,Gu H,Su W M 2010 J.Elect.Inf.Tech.32 277(in Chinese)[吕婧,顾红,苏卫民2010电子与信息学报32 377]

[8]Stove A G 1992 Radar and Signal Processing,IEE Proceedings F 139 343

[9]Liu G S,Sun G M,Gu H,Zhu X H 1995 Modern.Radar.17(6)20(in Chinese)[刘国岁,孙光民,顾红,朱晓华1995现代雷达17(6)20]

[10]Jiang F 2009 Ph.D.Dissertation(Nanjing:Nanjing University of Science and Technology)(in Chinese)[蒋飞2009博士学位论文(南京:南京理工大学)]

[11]Yu S M 2011 Chaotic Systems and Chaotic Circuits:Principle,Design and Its Application in Communications(Xi’an:Xi Dian University Press)p113(in Chinese)[禹思敏2011混沌系统与混沌电路-原理、设计及其在通信中的应用(西安:西安电子科技大学出版社)第113页]