含有用信号的自适应干扰对消系统时域分析

李文禄，赵治华，李毅，唐健，肖欢

(海军工程大学 舰船综合电力技术国防科技重点实验室，湖北 武汉 430033 )

1 引言

舰船共平台通信系统在大功率发射机和宽带接收机同时工作时，将引起辐射耦合干扰问题，影响接收机的正常接收，严重时将导致接收机阻塞。舰船共平台通信系统的辐射干扰问题，目前主要采用合理布置收发天线的位置、增大收发系统的频率间隔和采用收发系统分时工作等方式来解决。然而，由于收发天线的布置间距受舰艇空间所限，加大收发系统的频率间隔会降低频谱资源利用率，采用收发系统分时工作会极大削弱舰艇战斗力，因此传统方法不能有效解决收发系统的干扰问题。

自适应干扰对消技术是解决舰船共平台辐射干扰的一种有效方法。国外较早开始了自适应干扰对消方面的研究[1～5]，由于军事用途，公开的文献和报道较少。目前，英国ERA公司已研制出8通道干扰对消装置[6]。国内杜武林等[7]对自适应干扰对消技术进行了跟踪研究，介绍了该技术的基本原理和关键技术，并指出其在军事通信应用中的重要作用，马义广等[8]对自适应干扰对消系统的性能及影响系统性能的因素进行了分析，郑伟强等[9]对自适应干扰对消技术进行了研究，提出了一种性能优异的步进衰减器，姚中兴等[10]对现存的通信自适应干扰对消系统进行了分析，并提出了提高干扰对消比的相关措施，宋文武等[11]对短波通信系统阻塞干扰的控制方法进行了研究，蒋云昊等[12～16]对自适应干扰对消系统进行了建模及性能分析，分析了多种非理想因素对系统性能的影响，并就斩波稳零下系统的性能进行了详细分析。文献[7～16]均是从干扰信号的角度出发，未分析系统对有用信号的影响，导致系统性能的评价指标不够完善。

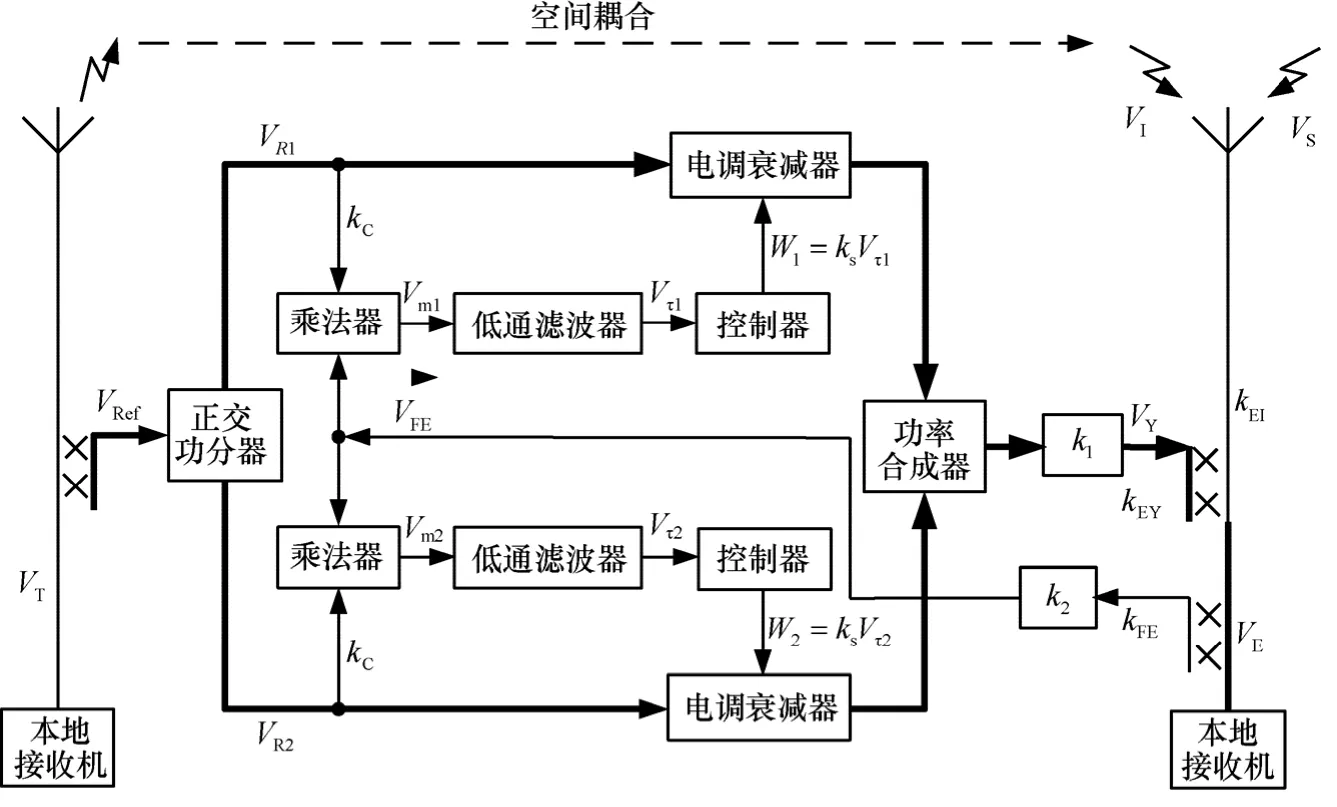
图1 自适应干扰对消系统

为更全面、有效地评价系统性能，完善对消系统理论，本文从时域角度对含有用信号的干扰对消系统进行了建模和理论分析，研究了“有用信号损耗”的特性，分析了有用信号损耗与干扰对消比、收敛时间的内在联系，给出了欠阻尼状态下，系统参数对系统性能指标的影响，最后，针对参数对有用信号损耗的影响进行了实验验证。

2 系统时域模型

自适应干扰对消系统如图1所示。假设参考信号为

干扰信号为

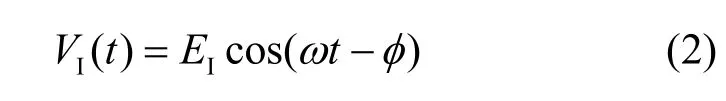
有用信号为

剩余信号为

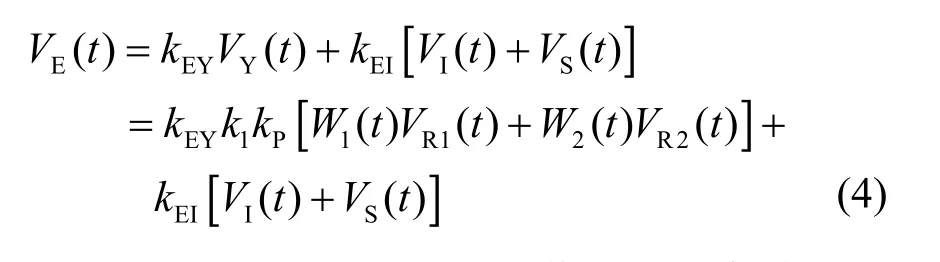
其中，ER、EI和 ES分别是参考信号（正交功分器前端）、干扰信号和有用信号的幅值，单位均为V；k1为放大器的放大倍数，W1(t)、W2(t)为权值控制支路产生的权值，VY(t)为加权输出的合成信号，kO为正交功分器的耦合系数，kP为功率合成器的系数，kEY与kEI分别是合成信号与接收信号的耦合系数。

设乘法器的“标准信号”为E0，则参考信号与剩余信号的乘积为

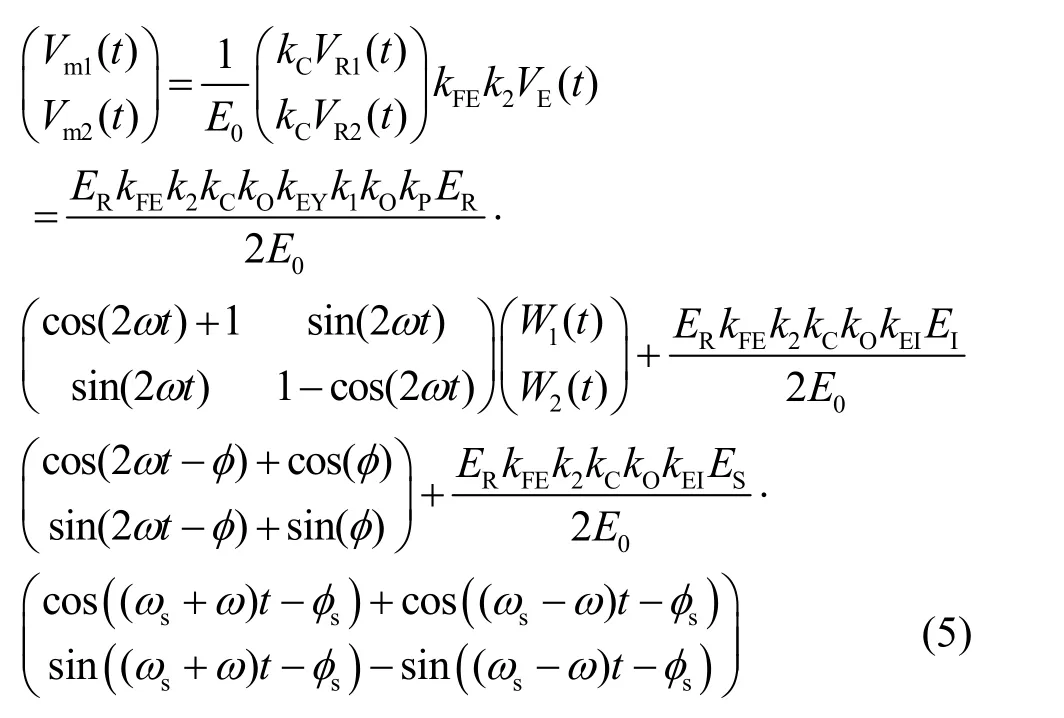
其中，kC为耦合器的耦合系数，kFE为误差反馈系数，k2为放大器的放大倍数。

一阶模拟低通滤波电路如图2所示，其输入输出满足表达式

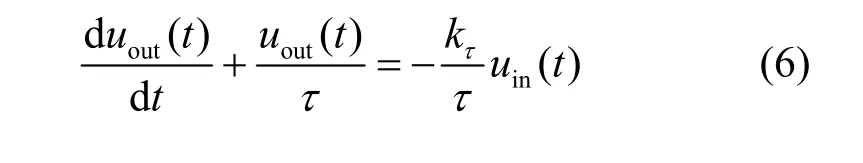
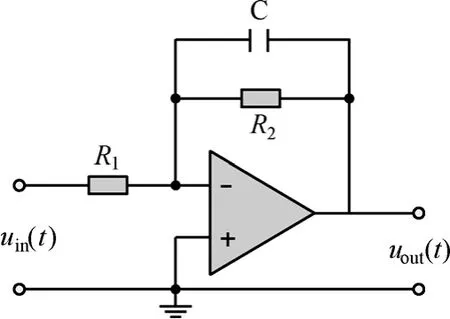
图2 采用放大器的一阶模拟低通电路

式(6)为一阶线性常系数微分方程。其中，时间常数 τ =R2C，直流放大倍数 kτ=R2/R1。

“乘积信号”经过“低通滤波”后，权值采用简单的“模拟”的“比例”控制方法

其中，kS为电调的控制特性参数，单位为V-1。

式(8)为变系数的微分方程组。其中，KVR=kskτkFEk2kCkO2kEYkPk1/E0， 单 位 为 V-2；KVI=kτkFEk2kCkOkEI/E0，单位为 V-1，均反映对消系统内部信号处理环节的特性。若忽略正负，则可称KVRER2/2 为系统的环路增益。

引入一个实正交对称矩阵

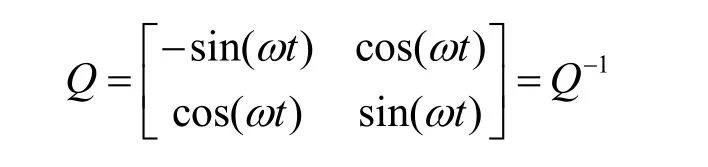
令

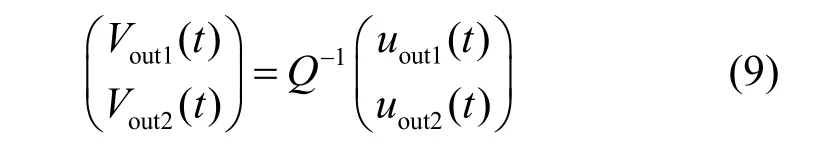
式(8)整理化简可得

式(10)为常系数的微分方程组。可求得系统的特征根为

由于特征根的实部恒为负数，所以对消系统是稳定的。

求解式(10)可得特解

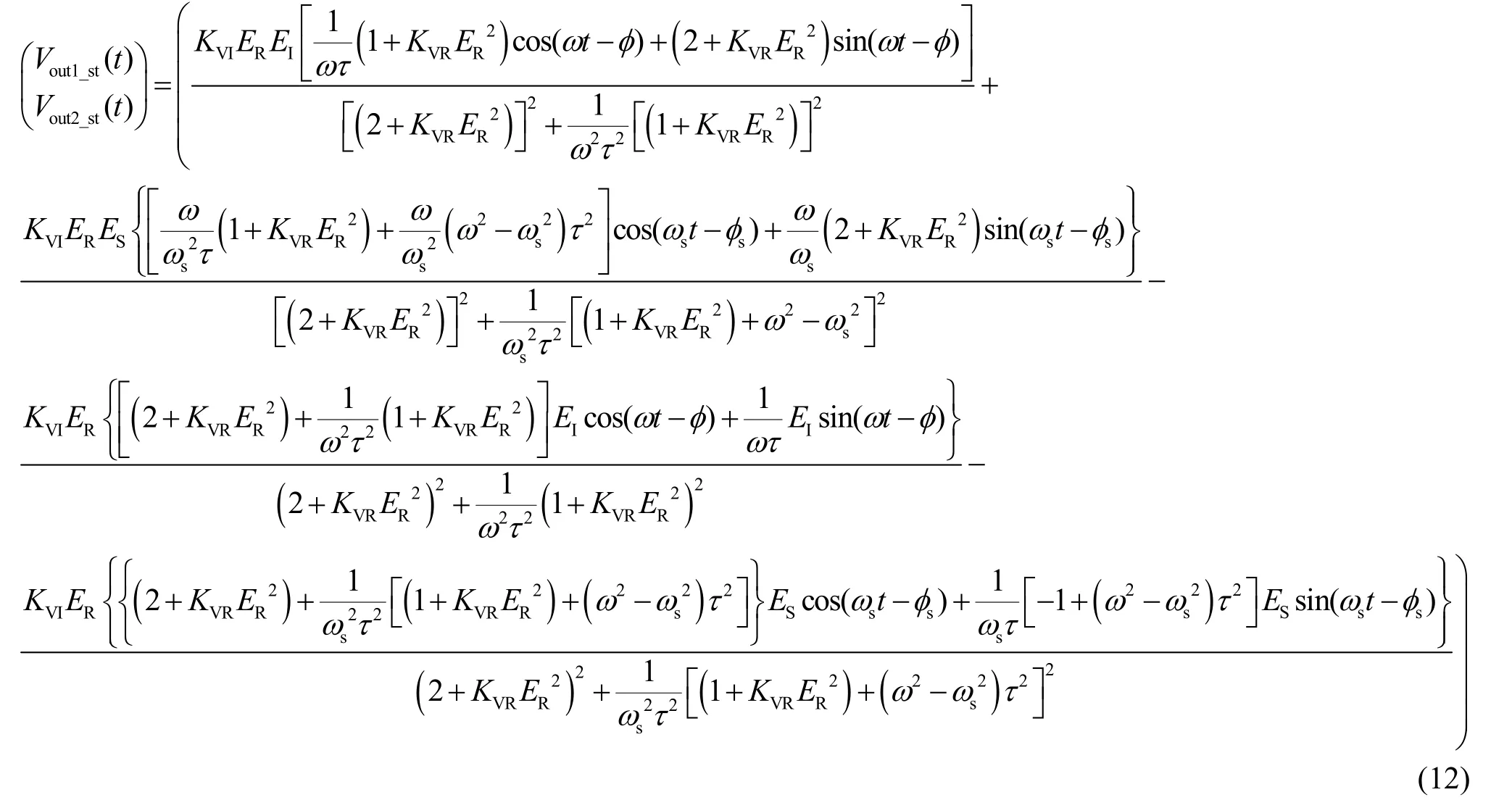
由式（4）、式（7）、式（9）、式（12）可得稳态剩余信号为

显然，稳态剩余信号包含干扰信号和有用信号2部分。其中，稳态剩余信号中的干扰信号为

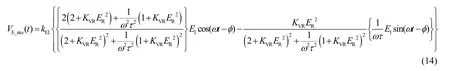
稳态剩余信号中的有用信号为

3 性能分析

3.1 暂态特性

根据特征根的特性，权值收敛的暂态过程分为欠阻尼、临界阻尼和过阻尼3种状态。

对消系统暂态过程的收敛时间满足

图3给出了对消系统的收敛时间特性，可以看出，临界阻尼状态时的收敛速度最快；欠阻尼状态下，对于同一时间常数 τ，环路增益 KVRER2/2越大，收敛速度越快，且收敛速度与干扰频率f无关；过阻尼状态下，对于同一时间常数τ，环路增益 KVRER2/2越大，收敛速度越慢，且收敛速度与干扰频率f有关，干扰频率f越高，收敛速度越快。

图3 对消系统的收敛时间特性

3.2 稳态特性

定义干扰对消比

定义有用信号的损耗为

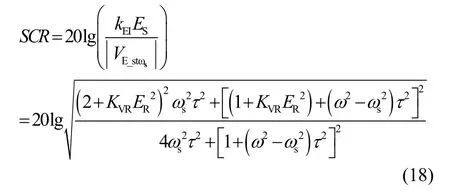
对消系统要消除强干扰，则必须要有较大的干扰对消比ICR，但同时对有用信号损耗SCR应尽量小。图 4给出了干扰信号频率为2.5MHz、有用信号频率及低通时间常数改变时，干扰对消比与有用信号损耗的特性。

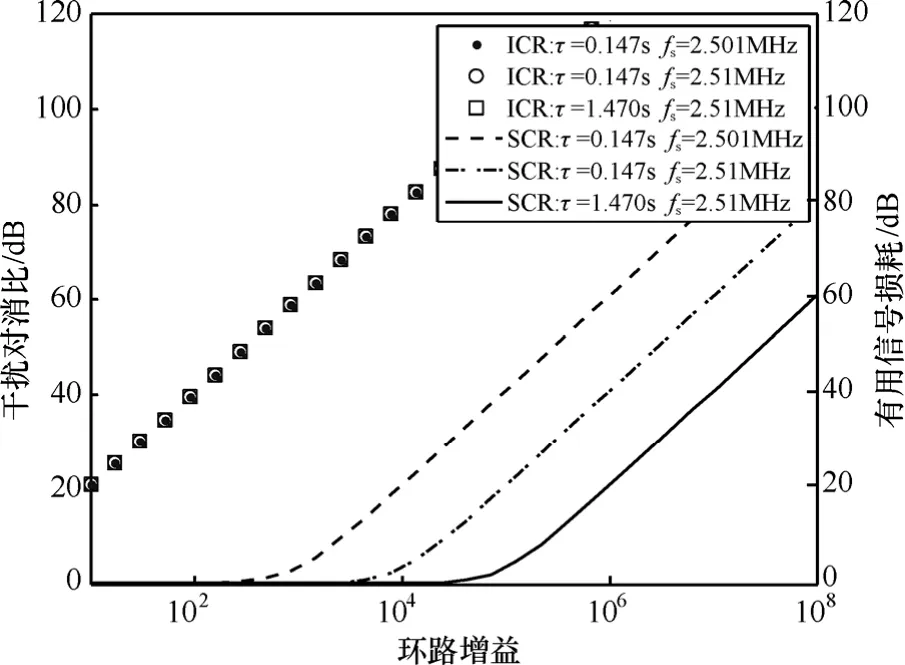
图4 干扰对消比与有用信号损耗特性

由图4可以看出，干扰对消比主要受环路增益KVRER2/2的影响，环路增益越大，干扰对消比越大；与 ωτ基本无关。但环路增益越大，有用信号损耗SCR越大；时间常数τ越大，有用信号损耗SCR越小；有用信号与干扰信号的频率间隔| fs-f |越大，有用信号损耗SCR越小。

当 KVRER2/2＞＞1 且 ω2τ2＞＞1 时，式(17)可近似为

当 KVRER2/2 ＞＞ 1、| fs-f |≥100Hz 且 τ≥0.1s时，显然 ω2τ2＞＞1，式(18)可近似为

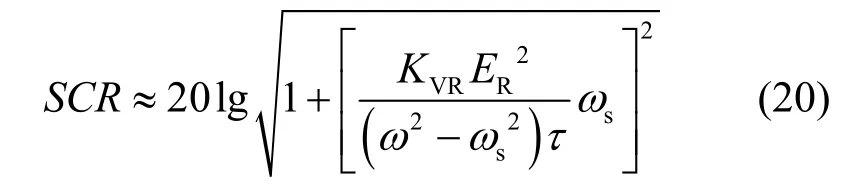
3.3 参数优化准则

权值收敛的暂态过程分为欠阻尼、临界阻尼和过阻尼3种状态，临界阻尼状态时的收敛速度最快，对比稳态特性分析，可以看出临界阻尼状态时，有用信号损耗较大，过阻尼状态时的有用信号损耗更为严重，由式(20)可得临界阻尼状态时的有用信号损耗为

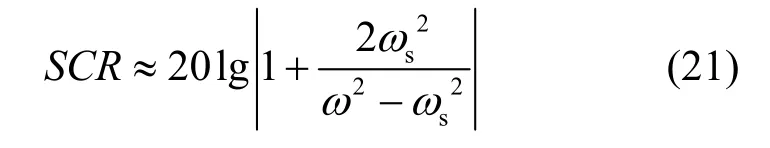
当干扰信号频率为 2.5MHz，有用信号频率为2.51MHz时，临界阻尼状态时的有用信号损耗约为48dB，且频率间隔| fs-f |越小，有用信号损耗越大。因此，实际的对消系统反馈电路只能工作在欠阻尼状态。

表1给出了欠阻尼状态下参数对系统性能指标的影响。需要注意的是，在分析某一个参数的影响时，假定其他参数不变（KVR与τ是关于R2耦合的，KVR变化时应保持R2不变；τ = R2C变化是通过调节C实现的）。通过上述分析，可以看出：干扰对消比、收敛速度均与有用信号损耗相互制约，因此，在系统设计时，需根据系统性能指标折衷考虑。

表1 欠阻尼状态下，参数对系统性能指标的影响

4 实验验证

为验证理论分析的正确性，进行了含干扰信号和有用信号的干扰对消实验，实验平台如图5所示，其中，信号源1产生参考信号和干扰信号，频率为2.5MHz，幅值可调；信号源2产生有用信号，频率、幅值可调。实验平台中采用了课题组初期研发的对消装置，其相关参数为：E0=1、kC=0.063 1、kO=kP=kEY= kEI=0.707、kS=4、k1=2、k2=9.091、kFE=0.281 8、kτ=196.08，即KVR=63.39。参考信号幅值ER可变。

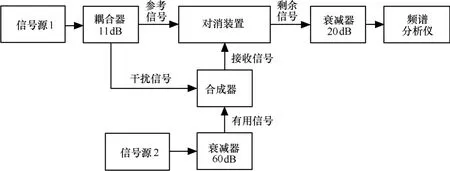
图5 干扰对消系统实验平台

通过改变参数系统环路增益KVRER2/2、低通时间常数τ 、频率间隔| fs-f |来观测有用信号和干扰信号的变化，其中，KVR=63.39，f=2.5MHz。实验数据如表2、表3所示。

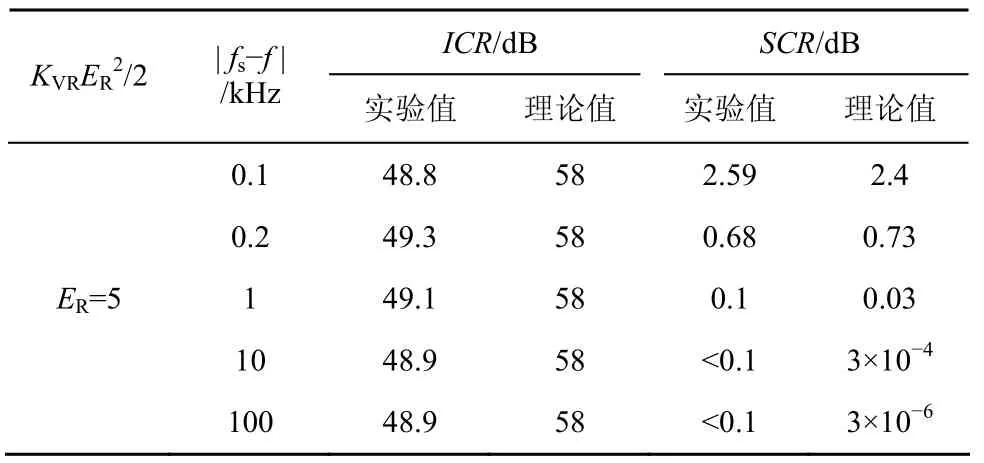
表2 ICR与SCR实测数据(τ =1.47s)

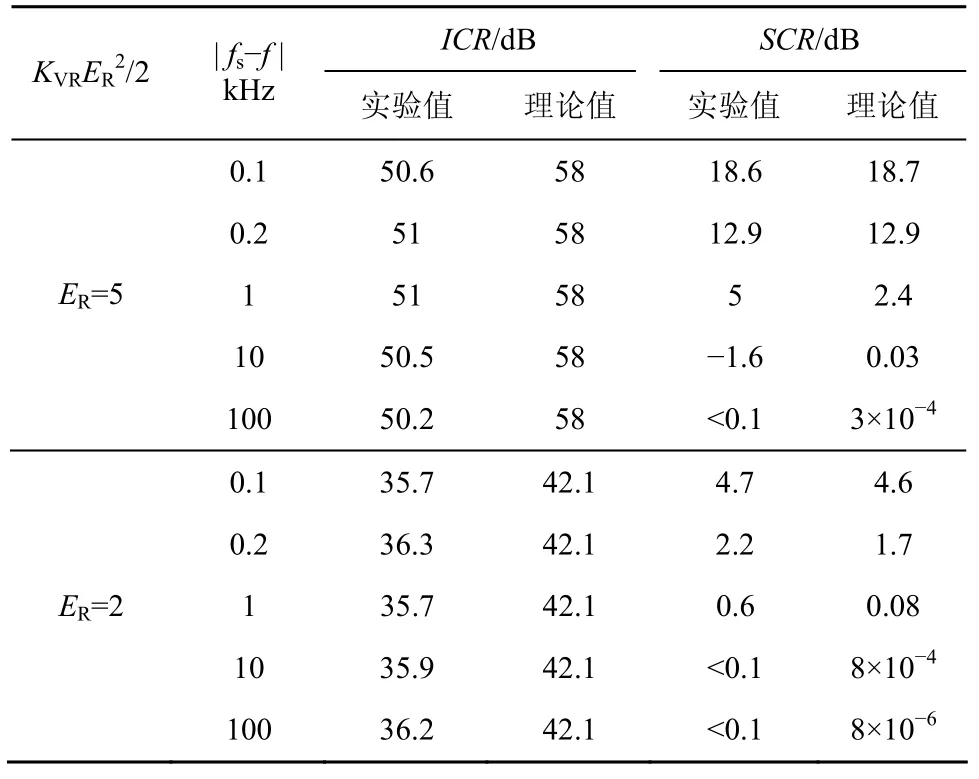
表3 ICR与SCR实测数据(τ =0.147s)

图6和图7是表3中参数为低通时间常数τ=0.147s、环路增益 KVRER2/2=63.39×52/2、频率间隔| fs-f |= 1kHz时，干扰对消前后实验测试的频谱图。由图可以看出，对消前干扰信号功率为-14.6dBm，有用信号功率为-83.05 dBm；对消后干扰信号功率为-65.58dBm，有用信号功率为-88.01 dBm，干扰对消比约为51 dB，有用信号损耗约为5dB。

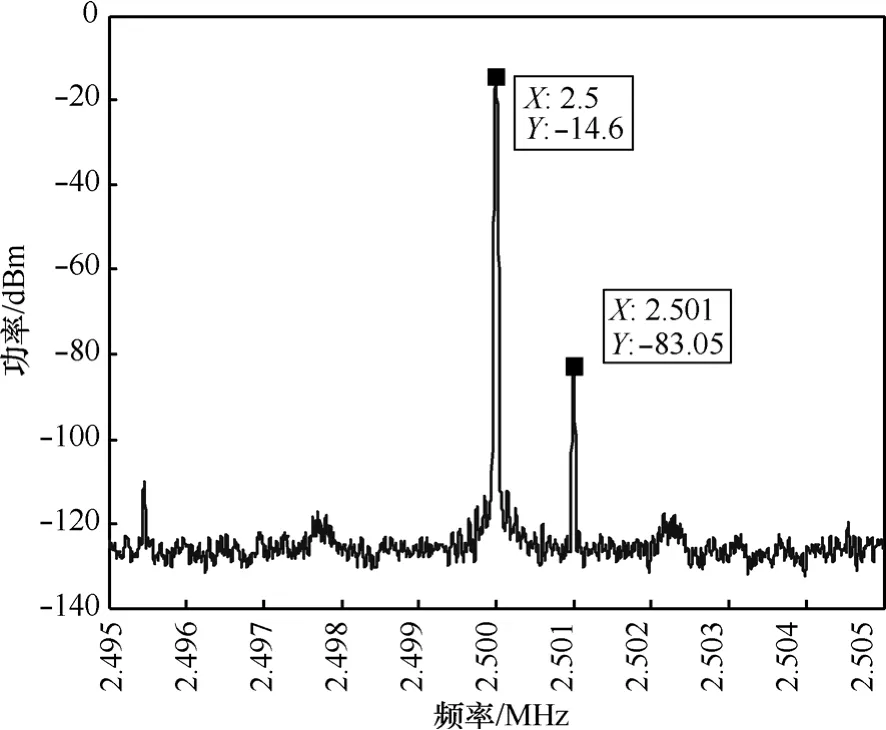
图6 对消前频谱

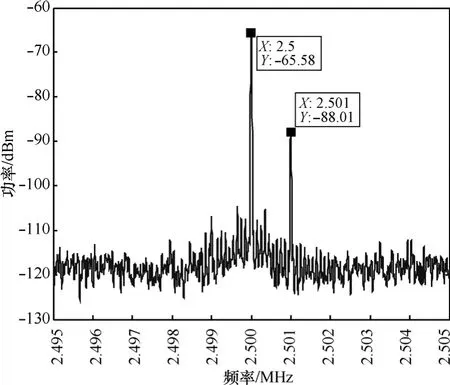
图7 对消后频谱

由表2、表3可以看出：

1) 有用信号损耗的实验值与理论值是基本吻合的，验证了理论的正确性。当参数为 τ = 0.147s、KVRER2/2=63.39×52/2、| fs-f | = 10kHz时，有用信号损耗与理论分析不符，这主要是由于电调控制系统对于10kHz以上的信号具有较大的附加时延，较高频率| fs-f |控制信号的相位特性与理论分析不符合。需要注意的是，随着频率| fs-f |的增高，由于低通的衰减特性，对消系统对有用信号的影响可忽略不计。

2) 干扰对消比实验值比理论值偏低，这是因为实际的干扰对消系统中存在非理想因素，其中，干扰对消比受零漂的影响较大[9,16]。从参考支路信号合成的角度来看，合成的干扰信号主要由权值的直流成分与参考信号相乘得到，而合成的有用信号由权值中的| fs-f |分量与参考信号相乘得到，由于零漂可近似认为一个较小的直流量叠加到权值中，所以零漂对干扰信号有较大影响，而对有用信号的影响可忽略不计。

3) 系统环路增益 KVRER2/2增大，干扰对消比增大，但有用信号损耗也会增大。此时，可以通过增大时间常数τ和增大频率间隔来降低系统对有用信号的影响。在实际的对消系统设计时，首先要保证有用信号损耗较小，确保接收系统对有用信号的正确处理，在这个前提条件下，再考虑干扰对消比和收敛时间的优化设计。

5 结束语

本文对含有用信号的自适应干扰对消系统性能进行了时域分析，研究了“有用信号损耗”的特性，实验结果验证了理论分析的正确性，为对消系统的优化设计提供了重要的理论依据。本文主要结论如下：

1) 考虑到有用信号的损耗，对消系统的反馈电路需工作在欠阻尼状态。

2) 得到了有用信号损耗与干扰对消比、收敛速度之间的内在联系，给出了参数优化的准则。

3) 零漂对有用信号损耗基本无影响，但零漂对干扰对消比影响较大，所以仍需对零漂进行有效抑制。

4) 在实际的短波系统中，频率间隔| fs-f |一般大于10kHz，虽然电调控制系统对于10kHz以上的信号具有较大的附加时延，但是通过优化系统参数，即环路增益KVRER2/2和低通时间常数τ，则可保证系统对有用信号的影响可忽略不计，又可以实现较高的干扰对消比和较快的收敛速度。

[1] WIDROW B, GLOVER J R, MCCOOL J M. Adaptive noise cancelling： principles and applications [J]. Proc IEEE, 1975, 63(12)： 1692-1716.

[2] ANDREWS D C, BARR E E, OLVER T E, et al. Linear wideband hf power amplifier using adaptive feedback cancellation[A]. IEEE Military Communications Conference[C]. Boston, USA, 1982. 1-8.

[3] ADRIAN S E. Performance of alternative adaptive interference canceller configurations in a shipboard environment[A]. IEEE Military Communications Conference[C]. Washington D C USA, 1983.537-543.

[4] TRAVIS G W, LENZING H F. Shipboard HF interference： problems and mitigation[A]. IEEE Military Communications Conference[C].Boston, USA, 1989. 106-110.

[5] KIM S J, LEE J C, LEE J H, et al. Adaptive feedback interference cancellation system[A]. IEEE MTT-S International Microwave Symposium Digest[C]. Philadelphia, USA, 2003. 627-630.

[6] NIGHTINGALE S J, SODHI G S, AUSTIN J E, et al. An eight channel interference cancellation system[A]. IEEE MTT-S International Microwave Symposium Digest[C]. San Francisco, CA, 2006. 914-917.

[7] 杜武林.干扰抵消技术的原理和应用[J]. 电信科学, 1988, 4(5)：51-55.DU W L. Principle and application of interference cancellation technology[J]. Telecom Science, 1988, 4(5)： 51-55.

[8] 马义广，杜武林. 自适应干扰抵消系统的性能分析与设计[J]. 西安电子科技大学学报, 1992, 19(1)： 84-92.MA Y G, DU W L. Performance analysis and design of adaptive interference canceling system [J]. Journal of Xi’dian University, 1992,19(1)：84-92.

[9] 郑伟强, 杜武林. 自适应干扰抵消研究[J]. 电讯技术, 1991,31(6)：20-27.ZHENG W Q, DU W L. Study of adaptive interference canceling [J].Telecommunication Engineering , 1991, 31(6)：20-27.

[10] 姚中兴, 李华树, 任桂兴. 通信自适应干扰对消系统的性能分析[J].西安电子科技大学学报, 1995, 22(3)： 256-261.YAQ ZH X , LI H SH , REN G X. Performance analysis of adaptive interference cancellation system in communication[J]. Journal of Xi’dian University, 1995, 22(3)： 256-261.

[11] 宋文武, 丁志尧, 张凯. 短波通信系统阻塞干扰控制方法研究[J].装备环境工程, 2010, 7(2)： 68-70.SONG W W, DING Z Y，ZHANG K. Study of controlling of barrage jamming of shortwave communication system[J]. Equipmient Environmental Engineering, 2010,7(2)： 68-70.

[12] JIANG Y H, MA W M, ZHAO Z H. The analysis of an adaptive sinusoidal interference cancellation system[A]. Proceedings of the 11th International Conference on Electrical Machines and Systems[C].Wuhan, China, 2008. 640-645.

[13] JIANG Y H, MA W M, ZHAO Z H. Influence of non quadrature of phase shifter to adaptive interference cancellation system[A]. International Conference on Intelligent Human-Machine Systems and Cybernetics[C]. Hangzhou, China, 2009. 359-363.

[14] JIANG Y H, MA W M, ZHAO Z H. Adaptive interference cancellation system with different correlation control methods[A]. International Conference on Intelligent Human-Machine Systems and Cybernetics[C]. Hangzhou, China, 2009. 372-375.

[15] 蒋云昊，马伟明，赵治华. 斩波稳零下自适应干扰对消系统的性能分析[J]. 通信学报, 2010, 31(3)： 65-74.JIANG Y H, MA W M, ZHAO Z H. Analysis of chopping stabilizing zero for adaptive interference cancellation system[J]. Journal on Communications, 2010, 31(3)： 65-74.

[16] JIANG Y H, ZHAO Z H, HU A Q, et al. Influence of different gains to adaptive interference cancellation system[A]. Asia-Pacific International Symposium on Electromagnetic Compatibility[C]. Beijing,China, 2010. 1394 -1397.