供应链中基于蚁群算法的供应商选择研究

胡小建，常光辉，宫飞翔

（1.合肥工业大学管理学院，安徽，合肥 230009；2.过程优化与智能决策教育部重点实验室，安徽，合肥 230009）

供应商选择的研究大致经历了3个阶段：早期的定性方法研究；随后的定量方法研究；以及定性与定量相结合的方法研究。早期的定性研究方法主要有直观判断法和协商选择法[1]。1915年由美国的电气工程师Harris首次提出经济批量（Economic Order Quantity，EOQ）模型后，人们从定性方法开始转向采用定量方法来选择供应商，目标是减少采购的经济批量以减小采购成本。不久，人们注意到影响供应商选择有很多因素[2]，只从库存和采购成本的角度选择供应商是不够的，从而人们将定性与定量方法相结合来研究供应商的选择。供应商选择其实质是一个多目标决策问题。目前，关于供应商选择的决策模型及方法主要有ABC成本法、多目标数学规划法、层次分析法（AHP）、模糊综合评判法[3-4]、TOPSIS法、灰色综合评价法等。结合这些已有的研究方法与现有的决策理论方法解决供应商选择问题成为研究热点。

Chaudhryetal[5]用整数规划方法分析了带权重的供应商选择，用数学方法解释了由多个商业规划软件工具算出的整体价格总比由一个商业规划软件工具算出的结果好。Zeger Degraeve 等[6]以总拥有成本计算方法建立了供应商的选择模型，并以钢铁行业的某跨国公司为研究对象进行分析，验证了该模型的正确性。Marcello Braglia[7]使用数据包络分析（DEA）的方法帮助采购人员在不断变化的市场中制定可行的采购方法。P.K.H等[8]考虑到环境因素对供应商选择的影响，提出了一种基于环境因素的供应商选择框架。Cengiz Kahraman等[9]使用模糊层次分析法（F-AHP）建立了供应商选择模型。

我国的孔原[10]从技术、协作、服务等多方面对供应商选择进行评估，提出了基于BP神经网络的供应商评价方法，并说明了供应商选择实质是一个多目标决策问题。马祖军[11]将伙伴联盟的概念运用在了供应链中，描述了在多目标供应链联盟中的伙伴选择问题，提出了一种基于自适应遗传算法求解供应链联盟伙伴选择问题。蒋建国、夏娜[12]在基于蚁群算法的敏捷供应链伙伴选择问题中，提出了一种基于蚁群算法的敏捷供应链伙伴选择优化算法，并通过大量仿真试验验证了该方法的有效性。董景峰[13]分析了传统供应商选择只是针对单一物资供应过程和面向单一供应商选择存在的局限性，提出了基于改进蚁群算法的多供应商选择问题解决方法，并通过大量的仿真试验证明了该方法在解决多任务和多供应商选择问题上是正确合理的。

综上所述，关于供应链中供应商的选择问题研究已经取得了很大的成果，供应链管理合作方式在发掘企业盈利潜能上的作用极大地促进了供应链在实践中的应用。然而，供应商选择是一个多指标权衡的过程，企业针对不同的产品或原材料可能会对供应商的指标评价权重不同，有的企业更看重产品质量，有的企业则重点考虑产品成本。当产品数量越多、备选供应商规模越大，将供应商自身的指标和企业对产品的需求情况同时考虑进行选择时，将是一个复杂的组合优化问题。为此，本文引入蚁群算法来解决这一问题，通过多次仿真试验得出适合问题的最优参数值，同时为了避免算法较早陷入局部最优，本文还对基本的蚁群算法做了改进，加入了启发式因子的“扰动策略”。最后，通过某汽车制造企业的简单实例证明了本文所建立的供应商选择模型与求解算法是合理有效的。

1 模型建立

1.1 模型的提出

传统的供应链管理中，供应商的选择主要以价格为评价指标，选取价格为评价指标往往会造成供应链不稳定，最终会使产品质量和服务水平下降[14]。现代供应链更强调稳定性，即从长远的角度建立供应链战略伙伴，因此，在选择供应商时不能仅仅从价格的角度考虑，选择合理的评价指标对供应链中供应商选择至关重要，通常选择时间、质量、价格、交货期与交货提前期作为供应商选择的评价指标[15]。

表1 供应商指标

其中，价格指供应商采购某种原材料的价格；运输成本指供应商企业运输原料从原料供应地到下一个目的供应商的总费用；质量指产品满足企业需要的程度或者满意度，通常用废品率表示；交货期指产品在满足企业需求的前提下完成订单的时间；交货提前期是指供应商实际交货的时间比计划交货时间提前的时间。对企业来说，交货提前期越大越好。

综上所述，该问题可形式化描述为：现需要某种物资Ai，从备选的若干个供应商中选择其中的几个供应商作为物资的货源，使其物资成本最低，一方面使参与的企业满意，另一方面使消费者购买时的价格最低，使上述各项指标参数达到最优。该问题属于多目标决策问题。

1.2 模型建立

对指标进行无量纲修正，如下：

式中：Spmax、Spmin，Scmax、Scmin，Sqmax、Sqmin，Stmax、Stmin，Samax、Samin分别为价格指标的最大值和最小值，运输成本指标的最大值和最小值，质量指标的最大值和最小值，交货期指标的最大值和最小值，交货提前期的最大值和最小值。

修正后的指标之和就是模型的评判函数，即

选择供应商的最优结果就是评判函数的最小值。

由于企业对产品或原材料的要求不同，会对供应商各指标的权重[16]有所不同，下面对模型做进一步扩展。

设企业根据产品或原材料给出的指标权重系数集为

定义1 指标无量纲修正矩阵

根据指标评价权重系数对每一个指标的修正值乘以相应的权重系数得到最终的带有评价权重的指标无量纲修正值。

定义2 带有指标评价权重系数的无量纲修正矩阵

式中：E为单位矩阵，求F得最小值是最终目标。

2 问题求解

2.1 问题图形表示

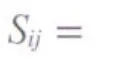
2.2 基于基本蚁群算法的供应商选择

蚁群算法[17-18]是受到自然界中的蚂蚁行为的启发而提出的，是由意大利学者Dorigo等人首先提出，大量研究已经初步证明蚁群算法作为一种新的启发式优化算法，具有较强的鲁棒性、优良的分布式计算机制等特点，在求解组合优化问题上有显著效果。

完成一次迭代后，每条待选线路的信息素被更新为

2.3 算法的改进

如果蚂蚁多次循环后找到一组供应商，蚂蚁在这些供应商节点的信息素浓度就高，则在下一次循环蚂蚁仍会倾向于选择这些供应商，体现了“熟人机制”[19]，导致没有被选中的节点的信息素不断挥发，最后为0。为了避免在搜索过程中某些节点被“遗忘”，而出现算法停滞，我们采取一种“扰动策略”，其主要思想是当算法出现停滞时即认为已经找到最优解，此时的目标函数值F最小，被选中的节点上的信息素浓度均高于其它的节点，在蚂蚁下一次循环时减小响应节点的启发式因子α，因此，状态转移概率更新为

式中：c为扰动因子，当N次循环最优解没有明显改进时，EVij/Fk为一定值，此时引入c来改变EVij/Fk的值，从而改变α的值，对信息素进行改变。

2.4 算法描述

步骤2 初始化参数：α，β，τij(0)，ρ，N，Q，设置最大循环次数Nmax。

步骤3 按照图1随即放入n只蚂蚁到供应链的第1类供应商节点上。

步骤4 for k=1 to R

按照改进的具有“扰动策略”的状态转移概率公式（11）计算，并设c=1，选择出下一类供应商节点。

步骤5 当蚂蚁遍历完所有节点时，一次循环结束，根据式（6）计算当前的Fk值。

步骤6 If（Fk==N个循环以前的最小目标函数值）

thenc ++

步骤8 If Nc＜Nmaxthen

清空禁忌表中的数据，

Nc=Nc+1

转至步骤4

Else

输出最优解

End If

3 算例及试验分析

为了验证上述供应商选择的数学模型及求解算法的正确性与合理性，以某汽车制造公司采购配件为例，假设该公司欲求购一批配件（共4种），分别为A1，A2，A3，A4。有足够生产能力满足其需求的供应商数量为7家，分别为S1，S2，S3，S4，S5，S6和S7，欲从中选出3家供应商采购配件。为便于采购管理与双方经济利益，决定每种配件只由1个供应商供应，但1个供应商可同时供应多种配件。对各供应商的评价指标无量纲修正后分别为

V1=[0.621,0.187,0.426,0.789,0.438]T，

V2=[0.857,0.433,0.167,0.451,0.688]T，

V3=[0.364,0.636,0.375,0.583,0.778]T，

V4=[0.526,0.923,0.756,0.781,0.000]T，

V5=[0.481,0.000,0.923,0.902,0.857]T，

V6=[0.500,0.364,0.636,0.273,0.429]T，

V7=[0.583,0.173,0.778,0.526,0.192]T.

企业根据配件的属性由专家评分法得到这4种配件的指标评价权重系数分别为

W1={0.28,0.12,0.46,0.08,0.06}，

W2={0.13,0.32,0.40,0.12,0.03}，

W3={0.08,0.07,0.38,0.32,0.15}，

W4={0.35,0.26,0.25,0.05,0.09}.

根据式（5）计算得到4类带有指标评价权重的指标修正值集。

按照上述算法即从这4类集合中选出3个节点，使其总指标值最小。该算法的关键在于选取适当的参数，从式（11）中可以看出，α值越大，蚂蚁的转移概率越大，但是α值过大会使算法极易陷入局部搜索，产生局部最小值；β值的大小反映了启发式信息受重视的程度；参数ρ表示蚂蚁残留信息素的保留程度，其大小影响算法的收敛速度，过大则残留信息素“挥发”过慢，算法极易产生停滞现象，过小则残留信息素“挥发”过快，导致较好的结果不易发现。本文通过试验确定合适的参数值，图2是本算法中的3个参数α、β和ρ分别对算法性能的影响曲线。从图中可以看出，α=0.5，β=8，ρ=0.4 是较合理的选择。

综上所述，n=7，m=4，u=3。其它常量初始化为 α=0.3，β=10，ρ=0.5，Q=10；τmn（0）=0.01，Nmax=100，mant=20。以Matlab为仿真平台应用文章的算法对汽车公司采购配件的实例进行试验得到结果如图3所示。

由图3（a）可知，处于第1类的第2个节点S2的目标值最小，因此由供应商S2供应配件A1；第2类和第3类的都是第4个节点S4的目标值最小，则由供应商S4供应配件A2和A3；第4类的节点S6供应配件A4。并由图3（b）可以看出，蚂蚁经过100次循环得到最终的目标最优值为1.2。

为了验证本文改进的蚁群算法具有较好的搜索能力和收敛速度，将上述问题用基本的蚁群算法进行求解，同时与本文算法进行比较，同样参数设置为α=0.3，β=10，ρ=0.5，初始放置20只蚂蚁，循环100次后的结果如图4所示。

图4中，改进后的蚁群算法经过50次的循环搜索后基本达到了最优目标值，基本的蚁群算法在寻优过程中始终比改进的算法慢，经过近70次的循环后才基本达到稳定阶段，并且得到的结果略高于最优目标值。由此可以看出本文经过改进后的蚁群算法是有效的。

4 结论

本文考虑到企业对不同产品的需求情况会对选择供应商的指标评价权重产生影响，将供应商评估指标和产品对指标评价权重系数相结合，建立了供应商选择的数学模型，并构造了适合问题的改进的蚁群算法。由于蚁群算法在求解过程中容易陷入停滞状态，为此本文对基本的蚁群算法做了改进，对启发式因子做了扰动策略。通过试验证明了本文提出的模型的合理性和算法的有效性，为企业进行供应商选择提供了一种更为符合实际的方法，对供应链管理有很好的实用价值。

[1]马士华，林勇.供应链管理[M]. 北京：机械工业出版社，2005.Ma Shihua，Lin Yong. Supply Chain Management[M].Beijing：China Machine Press，2005.（in Chinese）

[2]龚月琴，累勋平. 供应商选择研究[J].物流技术，2006(3)：174-176.Gong Yueqin，Lei Xunping. Research on Supplier Selection[J]. Logistics Technology，2006(3)：174-176. （in Chinese）

[3]边利，李自如.供应商选择的模糊多目标最优决策与实证研究[J].科技管理研究，2006(3)：224-226.Bian Li，Li Ziru. Supplier Selection Model Based on Fuzzy Multi-objective Optimum Decision Making and Empirical Study[J]. Science and Technology Management Research，2006(3)：224-226. （in Chinese）

[4]赵小惠，孙林岩.供应链中供应商选择模糊方法[C]//第1届国际机械工程学术会议论文集，北京：机械工业出版社，2000：12-15.Zhao Xiaohui，Sun Linyan. A Fuzzy Method for Supplier Selection in Supply Chain Management[C]//The First International Conference on Mechanical Engineering，Beijing：Mechanicl Industry Press，2000：12-15.（in Chinese）

[5]Bi Weining，Ru Qinyao. Supplier Evaluation and Selection via Taguchi Loss Functions and an AHP [J].International Journal of Advanced Manunfacturing Technology，2006(27)：36-39.

[6]BAYAZIT O，KARPAK B，YAGCI A.A Purchasing Decision：Selecting a Supplier for a Construction Company [J]. Journal of Systems Science and Systems Engineering，2006，15(2)：217-231.

[7]刘晓.基于供应链的供应商选择模型与算法[J].仪器仪表学报，2005(8)：890-892.Liu Xiao. Models and Method for Supplier Selection Based on Suppluy Chain[J]. Chinese Journal of Scientifie Instrument，2005，26(8)：890-892.（in Chinese）

[8]GHODSYPOUR， BREIEN C O. A Decision Support System for Supplier Selection Using an Integrated Analytic Hierarchy Process and Linear Programming[J]. International Journal of Production Economics，1998(56-57)：199-212.

[9]FENG W D， CHEN J，ZHAO C J. Partner Selection Process and Optimization Model for Virtual Corporations Based on Genetic Algorithms [J].Journal of Tsinghua University (Sci & Tech)，2000，40(10)：120-124.

[10]孔原，刘览.基于BP神经网络的供应商评价方法研究[J].价值工程，2007(6)：89-92.Kong Yuan，Liu Lan.The Method Research about the Supplier Appraises Based on BP Neural Network[J].Value Engineering，2007(6)：89-92.（in Chinese）

[11]马祖军.基于遗传算法的供应链联盟伙伴选择[J].系统工程理论与实践，2003(9)：81-84.Ma Zujun.Partner Selection of Supply Chain Alliance Based on Genetic Algorithms[J].Systems Engineering Theory and Practice，2003(9)：81-84.（in Chinese）

[12]蒋建国，夏娜，张国富，等.基于蚁群算法的敏捷供应链伙伴选择[J]. 系统仿真学报，2006(12)： 3377-3379.Jang Jianguo，Xia Na，Zhang Guofu，et al. Partner Selection of Agile Supply Chain Based on Ant Colony Optimization Algorithm [J]. Journal of System Simulation，2006(12)：3377-3379. （in Chinese）

[13]董景峰，王刚，吕民，等. 基于改进蚁群算法的多供应商选择问题求解[J].计算机集成制造系统，2007(8)：1639-1644.Dong Jingfeng，Wang Gang，Lü Min，et al.Mutisupply Selection Problem Solution Based on Improved Ant Colony Algorithm[J]. Computer Integrated Manufacturing System，2007(8)：1639-1644. （in Chinese）

[14]谢君，胡容兵.供应链的合作伙伴选择方法综述[J].价值工程，2005(1)：43-46.Xie Jun，Hu Rongbing. Supply Chain Partner Selection Method [J]. Value Engineering，2005(1)：43-46. （in Chinese）

[15]刘晓，李海越，王成思.供应商选择模型与方法综述[J].中国管理科学，2004(12)：139-147.Liu Xiao，Li Haiyue，Wang Chengsi. Survey of Supplier Selection Model[J]. Chinese Journal of Management Science，2004(12)：139-147. （in Chinese）

[16]杨和雄，李崇文.模糊数学和它的应用[M].天津：天津科技出版社，1990.Yang Hexiong，Li Chongwen. Fuzzy Mathematics and Its Application[M].Tianjin：Tianjin Science and Technology Press，1990. （in Chinese）

[17]胡小兵，袁锐，黄席樾，等. 蚁群算法原理的仿真研究 [J]. 计算机仿真， 2004(8)：125-127.Hu Xiaobing，Yuan Rui，Huang Xiyue，et al.Simulation Research on the Principle of Ant Colony Algorithm [J]. Computer Simulation， 2004(8)：125-127. （in Chinese）

[18]DORIGO M，STUTZLE T. Ant Colony Optimization[M].U.S：MIT Press， 2004.

[19]段海滨，王道波.一种快速全局优化的改进蚁群算法及仿真[J].信息与控制，2004，33(2)：241-244.Duan Haibin，Wang Daobo. A Fast Global Optimization Ant Colony Algorithm and Its Simulation [J]. Information and Control，2004，33(2)：241-244. (in Chinese)