蜂窝梁挠度的简化计算

张兴杰

(机械工业第三设计研究院，重庆400039)

蜂窝梁通常由H形型钢或工字形型钢切割后错位相焊制成。具有自重轻、承载能力高、经济、美观等优点，在实际工程中的应用可以带来显著的经济效益。

1 理论公式推导

目前蜂窝梁的强度计算比较成熟，且计算公式也列入了相关规范。但在挠度计算方面，国外规范中基本上都采用估算法，精度较低，而且现有的较为精确的挠度计算式均把腹板孔洞简化为四边形孔，与实际状况差异较大。

本文以费氏空腹桁架计算理论为基础，即认为在外荷作用下，蜂窝梁桥的中点和墩腰处均为反弯点，从而把多次超静定结构简化为静定结构来计算，其物理概念清楚，计算也较为方便。故采用三项挠度理论来推导两端简支正六边形孔蜂窝梁在均布荷载和跨中集中荷载作用下，跨中挠度的理论计算式。

蜂窝梁的挠度应由三部分组成:

式中:fM为仅因弯矩产生的挠度;

fQ为仅因剪力产生的挠度;

fe为仅因剪力引起的次弯矩产生的挠度。

假定蜂窝梁由图1所示的制作方法制成，原工字形截面钢梁的截面高度为H，加工后蜂窝梁截面高度为h，则扩张比K=h/H。加工后蜂窝梁翼缘板厚度为t，翼缘板宽度为b，腹板高度为hw，腹板厚度为tw，腹板正六边形孔洞边长为a(图2)，钢材弹性模量为E，剪切模量为G。为了便于计算，将标准孔段分成1、2、3、4区段，并令孔洞数为偶数。

图1 蜂窝梁构造

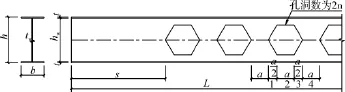
图2 蜂窝梁尺寸

1.1 跨中集中荷载作用下的跨中挠度

1.1.1 弯矩挠度fM

(1)梁端实腹部分

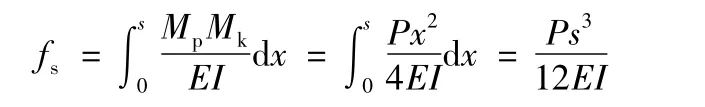
(2)孔洞1区

由于积分出来的式子过于复杂，故直接利用积分定义编制BASIC程序求得该式结果(下同)。

(3)孔洞2区

(4)孔洞3区

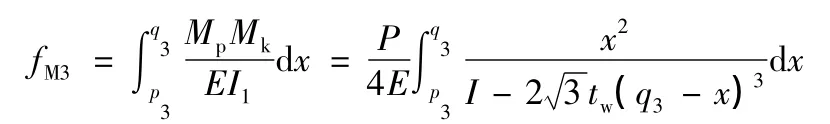
(5)孔间4区

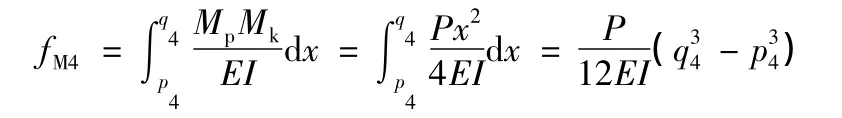
(6)跨中部分

则，最终由弯矩引起的挠度即为:

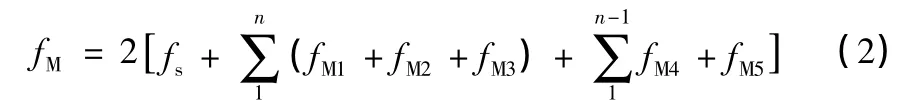
1.1.2 剪力挠度fQ

(1)梁端实腹部分

式中:ks为剪力不均匀系数。

(2)孔洞1区

由于积分出来的式子过于复杂，故直接利用积分定义编制BASIC程序求得该式结果(下同)。

(3)孔洞2区

(4)孔洞3区

由于在跨中集中荷载作用下梁上各处剪力大小均相同，故该部分剪力产生的挠度与fV1相同。

(5)孔间4区

(6)跨中部分

则，最终由弯矩引起的挠度即为:

1.1.3 剪力次弯矩挠度fe

剪力次弯矩挠度仅在孔洞处产生。

(1)孔洞1区

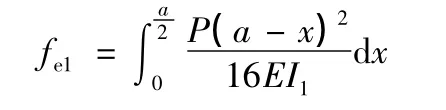
(2)孔洞2区

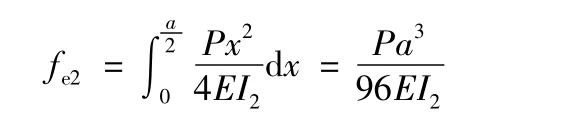
最终跨中挠度:

1.2 均布荷载作用下的跨中挠度

均布荷载作用下的跨中挠度的计算方法与前述跨中荷载作用下跨中挠度的计算方法完全一致，区别仅在于荷载函数上的不同。为避免重复累赘，在此就不列出。

2 理论公式简化

前面推导出的两端简支蜂窝梁在均布荷载和跨中集中荷载下的挠度计算式虽然在理论上严密，但是计算过于复杂，虽然采用VB编制程序，但仍不方便于工程应用。在此，通过所得VB程序进行大量实例计算，在此基础上利用统计规律建立基于扩张比、跨高比、截面尺寸等参数的简化计算式。

本文选择截面高度300～600 mm、扩张比1.3～1.7的8根钢蜂窝梁进行实例计算，梁编号从1号梁到8号梁，构件的跨高比逐渐降低，见表1。

表1 蜂窝梁算例截面尺寸(mm)

续表

2.1 集中荷载作用下跨中挠度计算式简化

2.1.1 弯矩挠度与当量挠度比值α1的简化

从计算结果看出，弯矩挠度与当量挠度的比值基本上随梁跨高比的变化幅度很小，可以认为跨高比对弯矩挠度的影响在满足工程精度的情况之下可以忽略不计。则影响弯矩挠度的因素为:(1)腹板抗弯系数β;(2)扩张比。

腹板抗弯系数β=腹板惯性矩/截面惯性矩

通过对计算结果进行曲线拟合，可得α1的简化计算式:

2.1.2 剪力挠度与当量挠度比值α2的简化

从计算结果可见，剪力挠度与当量挠度的比值α2随着梁跨高比的增大而减小。从理论上说，剪力挠度与梁跨度成线性关系，而弯矩挠度与梁跨度则成2次方的关系，可见计算结果与理论是相符合的。同时根据计算结果，得到每根梁的u－α2关系图，并进行曲线拟合。根据拟合曲线，1号～8号梁扩张比的变化对α2的影响不甚明显，将不同扩张比同截面的梁在不同跨高比下的剪力挠度与当量挠度比值α2与跨高比的关系拟合成一条曲线。

取3号梁为基本截面，定义待计算梁腹板面积为Aw，待计算梁单个翼缘面积为At，3号梁梁腹板面积为A'w，3号梁梁单个翼缘面积为A't，引入系数γ，

最后可得α2的计算式

2.1.3 次弯矩挠度与当量挠度比值α3的简化

由计算结果得知，当扩张比很小(如1.3)时，腹板削弱很少，次弯矩挠度与当量挠度比值α3最大也就1.7%。而随着扩张比的增大，开洞处T形截面不断削弱，次弯矩挠度与当量挠度比值α3增大得很快。当扩张比到1.7时，α3甚至超越α2达到62.8%。同时，随着跨高比的增大，剪力大小对跨中总挠度的影响逐渐减小，次弯矩挠度与当量挠度比值α3随着跨高比的增大而逐渐减小。

依然取3号梁作为基本截面，引入系数m

m=待计算梁截面惯性矩 /3号梁截面惯性矩 (8)得到α3的计算式:

最后可得集中荷载下两端简支钢蜂窝梁的跨中挠度计算式:

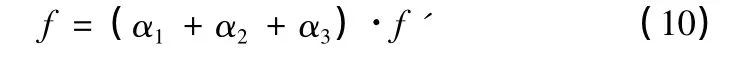
式中:f'为当量实腹梁跨中挠度。

2.2 均布荷载作用下跨中挠度计算式简化

2.2.1 弯矩挠度与当量挠度比值α1的简化

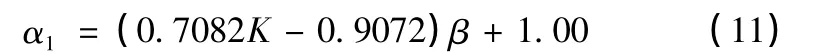
2.2.2 剪力挠度与当量挠度比值α2的简化

2.2.3 次弯矩挠度与当量挠度比值α3的简化

最后可得均布荷载下两端简支钢蜂窝梁的跨中挠度计算式:

3 ANSYS分析和公式校验

本文推得的均布荷载及跨中集中荷载作用下两端简支钢蜂窝梁挠度理论计算式和简化计算公式，为了校验该公式的准确性及精度，采用通用有限元分析软件ANSYS对梁1～8在不同扩张比时进行了有限元分析，一共取得数据80个，与VB程序所得结果(理论计算)、简化公式所得结果一并对比。

3.1 集中荷载作用下跨中挠度计算式简化

从计算结果看出，利用简化公式计算出来的蜂窝梁跨中挠度不太理想，与VB结果相比偏大，且比值随着梁跨度的增大也逐渐增大。经过对简化公式中α1、α2、α3的具体分析，发现经过曲线拟合之后α3值偏大，且对扩张比大小的反映过于强烈。在此，通过削弱跨高比的影响来达到减小α3值的目的，取

将α3值修正之后，根据修正之后跨中集中荷载作用下简化公式计算结果与ANSYS分析结果的比值，引入附加系数 λ1，令

则可得集中荷载作用下跨中挠度简化计算式:

3.2 均布荷载作用下跨中挠度计算式的简化

从对比结果可以看出，利用简化公式计算出来的蜂窝梁跨中挠度基本上都小于VB程序计算的结果，二者的比值在扩张比为1.5或1.6时最大，两端较小;二者的差值最大为8%，可见简化公式结果与VB程序结果还是基本符合的。

而有限元分析结果则全部大于简化公式计算结果，也大于VB程序计算结果。从理论上说，这是由于理论公式中并未考虑应力集中的因素，故这样的结果也是符合实际情况的。在此，需要对简化公式进行修正。

从简化公式计算结果与ANSYS分析结果的比值可以看出，该比值随着扩张比的增大而减小，这样，引入附加系数λ2，以此来反映扩张比对简化公式计算结果与ANSYS分析结果的比值的影响。经过反复试算，令

则可得

4 总结和展望

最后，通过前面得分析推导，得到以下成果:

(1)基于费氏空腹桁架分析法及三项挠度理论，推得两端简支钢蜂窝梁在均布荷载和跨中集中荷载的跨中挠度计算式，并将其编为BASIC程序。

(2)通过推出的理论计算式计算大量实例，在此基础上建立基于扩张比、跨高比、截面尺寸等参数的简化计算式，并利用有限元分析软件ANSYS对简化计算式进行修正。

本文由于条件所限，仅利用有限元分析软件ANSYS进行仿真分析，虽具有一定的参考价值，但还需要用实际的实验数据验证。同时，其他孔型如圆形孔和八角形孔等的蜂窝梁的跨中挠度研究本文并未涉及。

［1］何一民.蜂窝梁挠度的实用计算方法［J］.工业建筑，1994(8)

［2］苏益声.圆形孔与多边形孔蜂窝钢梁的试验分析［J］.广西大学学报(自然科学版)，2003(3)

［3］王洪范，王立新.蜂窝梁的应用和计算方法［J］.工业建筑，1994，24(8):3－4

［4］罗烈，罗晓霖.蜂窝梁设计规范的比较研究［J］.建筑钢结构进展［J］.2005，7(2)