中低地震活动地区的高层建筑钢筋混凝土梁柱的有限弹性设计
杨伯龙(译)
(中铁二院工程集团有限责任公司,四川成都610031)
1 介绍
高强度混凝土(HSC)的机械性能和反应与正常强度混凝土(NSC)不同。由于具有更高的强度-重量比率,故在高层建筑的梁柱建造中的使用尤为广泛。除了其更高的强度外,HSC同样有更大的初始弹性系数,剪力和抗张强度(Logan et al.,2009)。但是,一般情况下,HSC比 NSC更易裂。HSC更大的弹性系数导致了轴向压力中混凝土芯膨胀更小,这样就可以减少梁柱中侧向钢筋的约束性能(Mirmiran and shahawy,1997;Lu and Hsu,2007)。在属于屈曲和轴向压力的高强度混凝土钢筋(HSRC)梁柱中,情况更不如人意。试验(Li等,1991;Bayrak 和 Sheikh,1998;Paultre 等,2001;Ho和 Pam,2003a,2003b;Havaei等,2009;Zhou 等,2009)和理论(Wu 等,2004;Elmenshawi和 Brown,2009;Lam 等,2009a)显示,所使用的高强度混凝土的HSRC梁柱如果没能得到足够的约束,将极为脆弱。此外,用于HSRC梁柱的钢筋量应比普通强度的钢筋混凝土(NSRC)梁柱更多,这样才能保持其相同的延性(Lam等,2009b)。以上说明,HSRC梁柱的设计与NSRC不同。据此,我们需要基于性能设计对HSRC结构部件的设计进行全面的检查(Moehle,2006;Klemencic等,2007;Lew,2007;Englekirk,2008;Fry 等,2009;Goel等,2009;Yousuf和 Bagchi,2009)。
钢筋混凝土梁柱有限延性设计。对于位于地震危险区的建筑物来说,应该考虑HSRC结构的设计,以此作为释放由地震所产生的大量能量的有效方法。一般情况下,这通过安装减震器(Chung等,2009;Heo等,2009;Lee等,2009;Marano和 Greco,2009),采用基础隔震设计(Ribakov,2009;Takewaki和 Fujita,2009;Yamamoto 等,2009)或采用有效的钢筋结构,比如在指定位置形成塑性铰,即形成非弹性结构损坏释放多余能量,但不是通过塌陷释放多余能量(Park,2001)。较比与减震器的安装和基础隔震方法,钢筋混凝土的细节设计所需费用更少,并且适用于所有类型的结构。基于此方法,结构工程师应该计算在遭受地震时所形成的塑性铰的位置。塑性铰所在的结构构建应有足够的弯曲延性和/或形变性,从而在大型非弹性形变中释放能量。对属于带有或不带有轴向荷载曲度的钢筋混凝土来说,人们普遍认为通过在混凝土芯中增加围压,其弯曲延性和/或形变性可以得到显著的提高。围压的提升可以通过在密闭空间和/或以更大的直径安装横向钢筋(Park,1982;Li等,1991;Ho和Pam,2003a,2003b,Ho等,2009),例如使用圆形或方形的中空钢管来加固混凝土部件(Uy,1998;Ellobody和 Young,2006;Bambach等,2008),使用外部钢板(Kim 等,2008;Sabouri-Ghomi等,2008;Su等,2009)以及通过纤维钢筋聚合物来包裹混凝土部件(Hong等2008;Lam和Teng,2009;Wu和Wei,2009)。在这些方法中,第一种方法,即通过安装加固混凝土钢筋在高层建筑结构的实际建筑中是最简单有效的方法。
对于位于高地震危险区的HSRC框架结构来说,梁柱的设计通常为具有完全延展性(Watson和Park,1994;Bayrak和Sheikh,1998;Paultre等,2001)。这样一来,在地震时,关键部分就会有大量的加固钢筋以形成塑性铰(Pam和Ho,2009;Yan和Au,2009)。但是,在中低地震地区,结构的延性需求降低(Tsang等,2009),如果同样准备完全延性梁柱,就可能导致钢筋过多,并且增加建筑成本(Pam和Ho,2009;Lam等,2009b)。如此,在维持弯曲延性的中等水平的同时可以减少加固钢筋量。目前为止,对HSRC梁柱来说,对伸入到后顶点区域的有限延展梁柱的完全曲度-力矩曲线的分析甚少,并且对纵向钢筋的应力路径的效果分析也很少(Pam等,2001;Ho等,2003)。大部分的试验研究都用于完全延性梁柱的的分析(Park,1982;Li等,1991;Sheikh 等,1994;Watson 和 Park,1994:Bavrak 和 Sheikh,1998;Paultre等,2001;Bae和 Bayrak,2008)。但是,对于 HSRC有限延性的弹性后效的测试受到了限制。
本文所进行的基于非线性曲度-力矩分析的延伸性参数研究被用来对有限延性HSRC梁柱的弯曲延性性能进行研究。在分析中,我们所采取的是之前所建立的受约束和不受约束的混凝土的应力-应变曲线(Cusson和Paultre,1995),而在大曲率下的弹性后效阶段的HSRC梁柱的软化阶段,同样概括了钢筋的应力路径性质。从所获得的结果来看,理论公式用于连接钢筋混凝土的容积率和各种结构参数,比如总的核心断面率,纵向和加固钢筋的屈服力度,纵向钢筋的面积比,混凝土抗压强度和轴向压力荷载等级。为了验证所提议的公式的有效性,根据公式得出的包含固定钢筋的HSRC梁柱的弯曲延性性能在实验中得到了调查。我们对8个混凝土圆柱强度为50~96 MPa的梁柱进行了测试,这些梁柱都为不同的轴向压力荷载等级并且具有很大的反向循环非弹性位移偏移。从测试结果看,这些梁柱所达到的曲率延性因数为10,我们认为这在有限延性HSRC梁柱的设计是足够的(新西兰标准组织,2006)。
2 梁柱材料的压力应变特性
2.1 混凝土的应力应变曲线
在此研究中,我们选择了由Cusson和Paultre(1995)所创建的混凝土的应力应变曲线来分析非线性曲度与力矩。混凝土压力和相应的混凝土应变的比率为:

此处的fcc和fco分别为受约束和未受约束的混凝土的最大抗压强度。对应fco,和fle的轴向混凝土应力的εco是最有效的受限压力,其通过以下公式计算:

式中:ke是由Mander等(1988)定义的效率系数;fhcc是在fcc下的约束钢中的压力;Ash和s分别是横截面和约束钢中的空间;c是混凝土芯的周边尺寸。
整个约束混凝土压力(f)和应力(ε)的关系为:
上升段:

下降段:

Cusson和Paulture(1995)给出了r,k1和k2的值。在估算公式中fhcc的值的时候,需要一个迭代过程。作为开始,约束钢筋εhcc的应变为:

首先,约束钢实在混凝土压力达到最大的时候产生。fle,fcc,εcc和 εhcc能够分别通过式(3);式(1);式(2)和式(6)计算得出。如果εhcc比钢筋所产生的应变大,那么就会约束钢筋,并且 fhcc=fys。另外,εhcc用于重新计算 fle,fcc,εcc,和εhcc的新值,直到其在1%的范围内集合。
2.2 钢筋的应力-应变曲线
带有应变-加强部分的直线理想弹塑性用于非线性曲度与力矩的钢筋应力-压力分析,这类弹塑性在收力和张力上都对称。应力-压力曲线通过式(7)给出:

此处的fsu为最大力度;εsu是在fsu处的最大应力,并且P通过式(8)给出:

在此次分析中,建议采用fsu=1.15fy,εsh=0.02和εsu=0.11(Ho等,2005;Bai和Au,2009),这与表1中所列的实际测量值相当接近。

表1 梁柱样品中的钢筋混凝土的机械特性(MPa)
3 非线性曲度-力矩分析
3.1 分析的预测和方法
分析中有五个基本预测:(1)在弯曲后,截面仍然保持为平面;(2)混凝土的抗拉强度可以被忽略;(3)在混凝土和钢筋之间没有相对滑动;(4)混凝土芯加固而混凝土保护层未加固;(5)认为通过钢筋向混凝土芯所增加的围压在整个混凝土受压部位为持续的。这些预测都被普遍接受并由各个研究人员所采纳(Pam 等,2001;Ho 等,2003,2005,2009;Bai和 Au,2009;Lam等2009a,2009b)。梁柱部分的曲度-力矩通过使用从零逐渐增大的梁柱部分的力矩来分析。在规定的力矩下,混凝土和钢筋中的应力通过横截面和其相应的应力-应变曲线的剖面决定。接着,中性轴深度和阻力矩通过轴和力矩平衡条件进行相应的测量。在曲度足以使阻力矩增加到最大前,需要重复以上程序,接着将最大力矩减小到50%。
通过分析,我们观察到,中性轴深度最初为曲率减少(Ho等,2003),但是,在达到最大力矩后,在弹性后范围内的中性轴深度迅速增加,并且超过了一定点。这取决于梁柱中的轴荷载等级,高拉钢应力开始减少,导致应力逆转。应力逆转减少了钢的张应力,这样一来,高拉钢变得更不会依赖应力路径。钢的卸应力路径与初始弹性系数相同,直到其在零应力下达到残余塑性应力εp。

图1 梁柱截面及参数

图2 力矩-曲度曲线
3.2 梁柱的非线性力矩-曲度曲线
用作图1中的普通梁柱截面尺寸分析所选择的力矩-曲度曲线都在图2中。显然,最大力矩和后顶点分支都受到了混凝土强度,轴荷载等级和围钢比率的显著影响。从图2(a),2(b)可以看出,最大力矩随着混凝土强度轴荷载的增加而增加,超过了等级0.3的轴荷载强度,最大力矩开始降低。观察到梁柱的弯曲延性因混凝土强度和轴向荷载水平的增加而显著减少。相反,钢筋的增加总是能够增加弯曲延性。
4 弯曲延性分析
4.1 最大曲度延性因数
弯曲延性通过最大弯曲延性因数μc表示:

此处的φu和φy是极限并且是相应的降伏曲率(Watson和Park,2004)。极限曲度是当最大力矩(Mp)降到80%的时候所产生的力矩最大限度的曲度。当曲率从0.75Mp外推达到Mp时,采用降伏曲率。
4.2 参数研究
使用图1中的梁柱截面进行HSRC延性调查的广泛参数研究。混凝土的圆柱体压力(fc)从50 MPa到100 MPa不等。纵向钢筋百分比(ρ)从1%到6%不等,约束钢筋百分比(ρs)从1%到4%不等,核心区比率(Ag/Ac)从1.2到1.4不等,同时轴向荷载等级P/(Agf'c)从0.1到0.7不等。当横向钢是250 MPa或460 MPa时,纵向高屈服点钢强度为460 MPa。
4.3 分析结果
式(10)用于计算有限延性HSRC梁柱的钢箍配筋率。

式(10)中的细节设计的端部弯曲至少为 135°,以此在切点6d的最小延续长度上形成一个45°的钩度,其中d是横向钢的直径(图3)。在早期的试验研究中(Ho和Pam,2003b),关键区域中的135°钩应保持完整无缺,这样就能够产生有效的横向约束以延迟纵向钢筋的非弹性弯曲。但是,相同的研究同样显示了在梁柱关键区的90°钩状部分在更大的非弹性梁柱曲度下很容易开启。用于设计有限延性HSRC梁柱的公式的有效性将通过试验验证。

图3 带45度弯钩的箍筋的弯曲细节
5 试验项目
在结合轴向压力和循环非弹性位移偏移下,8个梁柱通过6 600 kN的自反力钢筋荷载框架测试。这些钢筋的圆柱体抗压强度从50 MPa到96 MPa不等,轴向压力等级从0.1到0.65不等,纵向钢筋配筋率从0.9%到6.1%不等,高屈服强度钢强度为339 MPa或531 MPa。通过水平刚性梁弯曲梁柱末端以让整个反向圆柱产生弯曲力矩和位移。图4反映了测试过程的样本。表1总结了钢筋混凝土的机械特征。表2总结了梁柱测试样品的细节。

表2 梁柱样品的界面特征
5.1 测试样本
图4显示了包含一个梁柱,水平横梁和一个上凸缘。梁柱的横截面尺寸为325 mm×325 mm,高度为1 515 mm。其代表了反向弯曲和最大弯曲力矩点之间的钢筋混凝土抗弯框架的实际存在的梁柱。反向弯曲和最大弯曲力矩点分别位于束柱结合点的中部和表面。纵向钢的面积比从0.9%到6.1%不等。关键区域的箍筋含量通过式(10)计算,而区域外的箍筋只用于抵抗最大剪力。应该注意的是,混凝土强度,轴向荷载等级和纵向以及箍筋的屈服强度的特定值(对于所有除了强度为250 MPa的NEW-80-01-09-S的箍筋外,所有纵向和箍筋的强度为460 MPa)都用于计算指定的箍钢比率,这在表2中以p's列出。为了测试的需要,关键区域的先决长度用于每个样本(Pam和Ho,2009),也就是说,对于高轴向荷载等级的梁柱,其长度为650 mm(比如,NEW-60-06-61-S,NEW-60-06-61-C 和 NEW-100-06-61-C);对于中等轴向荷载等级的梁柱,其长度为500 mm(比如,NEW-100-03-24-S,NEW-100-03-24-C,NEW-80-03-24-C 和 NEW-100-03-61-C);对于低轴向荷载等级的梁柱,其长度为325 mm(比如,NEW-80-01-09-S)。

图4 试体尺寸
水平刚性梁的设计在整个测试中都具有弹性,并且为产生最大力矩的梁柱的一端提供固定的支持。所设计的在梁柱另一端的凸缘足够强以抵挡屈曲和剪力,从而进行荷载框架铰链的连接。

图5 测试装置
5.2 监测仪器
纵向和横向钢上的压力测试仪分别用于测试弯曲和剪力以及局限应力。图5中显示了压力测试仪的位置。7对线性可变位移传感器(LVDTs)安装于图5中所示的梁柱测试样品的极限张力和受压纤维中。液压伺服用于维持最大梁柱曲率。在梁柱顶端安装了一个LVDT((±150 mm的冲程)以测量梁柱的旁向偏转。在每个MITS的液压伺服制动器中的测力传感器用于测量荷载。在液压制动器上所安装的一个外部荷载槽将轴向荷载加于梁柱。
5.3 测试程序
第一轮测试为荷载控制。其中,梁柱先后受到0.75Mu和-0.75Mu的荷载(正时针方向为正),同时,根据欧洲规范2(ESC,2004),Mu为理论梁柱绕曲强度。在梁柱顶部的横向位移分别记录为Δ1和Δ2,近似屈服位移为Δ3,由式(11)决定:

随后的测试为位移控制。在第二轮测试中,梁柱顶部的水平位移增加到了+Δy和-Δy,从而分别达到了μ=+1和-1。μ为近似位移延性系数,定义为

在式(12)中,Δ=所测量的梁柱顶部的水平位移。第三周期开始时,当μ=2,梁柱属于两个完整的周期。在每两个周期结束后,如果强度的降低不太大,那么μ就增加1。此过程重复直到测量力矩的能力小于最大测量屈曲量的80%。

图6 试验力矩位-位移滞后曲线
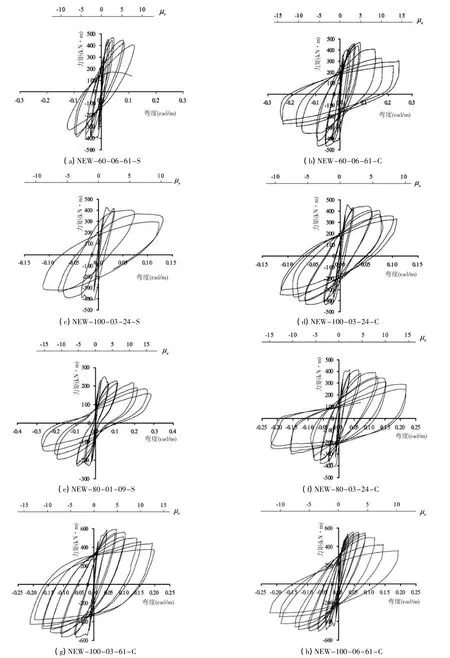
图7 试验力矩-弯度滞后曲线RC梁柱的有限延性
5.4 测试观察
在测试过程中,对于除了 NEW-80-01-09-S之外的所有的梁柱样品的第一次荷载控制弹性周期均未发现屈曲裂痕。当μ=±1时,第二轮中相应的张力纤维发生第一次屈曲张力裂缝。对于属于低轴向压缩荷载等级和少量的纵向钢的 NEW-80-01-09-S,当 μ=±0.75时,在第一周期中首先出现屈曲张力裂缝。同样,在除了NEW-80-01-S之外的所有梁柱中,当梁柱顶部的水平位移接近μ=±2的时候,外缘上方的混凝土出现散裂。但是对于NEW-80-01-09-S,当μ=±3的时候,混凝土的上方散裂。由于在不断的弹性周期内,水平位移不断增加,混凝土顶部继续散裂,最终,由于混凝土盖的散裂,纵向钢弯曲而破坏。
测试梁柱的混凝土顶盖散裂和纵向钢弯曲的第一个可见标志如图6所示,表现在其分别的实验性的力矩位移滞后曲线。
6 测试结果
6.1 力矩位移和力矩弯度滞后曲线
梁柱样本的力矩位移和力矩弯度滞后曲线都分别在图6和图7中显示。理论力矩量基于欧洲规范2(ECS2004)计算,Mu在图6中为水平实线,这条线上的点和虚线表示了因P-Δ效果的第二力矩。同样在图6中的为近似(μ)和实际(μ)位移延性因数的量。
按照图6中所展示的滞后曲线,我们可以观察到:
(1)梁柱的最大力矩量总是发生在非弹性范围内。属于最大轴荷载等级的梁柱,比如 NEW-60-06-61-S,NEW-60-06-61-C 和NEW-100-06-61-C,在 μ=±3或±4 的第一个周期内获得最大正反力矩。所有其他属于中等或小的轴荷载等级的梁柱,在周期为μ=±2或±3时达到其弯曲强度。在高于弹性周期所发生的最大力矩量主要由于在弹性后效范围内发生的围加固的约束效应(Pam和Ho,2002);

(2)对于属于高轴荷载等级的HSRC梁柱,比如NEW-60-06-61-S,NEW-60-06-61-C 和 NEW-100-06-61-C,围加固量导致其有适度的延性,当其最终达到至少μ=±5(偏移=±5);
(3)结果显示围加固的适当的量,通过式(10)来计算,能够防止HSRC在达96 MPa的混凝土圆柱强度的时候碎裂或突然断裂。
从图7可以看出,梁柱弯度在两个周期后迅速增加,其原因为:(1)由于非弹性行为而导致的梁柱中累积的大部分残留应变;(2)弯曲裂缝的形成;(3)混凝土盖的延展散裂;(4)纵向钢的非弹性屈曲;(5)关键区的形成。同样,在所有损坏发生之前,所有梁柱的样本都达到了μc≈10。梁柱样本的有限延性通过足够的围加固达到,这根据梁柱关键区的式(10)计算。
6.2 力矩-弯度曲线包络线
图8对测量和理论的力矩-弯度曲线的包络线进行了对比。理论曲线通常以积极的方向考虑,同时基于实际材料强度得出。图中明确显示的是分析力矩-弯度曲线几乎与上升段的试验曲线相一致。但总的来说分析曲线在很小的程度上对梁柱样本的后顶点力矩-曲线估计不足。
6.3 位移和曲度延性因数
位移和弯度延性因数用于实验性研究以对HSRC梁柱的弯度延性进行评估。位移延性因数是指由部件的材料强度,轴荷载等级,长度和几何尺寸所决定的部件完整延性。另外,弯曲延性因数指的是部件延性,这取决于部件几何尺寸,材料强度和轴荷载等级。

图8 理论和试验力矩-曲度曲线
位移延性因数有两种。第一种为近似位移延性因数(μ),此因数的计算是基于理论弯度强度(Mu)得到的实验性的横向位移得出。第二个定义是基于所测量的弯曲强度,由于Mp>Mu,这就被称为实际位移延性因数(μ')。实际屈曲位移和实际位移延性因数能够分别表达为:

Δ1'和Δ2'分别是在0.75Mp所测量的横向位移。
为了测量梁柱的弯曲延性,极限实际位移延性因数(μd)和极限弯度延性因数(μc)都在此研究中采用。两个延性因数分别说明了当Mp的弯曲强度减少20%的时候,在梁柱顶部和最大梁柱弯度处的水平位移程度。μc的值能够通过式(9)计算得出,而μd可通过式(15)算得:

此处的Δu是极限位移,这是当力矩在后顶点范围内达到0.8Mp的时候测量所得。
μd和μc的值与其相应的塑变值都列于表3中。我们可以看到的是对于所有梁柱样本的μc的值都接近10,这可以作为有限延性的测量值。这样的设计对位于中低地震危险区的高层建筑的HSRC来说是合适的,可以防止完全延性反应的发展。

表3 极限实际位移和弯度延性因数
7 结论
在弹性后效区域中的非线性力矩-曲度曲线经过了分析和试验的研究,以此来调查有限延性HSRC梁柱的弯曲延性性能。分析是以基于混凝土和钢筋的应力-压力为基础,这些应力-压力与弹性后效范围的张力钢筋的应力路径的依赖效果相配合。通过对比理论力矩-曲度曲线和试验基本框架,我们可以看到理论曲线几乎与试验框架相一致,除了一些后顶点范围内的估计不足。结果是,使用非线性力矩-曲线分析来进行综合参数研究,从而将围加固的容积比与各种参数相联系,以用于HSRC梁柱的有限延性的设计。
根据所提出的公式设计的包括围加固在内的HSRC梁柱的弯曲延性通过试验进行了研究。应力为50~96 MPa的8个混凝土HSRC梁柱通过0.1~0.65的各种等级的轴向压力荷载和反向圆柱非弹性位移突出计算并测试。测试结果很明显的显示了所有梁柱样本的最大弯曲延性因数都接近10,这可以当作有限延性的标准。这样的设计适合在中低地震危险区的高层建筑的HSRC梁柱中,而完全延性梁柱的设计太多余,并且不是必须的。
[1]Bae S,Bayrak O.钢筋混凝土的塑性铰链长度[J].ACI结构期刊,2008,105(3):290-300
[2]Bambach M R,Jama H,Zhao X L,Grzebieta R H.横向冲击负载下的中空和混凝土钢筋的中空部分[J].工程结构,2008,30:2859-2870
[3]Bai ZZ,Au FTK.混凝土梁柱的弯曲强度和延性的加固硬化效果[J].高层和特殊建筑的结构设计,2009.DOI:10.1002/ta.554
[4]Bayrak O,Sheikh SA.延性HSC梁柱的围加固设计[J].结构工程杂志,ASCE,1998,124(9):999-1010
[5]Chung H S,Moon B W,Lee S K,Park J H,Min K W.使用 RC 剪力墙系统的摩擦阻尼器的抗震性能[J].高层和特殊建筑物的结构设计,2009,18:807-822
[6]Cusson D,Paultre P.加围高强度混凝土的应力-压力模式[J].结构工程杂志,1995.ASCE121(3):468-477
[7]Ellobody E,Young B.混凝土冷凝不锈钢钢管梁柱的设计和性能[J].工程结构,2006,28:716-728
[8]Elmenshawi A,Brown T.通过超高强度混凝土修建属于周期荷载的R/C构件的模型标准[J].高层和特殊建筑的结构设计,2009.DOI:10.1002/tal.532
[9]Englekirk RE.抗震设计程序的需求[J].高层和特殊建筑物的结构设计2008,17:1005-1013
[10]欧洲标准化委员会(ECS).2004.欧洲规范2:混凝土结构设计:1-1部分:建筑的普通规则和规则[S].英国标准机构:伦敦,UK:225
[11]Fry J A,Hooper J D,Klemencic R.太平洋地震工程研究/加利福利亚地震安全委员会的隔心墙方案研究[J].高层和特殊建筑物,2009.DOI:10.1002/tal:544
[12]Goel S C,Liao W C,Bayat M R,Chao S H.用于抗地震结构的基于效能的塑性论设计(PBPD)方法:概观[J].高层和特殊建筑物2010,9(1-2):115-137
[13]Havaei G R,Keramati A.在偏心荷载下的高层建筑的常规和交叉螺旋循环加固梁柱的强度和延性的试验和数据评估[J].高层和特殊建筑的结构设计,2009,DOI:10.1002/tal.534
[14]Heo J S,Lee S K,Park E,Lee S H,Min K W,Kim H,Jo J,Cho B H.用于减少建筑物结构双向反应的调整液体减震器[J].高层和特殊建筑物结构设计,2009(18):789-805
[15]Ho J C M,Au F T K,Kwan A K H.混凝土梁的弯曲强度和延性的钢加固机械硬化的效果[J].结构工程和机械,2005,19(2):185-198
[16]Ho J C M,Lam J Y K,Kwan A K H.高强度混凝土梁柱加固和增强延性的有效性[J].工程结构2010,32:714-725
[17]Ho J C M,Pam H J.高强度加固混凝土梁柱的弹性后反应的横向钢结构[J].香港工程机构交易2003,10(2):1-9
[18]Ho J C M,Pam HJ.地轴向荷载高强度加固混凝土梁柱的非弹性设计[J].工程结构2003,25(8):1083-1096
[19]Ho J C M,Kwan A K H,Pam H J.普通和高强度混凝土横梁的后顶点弯曲结构的理论分析[J].高层和特殊建筑物的机构设计,2003,12(2):109-125
[20]Hong W K,Park S C,Kim H C,Kim J M,Kim S I,Lee S G.通过GFRP渠道和CFRP半片加强的加固混凝土梁柱的试验性研究[J].高层和特殊建筑物的结构设计,2009
[21]Kim S B,Lee Y H,Scanlon A.高层住宅楼的结构材料质量的对比研究[J].高层和特殊建筑物的结构设计,2008,17:217-229
[22]Klemencic R,Fry J A,Hooper J D,Morgen B G.延性混凝土隔心墙建筑基于性能的设计-在细节分析之前考虑的问题[J].高层和特殊建筑物的结构设计2007,16:599-614
[23]Lam J Y K,Ho J C M,Kwan A K H.具有最小加固的高强度混凝土梁柱的弯度延性.材料和结构2009,42(7):909-921
[24]Lam J Y K,Ho J C M,Kwan A K H.混凝土梁柱的有限延性设计的最小轴向荷载等级和最小加固[J].计算机和混凝土2009,6(5):357-376
[25]Lam L,Teng J G.在循环轴向压力上用于FRP-侧限混凝土应力-压力[J].工程结构,2009,31:308-321
[26]Lee S K,Lee.S Y,Min K W,Moon B W,Youn K J,Hwang J S.考虑到泥土结构的交互作用,对建筑物结构内的MR减震器进行性能的评估[J].高层和特殊建筑结构设计2009,18:105-115
[27]Lew M.2Li B,Park R,Tanaka H.高地震区的高层建筑的设计[J].高层和特殊建筑的结构设计1991,16:537-541
[28]Li B,Park R,Tanaka H.在地震荷载下的高强度混凝土梁柱结构的加固效果[C]∥奥克兰:地震工程太平洋会议记录,1991:20-23,67-68
[29]Logan A,Choi W,Mirmiran A,Rizkalla S,Zia P.高强度混凝土的短期机械特质[J].ACI材料杂志,2009,106(5):413-418
[30]Lu X,Hsu C T T.三轴压力下的高强度混凝土切线泊松比[J].混凝土研究杂志,2007,59(1):69-77
[31]Mander J B,Priestley M J N,Park R.用于加固混凝土的理论应力-压力模型[J].结构工程杂志,ASCE1988,114(8):1804-1825
[32]Marano G C,Greco R.在中级地震下的高层建筑的调整质量减震器的耐用的最佳设计[J].高层和特殊建筑的结构设计,2009,18:823-838
[33]Mirmiran A,Shahawy M.侧限混凝土的膨胀特征[J].凝聚力和摩擦材料的机械,1997,2:237-249
[34]Moehle JP.地震研究、高层建筑的设计和检查[J].高层和特殊建筑物的结构设计,2006,15:495-513
[35]Pam HJ,Ho J C M.加固混凝土梁柱的弯曲强度增强[J].土木工程机构,结构和建筑物,2001,146(4):363-370
[36]Pam H J,Ho J C M.有限延性高强度混凝土梁柱中的箍钢关键区的长度[J].工程结构,2009,31:2896-2908
[37]Pam H J,Kwan A K H,Ho J C M.加倍增强的正常和高强度混凝土梁柱的后顶点结构和弯曲延性[J].结构工程和机械,2001,12(5):459-474
[38]Park R.方形侧限混凝土梁柱的延性[J].结构工程杂志,ASCE1982,108(2):920-950
[39]Park R.增加地震中结构的抵抗力[J].新西兰国家地震工程社会公报,2001,34(1):1-39
[40]Paultre P,Legeron F,Mongeau D.混凝土强度和横向箍筋屈服强度对高强度混凝土梁柱结构的影响[J].ACI结构杂志2001,98(4):490-501
[41]Ribakov Y.带有选择性控制半活动摩擦减震器的基础隔震结构[J/OL].高 层 和 特 殊 建 筑 结 构.http://dx.doi.org/10.1002/tal.527
[42]Sabouri-Ghomi S,Kharrazi M H K,Mam-Azizi S D,Sajadi R A.钢板剪力墙系统压曲[J].高层和特殊建筑物的结构设计2008,17:823-837
[43]Sheikh S A,Shah D V,Khoury S S.高强度混凝土梁柱的侧限。ACI结构杂志,1994,91(1):100-111
[44]新西兰标准组织,NZS3101,2006.混凝土结构标准,第1部分-混凝土结构的设计[S].新西兰,惠灵顿
[45]Su R K L,Lam W Y,Pam H J.钢板加固复合材料深梁实验性研究[J].高层和特殊建筑结构设计,2009,18:235-257
[46]Takewaki I,Fujita K.高层和基础隔震建筑中及时的地震能量输入和频繁的双重领域[J].高层和特殊建筑物的结构设计,2009,18:589-606
[47]Tsang H H,Su R K L,Lam N T K,Lo S H.现有建筑结构中的抗震需求的快速评估[J].高层和特殊建筑的结构设计,2009,18:427-439
[48]Uy B.所有高层建筑的延性,强度和混凝土钢箱柱[J].高层和特殊建筑的结构设计,1998,7:113-133
[49]Watson S,Park R.钢筋混凝土梁柱的模拟地震荷载测试[J].结构工程杂志,ASCE1994,120(6):1825-1849
[50]Wu Y F,Oehlers D J,Griffi th M C.RC梁柱截面的弯曲形变量的有效定义[J].工程结构,2004.26:641-650
[51]Wu Y F,Wei Y Y.CFRP-侧限方形混凝土梁柱强度比率的横截面方面的效率[J].工程结构,2010,32:32-45
[52]Yamamoto K,Fujita K,Takewaki I.地震隔离建筑的不断的地震输入能量和敏感度[J].高层和特殊建筑的结构设计,2009
[53]Yan Z H,Au F T K.20层加拿大钢框架建筑的抗震性能[J].高层和特殊建筑的结构设计,2009
[54]Zhou Y,Lu X,Lu W,Oian J.多塔楼连接结构的抗震性能研究[J].高层和特殊建筑结构设计,2009
注释
Ac围加固外所测量的核心混凝土区
Ag截面积的总共混凝土
Ash围加固截面面积
C 混凝土核心区边尺寸
d 围加固的直径
Eg钢筋弹性系数
f 混凝土压力
fc混凝土圆柱体强度
fcc,fco限制或非限制混凝土压力强度
fhcc在最大限制混凝土压力下的箍钢压力
fle有效侧面加围压力
fs钢筋压力
fsu钢筋的极限强度
fy纵向加固的屈服强度
fys围加固的屈服强度
ke约束有效性系数
Mp所测量的最大力矩量
Mu梁柱的理论弯曲强度
P 压力轴荷载
P 钢筋应力-压力曲线的压力硬化部分的参数(Eq.8)
R 具体屈曲强度为250兆的高屈曲形变钢筋
s 围加固的中心-中心空间
T 具体屈曲强度为460兆帕的高屈曲形变钢筋
Δ 梁柱顶部所测量的水平位移
Δu后定点在0.8Mp的梁柱顶部所测量的水平位移
Δy,Δy' 近似和实际屈曲位移
Δ1,Δ2 在+0.75Mu和-0.75Mu处的梁柱水平位移
Δ1',Δ2' 在+0.75Mp和-0.75Mp的梁柱水平位移
ε 混凝土压力
εcc,εco在受限和非受限混凝土顶部压力的混凝土应力.,
εhcc在混凝土顶部压力上的箍钢应力
εp在应力反转后的零压力钢筋的残留塑性应力
εs钢筋应力
εsh应力硬化开始时的钢筋应力
εsu极限钢筋应力
εy钢筋屈曲应力
φu,φy极限和屈曲弯度
μ,μ' 近似和实际位移延性因数
μc极限弯曲延性因数
μd极限实际位移延性因数
ρ 纵向钢面积率
ρs梁柱样本中箍钢的实际容积率
ρs' 通过Eq.(10)计算的箍筋的配筋率
缩写
HSC 高强度混凝土
HSRC 高强度加固混凝土
LVDT 线性变量位移传感器
NSC 正常强度混凝土
NSRC 正常强度加固混凝土
NZS 新西兰标准组织
RC 钢筋混凝土

