基于蚁群优化支持向量机模型的公路客运量预测

孙 煦， 陆化普， 吴 娟，2

（1.清华大学 交通研究所，北京 100084；2.军事交通学院 汽车指挥系，天津 300161）

0 引 言

随着社会经济的持续快速发展，人们的出行也更加频繁，公路交通运输得到了飞速的发展。其中，客运量是衡量公路运输发展程度的重要指标，可以反映社会经济发展现状和人民生活水平，而科学准确地预测公路客运量及其发展的趋势、特点和规律，是制定公路客运发展规划以及规划公路客运站场的重要理论依据［1］。国内外对公路客运量预测方法的研究经历了一个很长的阶段，早期主要是以时间序列法、弹性系数法、回归分析法、灰色系统预测法等传统方法为代表［2］，而这些传统方法主要是集中在对数据本身规律的回归和时间趋势外推的分析上，对客运量生成与影响因素的内在作用机理分析不够，使得数据隐含信息量丢失较大。近年来，人工神经网络被广泛应用于客运量预测中，它具有识别复杂非线性系统的特性，但是也存在着收敛速度慢、过学习和局部极值等问题［3］，这些问题都影响了其预测精度。

支持向量机（Support Vector Machine，简称SVM）是一种在统计学习理论基础上形成的、以实现结构风险最小化为原则的学习方法［4］。与人工神经网络相比，它克服了神经网络所固有的局部极小点、过学习现象以及结构和类型的选择过于依赖经验等缺陷。由于其具有模型的自由选择（参数、基函数的位置等）、全局最优以及良好的泛化能力等特性，因此在小样本、高维、非线性预测领域具有很好的应用效果［5］。但是和其他学习算法一样，支持向量机的性能依赖于学习机的参数，即训练参数的选择对支持向量机的预测效果有着较大的影响。因此，根据实际的数据模型选择合适的训练参数成为关键问题。

本文将蚁群算法与支持向量机结合，提出了基于蚁群的支持向量机参数优选方法，利用蚁群算法优化其训练参数，得到了优化的基于蚁群的支持向量机的公路客运量预测模型。以北京市1978—2009年公路客运量数据作为实验数据［6］，实验结果表明，相比于BP神经网络和传统的SVM方法，基于蚁群的支持向量机模型的预测精度更高、误差更小，可以更有效地对公路客运量进行预测。

1 支持向量机的基本原理

支持向量机是建立在统计学习理论和结构风险最小化原则基础上的机器学习方法。它能够根据有限样本信息，在模型复杂性和学习能力之间寻求最佳折衷［7］，有效地实现对基于小样本的高维非线性系统精确拟合，同时也避免了人工神经网络等方法存在的陷入局部最优解的问题，因此具有较好的推广性。

支持向量机理论可用于分类问题和回归问题，公路客运量的预测问题属于支持向量机的回归问题。其基本原理是：假设给定的训练样本为（xi，yi）（xi∈Rn为出入变量，yi∈Rn为对应输出值，i＝1，2，…，l），通过一个非线性映射φ将数据映射到高维特征空间F，从而将非线性回归问题转化为高维特征空间的线性问题，即

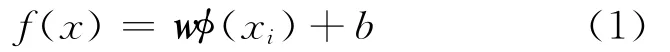
其中，φ（x）是将样本点映射到高维空间的非线性变换；w为权值矢量；b为阈值。

根据结构风险最小化原则，上述函数回归问题就是寻求使风险最小函数最小的f，即

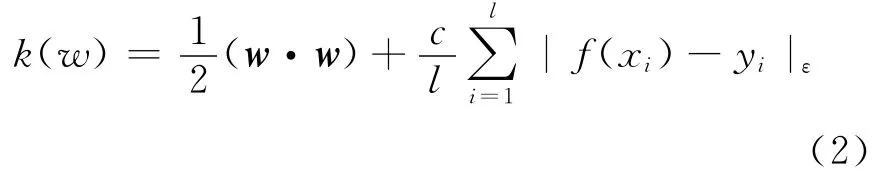
其中，等式右边前一项（w·w）表示函数f（x）的复杂性；后一项表示训练集上的平均损失；惩罚参数c则体现了函数的复杂性和训练集上平均损失之间的折中关系；ε为引入的不敏感损失函数，其定义为：

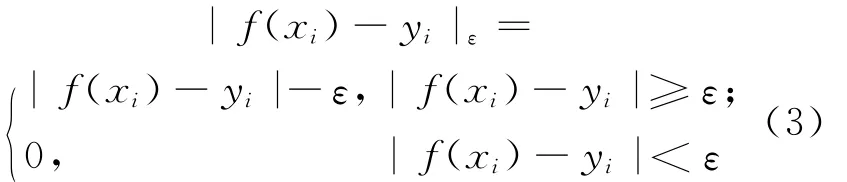
最小化（2）式引入非负松弛变量ξi和（i＝l，2，…，l），转化为等价最优化问题：

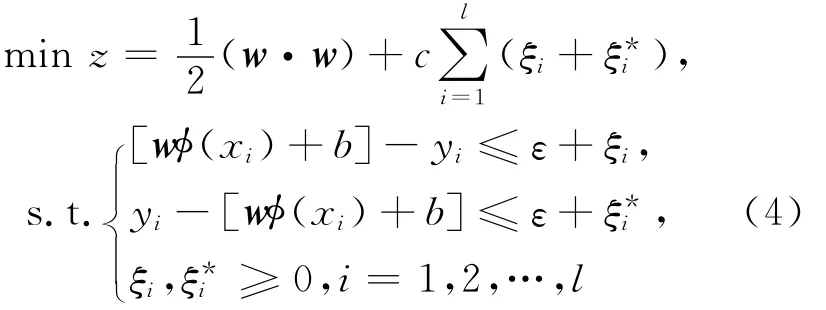
引入Lagrange乘子αi及，上述优化问题转化为对偶问题：

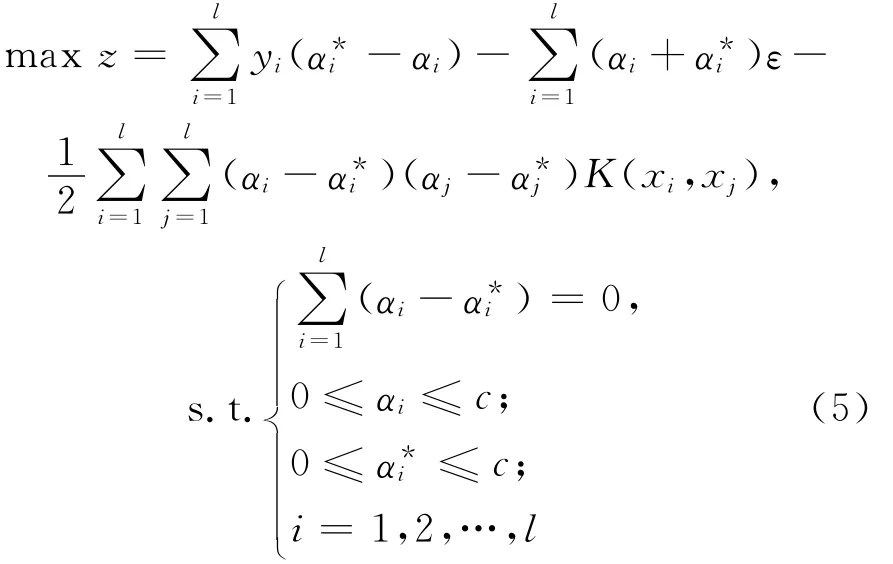
其中，当αi－非零时对应的训练样本为支持向量；K（xi，xj）＝φ（xi）·φ（xj）为核函数，其作用是不必知道从低维输入空间到高维特征空间非线性映射φ（x）的具体形式，通过引入核函数就可得到决策回归方程［8］。常用的非线性核函数有径向基核函数、多项式核函数等。鉴于径向基核函数构造的SVM具有较强的非线性预测能力，因而本文选择径向基核函数构造支持向量机。

从而得到回归函数：

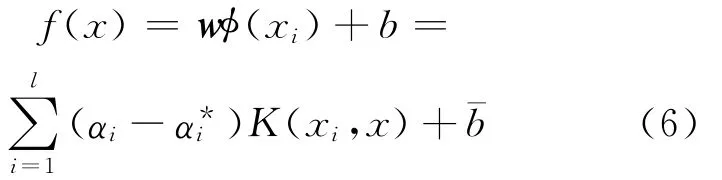
研究表明，支持向量机的预测精度很大程度上受到参数取值的影响［9］。而传统的参数选取基本都是根据经验反复试验来选取，选取的时间较长且结果的最优性无法保证。为了提高参数的选取速度和最优性，需要采用合适的智能优化算法在一定的区域内搜索各参数的最优组合，从而获得具有较强预测性能的支持向量机。

2 基于蚁群算法的SVM参数优化模型

蚁群算法是文献［10］通过模拟蚁群的觅食行为提出的一种新型模拟进化算法。它运用了正反馈、分布式计算和贪婪式启发式搜索。该算法适应性强，不用计算目标函数偏导数，搜索效率高，寻优能力突出，克服了其他智能算法容易陷入局部最优的缺点。

鉴于以上优点，本文采用蚁群算法建立支持向量机的参数选择模型，进行参数的优选。具体来说，就是将SVM的参数选取看作参数的组合优化，对组合优化问题建立目标函数，采用蚁群优化算法来搜索最优的目标函数值，从而找到合适的参数取值。该模型无需计算梯度等信息，且有较高的全局寻优效率。优化的流程如图1所示。

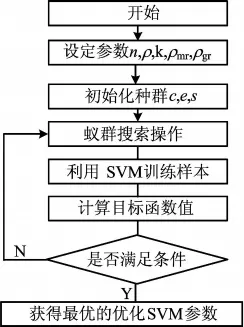
图1 基于蚁群算法的支持向量机参数优化流程图

基于蚁群算法的SVM参数优选过程中，由于目标函数中隐含了各蚂蚁所走过的所有节点的信息以及所建模型当前的准确度，因此蚁群系统是根据目标函数值来更新信息素的浓度从而进行反复的搜索寻优，所以目标函数的选择和蚁群搜索操作的实现是进行参数优选的2个重要步骤。

2.1 目标函数的选择

对于支持向量机回归问题，目的是要逼近系统的非线性模型［11］，因此以均方误差EMS来描述支持向量机回归与参考模型间的偏差，即

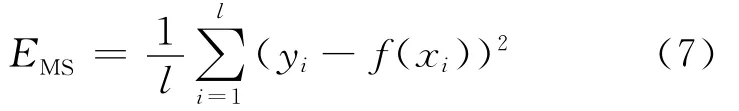
其中，l为样本个数；yi为参考模型的实际值；f（xi）为支持向量机计算的预测值。由此得到蚁群支持向量机模型的目标函数为：

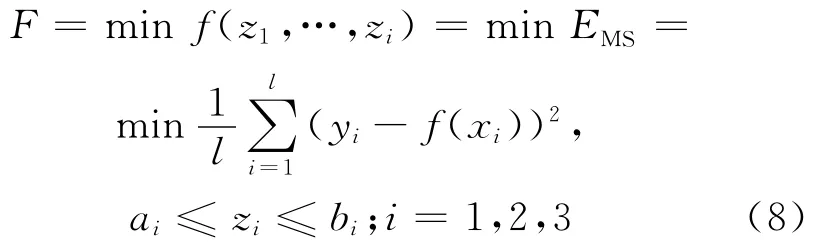
其中，优化变量zi总共为3个，对应于参数c、σ、ε；［ai，bi］为各个变量zi的定义域；yi为实际值；f（xi）为通过SVM计算出的预测值。目标函数即是选取最佳的参数组合，使得训练样本集的总误差最小，而寻参过程就是最小化F。

2.2 蚁群搜索操作步骤

2.2.1 相关参数的初始化设定

初始化确定蚁群算法的基本参数，如种群大小m、信息素更新比例因子ρ、信息素启发因子α等；确定蚁群搜索操作的终止条件（本文设定最大循环次数Nmax作为终止条件）。

2.2.2 节点及路径的生成

分别设定c、σ和ε具有相应的有效数位使得待优化变量X（统一代表这3个变量）具有n维分量，即X＝｛x1，x2，…，xn｝，同时将各分量等分成N个节点，并在xOy平面上表示出N＊n个节点，用符号 Knot（xi，yi，j）表示一个节点。xi（i＝1～n）中的N个节点组成一个层Li，共有n层。

设定蚂蚁数m，给每只蚂蚁k（k＝1～m）各定义一个具有n个元素的一维数组Pathk，在Pathk中依次存放第k只蚂蚁从L1层开始直至到达Ln层所要经过的n个节点的纵坐标值，可用来表示第k只蚂蚁的爬行路径。

2.2.3 迭代搜索

（1）设定初始时刻t＝0，m只蚂蚁都位于起始点处，搜索开始后，根据（9）式计算每只蚂蚁k（k＝1～m）从Li－1层向Li层的转移概率Pk（xi，yi，j），采 用 赌 轮 法 选 择 Li层 上 的 某 个 节 点Knot（xi，yi，j），从而转移到该节点，同时将该节点的纵坐标值存入Pathk的第i个元素中。t时刻的转移概率Pk（xi，yi，j）计算公式为：

其中，τ（xi，yi，j，t）为t时刻节点 Knot（xi，yi，j）上遗留的信息量，假设初始时刻各节点上的信息素相等，信息素增量为零，即τ（xi，yi，j，0）＝γ（γ 为常数），Δτ（xi，yi，j，t）＝0；η 表 示 由 Knot（xi－1，yi，j）到 Knot（xi，yi，j）的期望程度，与上一次循环的目标函数值F有关。

（2）经过n个时间单位后，m只蚂蚁都从起始点爬到终点，将蚂蚁k（k＝1～m）所走过的路径即数组Pathk组成一个解X＊，计算出相应的目标函数值F＊，比较各目标函数值，确定本次循环中的最优路径（即对应的目标函数值最小的路径），并记录与其对应的c、σ和ε值。

（3）令t＝t＋n，N＝N＋1，按照（10）式更新此时刻各节点上的信息量，并将Pathk（k＝1～m）中的所有元素清零。

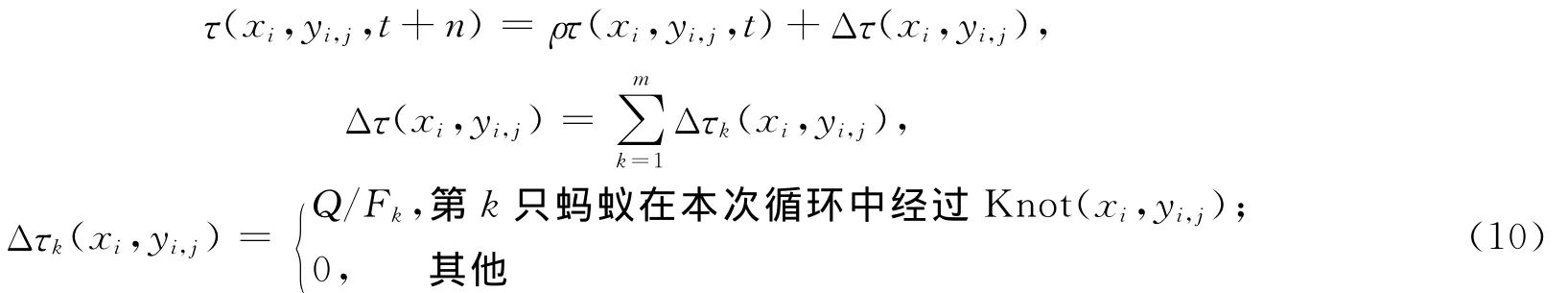
其中，Q为信息强度，它在一定程度上影响算法的收敛速度；Fk为第k只蚂蚁在本次循环中的目标函数值，由（8）式计算。

2.2.4 终止准则

本文的终止条件为预设的最大迭代次数Nmax。若N＜Nmax，且整个蚁群尚未收敛到走同一条路径，则再次将全部蚂蚁置于起始点0并重复操作迭代搜索中的各步骤，直到所有蚂蚁全部收敛到一条路；若N＜Nmax，且整个蚁群已收敛到走同一条路径，则算法结束，输出最优路径所对应的相应的c、σ和ε。

3 公路客运量预测实例分析

3.1 公路客运量预测

以北京市1978—2009年的公路客运量数据为应用实例（2006、2007年的数据由于具有特异性，因此剔除掉）。先以其中奇数年的公路客运量数据作为训练数据，形成训练样本集，以偶数年的数据作为测试数据，形成测试集；再以偶数年的公路客运量数据作为训练数据，形成训练集，以奇数年的数据作为测试数据，形成测试集，从而对模型进行反复训练。模型的各参数设置如下：c的取值范围为（0.01，200），ε的取值范围为（0，0.8），σ的取值范围为（0.001，100）；蚂蚁种群大小m＝50，最大迭代 Nmax＝500，信息素更新比例因子ρ＝0.7，α＝1，β＝5，Q＝100。

3.2 预测结果分析

数据的归一化结果见表1所列。为了验证模型的有效性，同时选取了BP神经网络法及使用交叉验证试算的传统SVM法对同一实例进行预测。选取以下2个误差指标作为各种方法预测效果判断的依据（yi指样本提供的实际值，yi＊指根据模型求得的预测值，n为预测值个数），即相对误差ERP和平均绝对百分比误差EMAP。

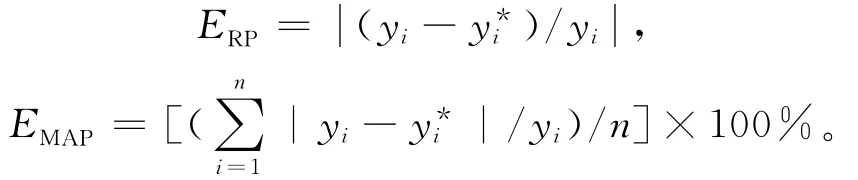
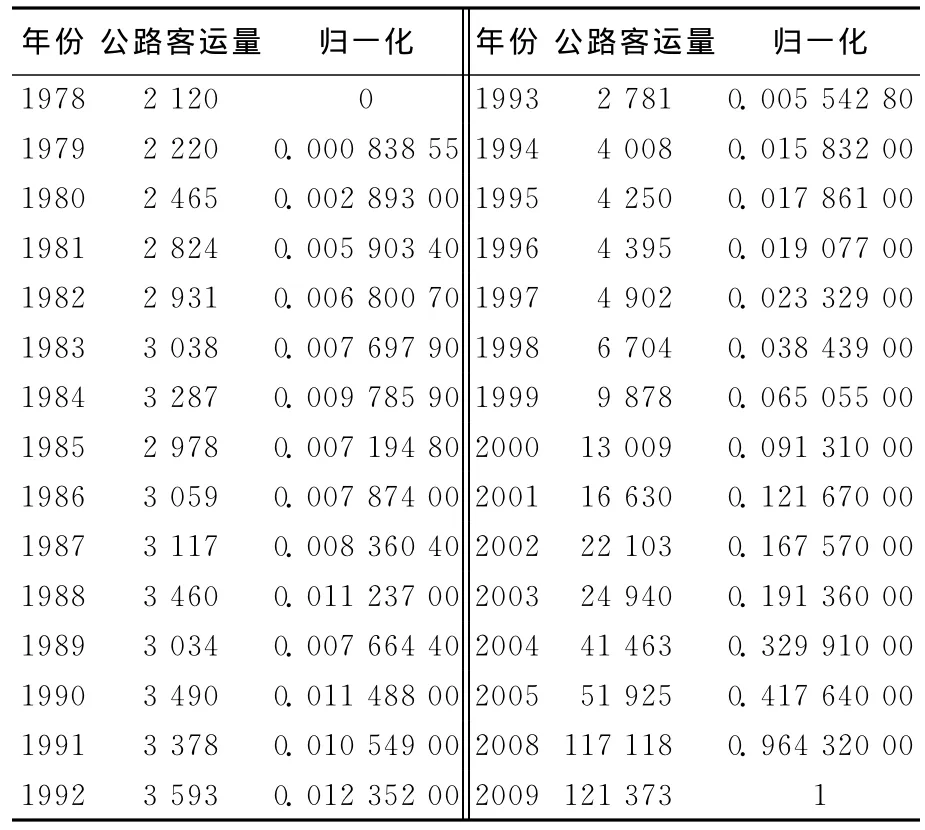
表1 数据及归一化结果 104人

通过对训练样本集进行反复训练［12］，选择最优的模型参数，从而分别建立蚁群支持向量机预测模型、BP神经网络预测模型以及传统SVM预测模型。

利用3种模型通过训练奇数年份的数据所得到的偶数年份客运量的预测结果对比如图2所示，利用3种模型通过训练偶数年份的数据所得到的奇数年份客运量的预测结果对比如图3所示。

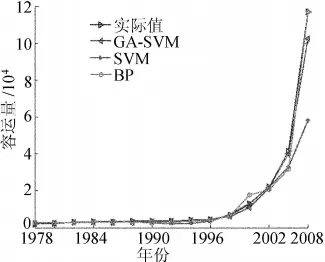
图2 偶数年份客运量数据预测结果比较

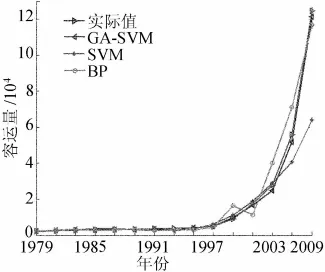
图3 奇数年份客运量数据预测结果比较

3种方法在2次预测中得到的所有年份的预测值以及与实际值相比较得到的误差结果见表2所列。

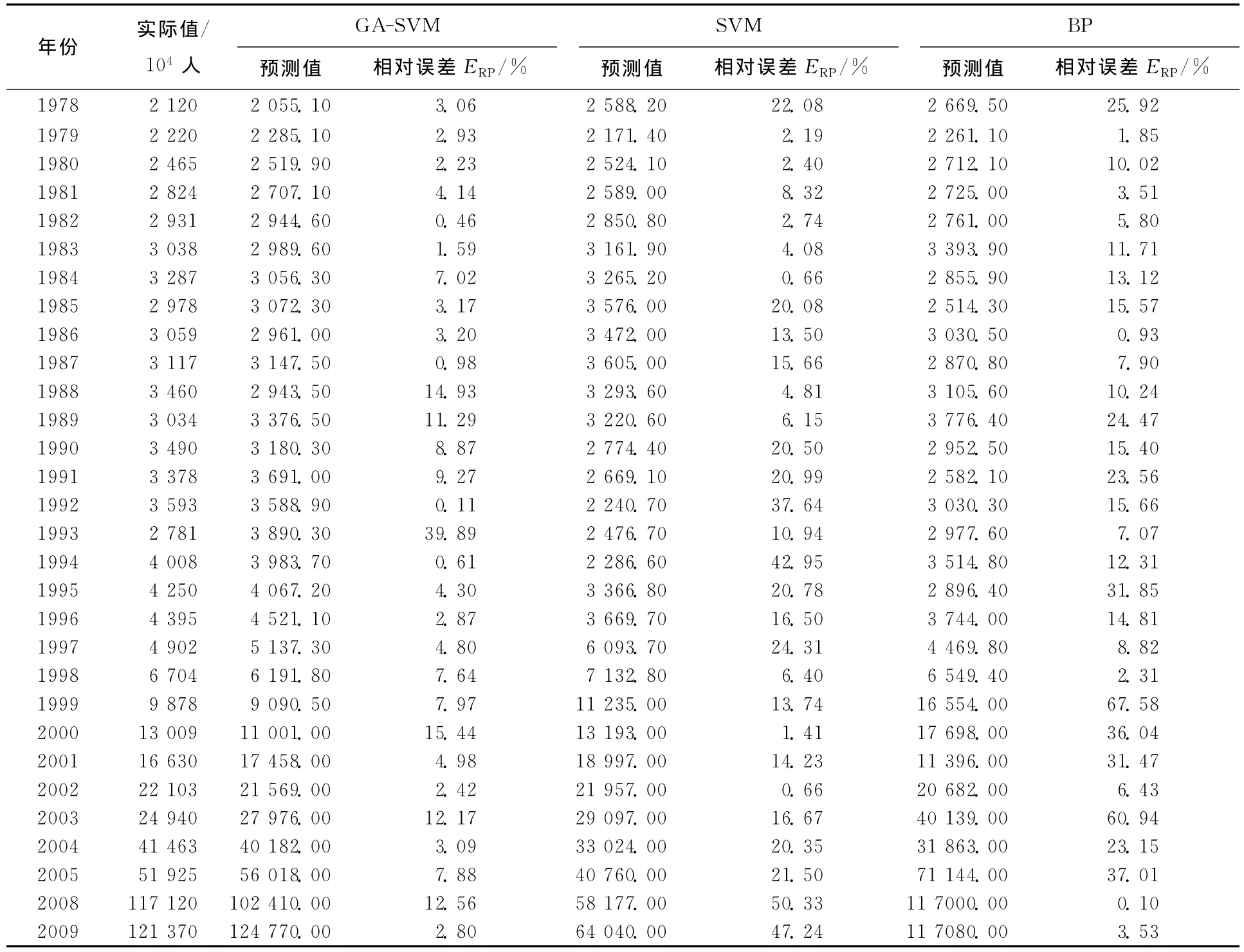
表2 GA－SVM及传统SVM、BP神经网络的预测结果比较

从表2中可以看出，基于蚁群算法的支持向量机预测模型比传统SVM和BP神经网络模型效果明显要好，而传统SVM模型效果略好于传统BP神经网络。这是因为SVM方法具有全局最优性，不会陷入局部最小点，避免了传统神经网络方法的缺陷，提高了预测精度。而基于蚁群的支持向量机方法，由于对影响支持向量机预测精度的重要参数c、ε和σ进行了基于蚁群算法的连续空间的优化搜索，避免了人工进行参数选择时需要依赖经验的缺陷，从而明显提高了预测精度。仿真结果也表明，采用蚁群算法优化参数后的支持向量机模型比传统支持向量机在预测时具有更高的精度和更强的泛化能力，即利用蚁群算法对支持向量机的参数进行优化搜索的方法是可行有效的。

4 结束语

本文提出了基于蚁群算法支持向量机的公路客运量预测方法。支持向量机以统计学为基础，在小样本、高维、非线性预测领域有着很好的应用效果，但其预测效果很大程度上取决于其参数的选取，因此考虑应用蚁群算法来优化支持向量机的训练参数，从而得到了基于蚁群算法的支持向量机的公路客运量预测模型；以北京市1978—2009年的公路客运量数据作为算例，并与BP神经网络和传统的SVM预测法相对比，验证了基于蚁群的支持向量机预测模型拟合程度更强，预测精度更高，是一种可行有效的公路客运量的预测方法。研究结果说明基于蚁群算法进行支持向量机参数优选的方法是有效的，具有一定的实际应用价值。

［1］ 刘 芹.基于最小二乘支持向量机的城市客运量预测模型［J］.交通与计算机，2007，25（5）：50－53.

［2］ 陈 荔，马荣国.基于支持向量机的都市圈客运量预测模型［J］.交通运输工程学报，2010，10（6）：75－80.

［3］ 文培娜，张志勇，罗 彬.基于BP神经网络的北京物流需求预测及分析［J］.物流技术，2009（6）：91－93.

［4］ Venkoba R B，Gopalakrishna S J.Hard grove grind ability index prediction using support vector regression［J］.International Journal of Mineral Processing，2009，91（12）：55－59.

［5］ Liu Sheng，Li Yanyan.A novel predictive control and its application on water level system of ship boiler［C］／／International Conference on Innovative Computing，Information and Control，2006：8.

［6］ 中国统计出版社.北京市2010年度统计年鉴［EB／OL］.［2011－03－20］.http：／／www.bjstats.gov.cn／nj／main／2010－tjnj／index.htm.

［7］ 耿 睿，崔德光，徐 冰.应用支持向量机的空中交通流量组合预测模型［J］.清华大学学报：自然科学版，2008，48（7）：1205－1208.

［8］ 魏 俊，周步祥，林 楠，等.基于蚁群支持向量机的短期负荷预测［J］.电力系统保护与控制，2009，37（4）：36－40.

［9］ 曹占辉，李言俊.基于支持向量机和蚁群算法的空间目标分类［J］.航空计算技术，2008，38（3）：15－18.

［10］ Dorigo M，Maniezzo V，Colorni A.Ant system：optimization by a colony of cooperating agents［J］.IEEE Transaction on Systems，Man，and Cybernetics：Part B，1996，26（1）：29－41.

［11］ 倪丽萍，倪志伟，李锋刚，等.基于蚁群算法的SVM模型选择研究［J］.计算机技术与发展，2007，17（9）：95－98.

［12］ 张志涌.精通MATLAB 6.5版教程［M］.北京：北京航空航天大学出版社，2003：250－257.