二次均匀B样条曲线的新扩展及应用

郭怀天， 黄有度

（合肥工业大学 数学学院，安徽 合肥 230009）

0 引 言

曲线曲面表示是计算机辅助几何设计中一个重要的研究课题，其中分段二次均匀B样条曲线是形式最简单的也是最常用的样条曲线之一，然而对给定控制顶点，它的位置是确定的，如果要调整曲线的形状，需要调整多边形。有理Bézier曲线和NURBS曲线通过权因子不改变控制顶点，但是它们也存在一些局限性，如计算比较复杂、求导求积不方便等。虽然二次B样条构造简单，但其是C连续的而且曲线不能调整，所以使用有一定的局限性。

文献［1］给出了带有单个参数的调配函数，也达到了G2、G3连续。但比起本文给出的2个参数来说不是那么灵活；文献［2］给出了带有2个三次B样条调配函数的基；文献［3］给出带2个参数的G1连续三次多项式曲线，也增加了曲线设计的灵活性，但是没有达到G2、G3连续，没有给出高次的形式，所以不能满足更高次的连续。本文构造了带有2个局部参数λi、μi的分段多项式样条新曲线，它是以二次均匀B样条曲线为特殊情形，可以有很多种调整方式，具有很好的局部形状可调整性。

1 二次均匀B样条曲线的新扩展

1.1 调配函数的构造与性质

定义1 对任意t∈［0，1］，λi，μi∈R，称关于t的多项式（1）式为带参数λi、μi的三次调配函数，即

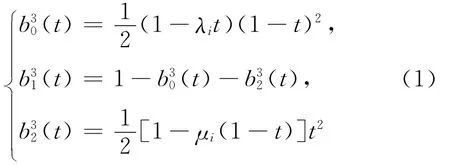
定义2 对任意t∈［0，1］，λi，μi∈R，称关于t的多项式（2）式为带参数λi、μi的四次调配函数，即

定理1 对定义1、定义2中调配函数bki（t）（i＝0，1，2；k＝3，4），有如下结论：

（2）当－2≤λi，μi≤1时，t∈［0，1］，bki（t）≥0，i＝0，1，2；k＝3，4。

证明 直接计算可得结论（1），由n次多项式在［0，1］上非负的充分条件可得结论（2），证毕。

事实上，当λi＝μi≠0时，文献［1］给出的调配函数是本文的特例，λi＝μi＝0时，三次调配函数就退化成二次均匀B样条基函数。因此，定义1所示三次调配函数是二次均匀B样条基函数的扩展，同时四次调配函数变成了λi＝μi＝1时的三次调配函数，因而它们都可以看成是二次均匀B样条基函数的扩展。

定义3 对t∈［0，1］，λi，μi∈R。称关于t的多项式（3）式为带参数λi、μi的n次调配函数，即

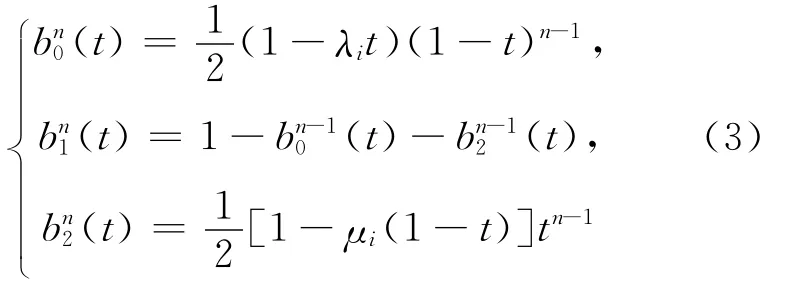
定理2 对调配函数（3）式，有如下结论：

（2）当－2≤λi，μi≤1时，t∈［0，1］，bni（t）≥0，i＝0，1，2。

证明 同定理1的证明。

1.2 曲线的构造及性质

由定义1可以定义带有局部形状控制参数λi、μi的多项式曲线。

定义4 给定控制顶点Pi∈Rd（d＝2，3；i＝0，1，…，n）和节点u0＜u1＜…＜un＋1，对u∈［ui，ui＋1］（i＝0，1，…，n－2），定义多项式曲线段：

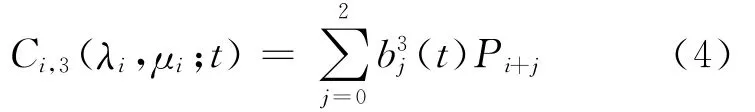
其中，t＝（u－ui）／hi；hi＝ui＋1－ui；b3j（t）为（1）式所定义的三次调配函数。定义多项式曲线：

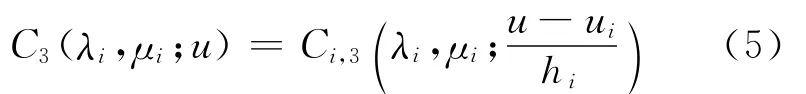
其中，u∈［ui，ui＋1］。

曲线C3（λi，μi；u）是定义在［u2，un－2］上的带局部参数λi、μi的分段三次多项式曲线，是二次均匀B样条曲线的扩展。同样利用四次调配基函数也可以定义四次多项式曲线。

定理3 当λi，μi∈［－2，1］（i＝0，1，…，n－2）时，曲线C3（λi，μi；u）是G1连续的，若曲线每相邻两段 Ci，3（λi，μi；t）、Ci＋1，3（λi＋1，μi＋1；t）的形状 参 数 满 足 μi＝λi＋1，则 C3（λi，μi；u）是 C1连续的。

证明 由（1）式、（4）式直接计算，可得：

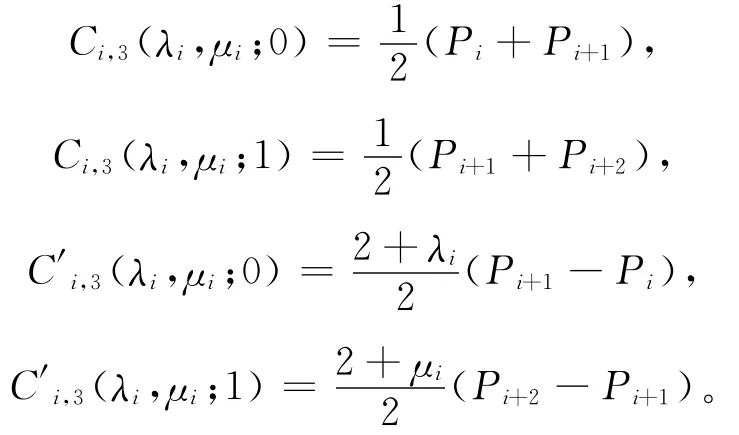
显然，当λi，μi∈［－2，1］（i＝0，1，…，n－2）时，Ci，3（λi，μi；1）＝Ci＋1，3（λi＋1，μi＋1；0），且 C′i，3（λi，μi；1）＝KiC′i＋1，3（λi＋1，μi＋1；0），其 中 Ki＝（2＋λi＋1）／（2＋μi），故其是G1连续的。若μi＝λi＋1，则 Ki＝1，从而C3（λi，μi；u）是连续的。

综上所述，可以看出曲线 Ci，n（λi，μi；t）是在曲线Ci，n－1（λi，μi；t）的基础上，对二次 B 样条曲线的进一步扩展。

定理4 当λi，μi∈［－2，1］（i＝0，1，…，n－2）时，曲线C4（λi，μi；u）是G2连续的。

证明 由（2）式、（4）式直接计算，可得：

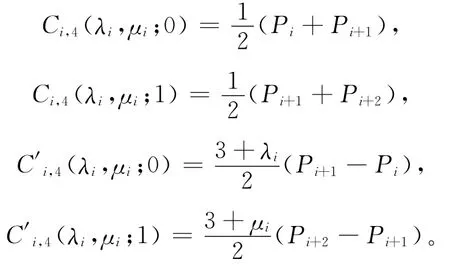
显然，当λi，μi∈［－2，1］（i＝0，1，…，n－2）时，Ci，4（λi，μi；1）＝Ci＋1，4（λi，μi；0），且 C′i＋1，4（λi＋1，μi＋1；0）＝K1C′i，4（λi，μi；1），其中，进一步计算，得

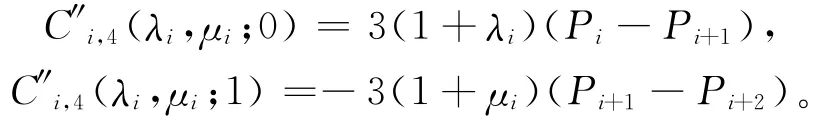
由定理3、定理4可以看出，当λi＋1、μi满足一定关系时，C3（λi，μi；u）、C4（λi，μi；u）可以分别达到G2、G3连续，而且，它们也与分段二次B样条曲线的结构相同。通过定理可知，四次曲线将三次曲线的连续性提高了一阶［4－8］。

2 参数的几何意义

当固定λi，参数μi逐渐增大（或者减小）时，曲线逐渐靠近（或者远离）控制多边形的边，如图1所示，其中曲线从上到上依次μi＝－1.5，0.1。

同样当固定μi，参数λi逐渐增大（或者减小）时，曲线逐渐靠近（或者远离）控制多边形的边。

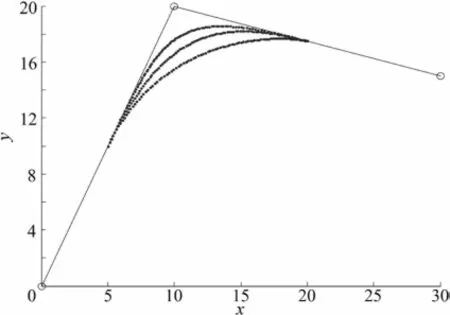
图1 固定λi＝0.5，μi变化时的曲线

此外，2个参数同时改变可以实现更加灵活的逼近方式，如一个增大一个减小，同时增大或者减小。根据λi、μi的几何意义，可以根据需要方便地进行曲线设计。而且利用所给调配函数运用张量积的方法可以推广到曲面，本文不再讨论。

3 扩展曲线的应用

利用定义1所给的三次调配基函数给出实例图形，如图2所示，所得的分段曲线可以通过参数λi、μi进行调整，当λi＝μi＝0时，即为二次均匀B样条，四次和更高次的调配可以满足更好的连续性。图2中利用了文献［1］给的控制顶点，即V0＝（0，0），V1＝ （10，20），V2＝ （30，15），V3＝（20，5），V4＝（60，0）。

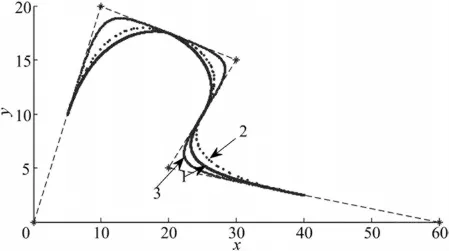
图2 参数取不同值的曲线

图2中，曲线1的λi＝（0.5，－1.5，0.5），μi＝（－1.5，0.5，0.5），i＝0，1，2；曲 线 2 的λi＝μi＝0，i＝0，1，2；曲线3的λi＝μi＝1，i＝0，1，2。

［1］ 刘长明，檀结庆.二次均匀B样条曲线的扩展［J］.合肥工业大学学报：自然科学版，2004，27（5）：459－462.

［2］ 胡 钢，刘 哲.三次均匀B样条曲线的新扩展及应用［J］.计算机工程与应用，2008，44（32）：161－164.

［3］ 殷 明，刘 丽，陈国琪.一类可调控的G1连续分段三次多项式曲线［J］.安徽农业大学学报，2005，32（2）：258－262.

［4］ 施法中.计算机辅助几何设计与非均匀B样条［M］.北京：高等教育出版社，2001：166－302.

［5］ 王国瑾，汪国昭，郑建明.计算机辅助几何设计［M］.北京：高等教育出版社，2001：18－56.

［6］ 韩旭里，刘圣军.三次均匀B样条曲线的扩展［J］.计算机辅助设计与图形学报，2003，15（5）：567－578.

［7］ 严兰兰，黄 涛，梁炯丰.3种带形状参数的二次三角样条曲线［J］.合肥工业大学学报：自然科学版，2010，33（4）：632－636.

［8］ 张三元.一种G2连续的二次曲线样条插值方法［J］.计算机辅助设计与图形学报，2000，12（6）：419－422.