地面平面场RCS测量异地定标误差分析

吴鹏飞 许小剑

(北京航空航天大学电子信息工程学院 北京 100191)

1 引言

全尺寸目标静态测量是测量目标雷达散射截面(Radar Cross Section,RCS)的方法之一，对目标散射特性的研究有十分重要的意义[1]。全尺寸目标通常为大型目标，为满足远场条件，场地的纵向测量距离很大。但是目标的架设高度有限，所以目标容易受到地面反射波的影响[2]。在对目标、雷达和地面特性进行合理的设计后，可以利用地面反射使目标上集中更多的能量。这种通过地面反射波来增加雷达系统增益的场地被称为地面平面场[3]。由于测量目标是大型目标，为了减少定标过程中定标体和目标交替安装的次数，地面平面场中通常用相对定标法进行定标，而且采用将定标体安放在独立支架上的异地定标技术，以降低定标过程的时间成本和操作复杂度[4]。

在IEEE标准1502-2007[5]中，将影响RCS测量不确定度的因素分解为平均辐照度、系统漂移等13项误差，其中定标体的RCS不确定度是重要的因素之一。在考虑距离对于相对定标不确定度的影响时，也仅考虑了自由空间的情况。据作者所知，国内外文献中未见研究地面平面场条件下异地定标的误差问题。

本文主要研究在地面平面场中测量目标 RCS时，由于异地定标产生的误差。首先分析了地面平面场的基本原理，得到其基本特性，然后推导出地面平面场异地定标的误差公式。最后进行计算机仿真，研究异地定标误差受定标体测量距离、测量频率以及天线波束宽度等参数变化的影响，并给出了分析结论。

2 地面平面场的基本原理

地面平面场的几何关系示意图如图1所示。

图1 地面平面场几何关系示意图

A为雷达天线所在的位置，T为待测目标所在位置，P为反射波在地面上的反射点。地面平面场中，电磁波可以沿4条不同的路径传播，分别为直接路径ATA，间接路径APTPA，双向路径APTA和ATPA[6]。根据几何关系，路径AT的长度D为

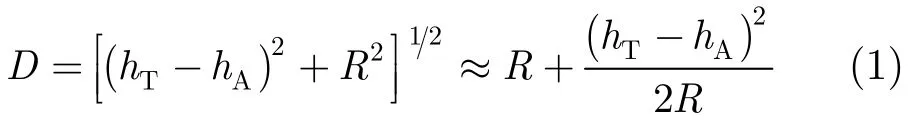
反射波路径APT的长度I为

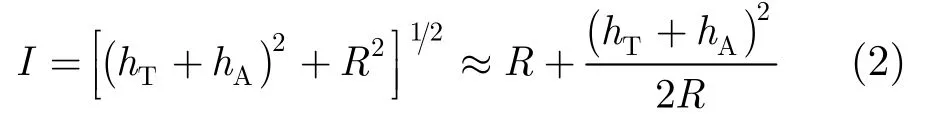
D和I两者的路程差δ为

地面平面场中，天线高度hA和目标高度hT均远小于测量距离R。所以在分析时采取以下3个原则：

(1)忽略由于路程差导致不同路径电磁波在幅度上的衰减，主要考虑路程差对相位造成的影响[7]。

(2)双站角γ很小，在选用金属球作为定标体时，忽略目标上直射波和反射波到达角的差异。

(3)入射擦地角φ很小，且通常P点附近的地面都经过人工处理，所以假设地面的反射系数ρ=− 1[8]。

为了简化对本问题的讨论，先仅考虑幅度定标的情况。若E0为自由空间中天线接收到距离R处的目标散射场场强，E为地面平面场中的场强，则[9]

式中e−j2kD项是直接路径的回波；2ρe−jk(D+I)项是双向路径的回波，由于两条双向路径刚好相反，所以乘以因子 2;ρ2e−j2kI项是间接路径的回波，由于这条路径两次照射到地面并反射，所以乘以地面反射系数的平方。k=2π λ为波数，λ为雷达波长。

为了使地面反射波达到增强照射增益的效果，各路径的相位保持一致，需要满足

式中m为奇数，即m=1,3,5⋅⋅⋅。在地面平面场中，通常取m=1。

在实际测量中，由于所使用的天线具有很强的方向性，这给地面不同距离处的场强分布带来了不可忽视的影响。假设天线的方向图是天线视线的一个旋转体图形。天线的方向性函数表示为f(θ),θ是偏离视线的角度。在式(4)中引入天线方向图的影响，有

式中，θD和θI分别表示直射路径和反射路径相对于天线视线的夹角。

本文中令目标在地面平面场中的回波功率P与自由空间的功率P0比值为K，并称之为增益因子。其表示的是由地面平面场几何关系和天线方向性综合产生的回波功率的增益。根据式(3)、式(5)、式(6)，K为

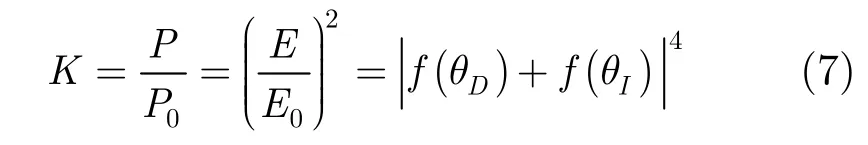
3 地面平面场异地定标误差分析

3.1 异地定标原理

首先在不考虑地面反射的情况下，对自由空间中异地定标的基本原理进行分析。异地定标几何关系示意图如图2所示。

图2 异地定标示意图

此时，定标体和待测目标均满足雷达方程

若目标RCS为σT，定标体RCS为σC，则两者之间的关系为

式中RC和RT分别为定标体和待测目标的测量距离，PrC和PrT分别为定标体和目标的接收功率，LTLC为系统传输损耗项。等号右侧的各个参数均可以通过计算或测量得到，所以可以计算出目标的RCS，完成定标过程。

3.2 地面平面场中的异地定标

在地面平面场中，因为存在地面反射路径，所以目标实际测量的接收功率PmT和自由空间内的接收功率PrT满足

式中KT为目标处由地面平面场几何关系和天线方向性综合产生的增益因子。

同理，定标体实际测量的接收功率PmC和自由空间内的接收功率PrC满足

式中KC为定标体处的增益因子。由于定标体和目标的放置位置不同，所以通常定标体的增益因子KC与目标的增益因子KT不同。

根据式(9)、式(10)、式(11)，地面平面场中目标RCS与定标体RCS之间的关系为

需要注意的是，无论是待测目标还是定标体，在安放时与天线的关系均要满足式(5)，以获得最好的测量效果。待测目标的测量距离RT和高度hT通常根据地面平面场的客观条件确定，然后按照实际的测量频率(波长)确定天线高度。固定天线高度和测量频率后，定标体的测量距离RC和高度hC的关系为

对于不同的定标体测量距离RC(高度hC)，定标体的增益因子会有所变化。异地定标产生的增益因子误差也会随着定标体的测量距离变化。

3.3 宽带测量的定标误差

点频测量时，一般把天线高度和目标高度调整在该频点上，满足式(5)的地面平面场条件。宽带测量时，一般把天线高度和目标高度调整在中心频率处。下面分析宽带测量时的定标误差问题，点频测量的相位定标误差与宽带中心频率处的相位定标误差基本相同。

对于中心频率f0，带宽为B的宽带测量，根据式(6)，回波信号可表示为

根据式(14)，待测目标在测量频率为f时，有

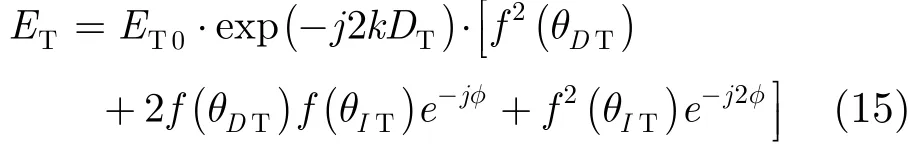
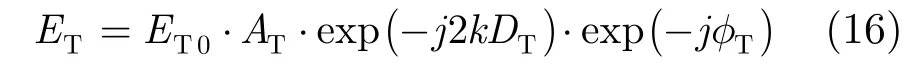
相似地，对于定标体，有

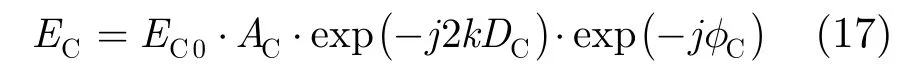
当测量频率等于中心频率时，φ,φT,φC恰好均为 0。此时相位定标误差与自由空间中的相位定标误差一致，为

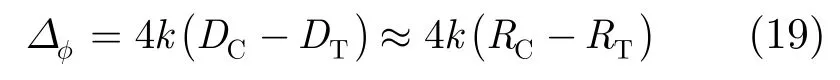
当测量频率在带宽内变化时，AT,AC,φT,φC均随频率改变，此时情况比较复杂，限于篇幅不进行详细讨论。

4 计算机仿真分析

为了研究定标体增益因子KC和误差KCKT随测量距离等参数的变化，进行计算机仿真。仿真条件如下：目标的测量距离RT=2000 m，目标高度hT=10 m。天线的半功率点波束宽度θ3dB=1°，天线方向性函数为，其中,d是天线直径。

在此条件下，首先对不同频率下不同定标体测量距离的增益因子和误差进行计算。图3所示为S波段(雷达频率3 GHz)、C波段(6 GHz)、X波段(10 GHz)在距离RC的范围从500 m至2000 m之间的KC和KCKT。其中 2000 m处的定标体增益因子KC就是待测目标的增益因子KT。

通过图3可以看出，随着定标体距离的增大，增益因子逐渐增大，误差逐渐趋向于 0。当测量频率较高时，增益因子和误差随距离的变化不明显。例如，在X波段，对于500 m至2000 m的定标体距离范围内，误差均不超过0.4 dB，超过600 m时，误差小于0.2 dB；而在S波段，定标体距离为500 m时，误差可达3.6 dB，在超过1200 m时才可满足0.2 dB误差要求。但是在实际选取定标体放置位置时，也不宜过分靠近目标，以防止定标体对目标的遮挡等干扰效果增强，影响测量精度。关于定标体对目标遮挡的影响，在文献[4]中已有类似的研究，此处不赘述。

图4所示为距离CR为700 m,1000 m和1500 m时的3个不同距离点，频率在3 GHz至15 GHz之间增益因子和误差的变化。可以看出，在同一测量距离下，KC随测量频率增大而增大。当定标体放置位置靠近目标放置位置时，即定标体距离与目标距离差距不大时，误差随频率的变化不明显。当定标体距离为1500 m时，对于3 GHz至15 GHz的频率段，误差在0.05 dB以内。

将测量频率固定为3 GHz，研究增益因子和误差随天线波束宽度的变化。图 5所示为距离CR为700 m,1000 m和1500 m时的3个不同距离点，天线的波束宽度3dBθ在0.8°至2°之间增益因子和误差的变化。

图3 不同频率下定标参数随距离的变化

图4 不同测量距离下定标参数随频率的变化

图5 不同测量距离下定标参数随天线波束宽度的变化

通过图5可以看出，随着天线波束宽度变宽，增益因子逐渐增大。当定标体放置位置靠近目标放置位置时，误差随波束宽度的变化不明显。但是改变天线波束宽度会影响到天线的固有增益，即式(8)雷达方程中的G，从而影响到整体的定标增益，所以在实际测量中要综合考虑各个方面的因素，选取合适的天线波束宽度。

5 总结

本文主要研究地面平面场 RCS测量过程中异地定标产生的误差。从地面反射和天线的方向性这两个地面平面场的主要特性入手，研究了不同测量位置的增益因子的变化，以此修正定标体RCS和目标RCS之间的换算关系，并计算出放置在不同位置定标体与目标增益因子之间的差异所造成的定标误差。其结果可作为地面平面场的设计、建造和实际使用过程中定标距离等参数选择的基本依据。在宽带测量时，定标误差随带宽内频率的变化仍需要进行更为详细的研究。