基于投影矩阵法的阵列天线波束形成方法
刘肖萌 高文军 邓云凯 王 乐② 焦军军
①(中国科学院电子学研究所航天微波遥感系统部 北京 100190)
②(中国科学院研究生院 北京 100049)
1 引言
现代通信、广播和雷达系统要求天线具有波束扫描或波束重构能力,实时实现方向图赋形的要求,满足通信分集、优化信息交换和扩展雷达系统功能的需求。通过调整阵列天线单元的激励系数来实现天线的特定辐射方向图。目前常用方法有泰勒综合法等[1],共轭匹配法[2],最小二乘法,投影矩阵法[3],遗传算法[4],粒子群算法[5]等。其中泰勒综合法只能优化幅度激励系数。共轭匹配法和最小二乘法只能优化复数激励系数,不能添加仅相位或仅幅度控制约束。遗传算法是一种进化算法,粒子群算法与其类似,都需要建立种群,根据一定的策略迭代寻优,但是由于种群的规模与自变量个数近似成正比,所以自变量个数不能过大。对于阵列天线的激励系数优化问题,自变量个数的限制约束了阵列中单元的个数,若阵列规模较大(由成百上千个单元组成),则使用遗传算法或粒子群算法优化激励系数的计算时间代价较大。而投影矩阵法具有快速、高效的特点,对阵列规模并没有限制,可以方便地实现多约束条件,不要求各单元具有相同辐射方向图,适用于一般性阵列天线的波束综合。
投影矩阵法是一种线性代数方法,对于由线性方程表示的系统,可以得到最优解。这种方法已经被应用于信号处理领域和其它的工程领域[6]。然而不加修改的将投影矩阵法应用于阵列的综合问题上,会存在稳定性和收敛性问题。Bhattacharyya A K研究了这些问题,并且给出必要的修正,成功地应用到波束综合问题上[3]。考虑一般性阵列,即各单元具有不同的辐射方向图。运用正交矢量空间的概念,定义与阵列综合相关的投影矩阵。通过合理地定义远场抽样空间,保证矩阵具有较好的条件数,可得到一致收敛的解。
本文首先介绍复系数投影矩阵法和仅相位投影矩阵法,并对其目标函数进行改进,强调了目标波束的形状、副瓣电平分布等细节。传统的投影矩阵法在更新误差方向图,使用的是增益方向图,需要根据经验,较准确地估计期望方向图的增益值,若估计值不准确,则对方向图形状的约束效果会变差。因此,本文采用归一化的期望方向图,强调了方向图形状的一致性,加强了对波束形状的约束。另外,由于一般仅对副瓣电平的峰值要求限制,而不关心副瓣区域的方向图形状细节。因此,采用上、下界掩模表示方向图的期望取值区域,而不是使用一个取值固定的期望方向图曲线,在一定程度上加快了算法迭代收敛速度。本文将投影矩阵法推广应用,形成仅幅度控制技术,并进一步对多目标波束同时综合优化,包括仅相位控制下,阵列天线的多波束同时综合;以及阵列天线多个子孔径波束与全孔径波束同时综合。算例表明,该类方法均可快速得到收敛解。
本文的第2节介绍投影矩阵法的理论和收敛条件,第3节阐述了在仅相位控制约束或仅幅度控制约束下,应用于阵列天线单波束综合的改进投影矩阵法,第4节介绍了应用于阵列天线多波束同时综合的改进投影矩阵法,第5节给出了仿真算例,第6节为结论。
2 投影矩阵法
2.1 投影矩阵法的理论基础
在已知阵列天线的几何结构及目标方向图指标参数的情况下,投影矩阵法可用于优化阵列天线的单元激励系数,实现指定的波束。假定阵列天线的单元个数为N,Fd(u,v)是期望得到的远场增益方向图。目的是找到一个激励集合An(n=1,2,…,N),满足如下方程式:

其中u=sinθcosφ,v=sinθs inφ,k是自由空间的波数,(θ,φ)是远场观察点的球坐标分量。An,(xn,yn),En(u,v)分别是第n个单元的复数激励系数、位置坐标和辐射方向图。在式(1)中忽略了随距离变化的项exp(−jkr)/r和时间变化因子exp(jω t),r为观察点与阵列天线相位中心之间的距离。
第n个单元的辐射方向图可以近似为是单元口径场分布的傅里叶变换。
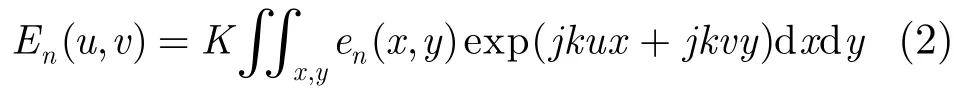
其中en(x,y)是在局部坐标系下的第n个单元的激励分布。常数K可以根据近似增益值表示为

其中λ是波长。
为了求解出An,选取M个远场点,得到M个约束方程,其矩阵形式如下:

其中Fdm是的缩写,的是第m个观察点的直角坐标分量。Fd,T,A分别是期望方向图、阵中各单元方向图、激励系数的矩阵形式。
在最小二乘的意义下,当误差矢量与T矩阵的列向量空间正交时,可以得到最优解,如图1所示(图中假设阵列由两个单元组成,N=2,M=3,T1和T2是T矩阵的第1列和第2列)。即激励矢量满足如下法方程:
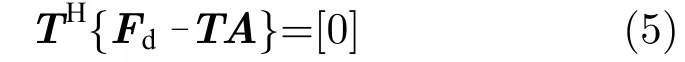
其中大括号内部的矢量是误差矢量。式(5)可用于求解激励矢量A


图1 阵列综合问题的矢量空间图
定义矩阵P为P=T(THT)-1TH,即为投影矩阵,当它作用于一个矢量时,得到该矢量在T列向量空间的投影矢量[6]。且原方程的最优解是矩阵方程PFd=TA的准确解。
2.2 投影矩阵法的流程
由于一般只给定期望方向图的幅度分布,为了得到远场的相位分布,采用一种迭代方法。首先假定一个归一化于输入功率的试探激励矢量A(1)。用A(1)代替式(4)右边的A,得到相应的远场矢量F(1)。很明显,在大多数远场点上,F(1)的单元不同于Fd。计算误差方向图

其中Fm(1)是F(1)的第m个分量,ΔFm是ΔF的第m个分量,Fdm是Fd的第m个分量。
但使用式(7)来更新误差方向图,需要较准确的估计期望方向图的增益值,若估计不准确,则对方向图形状的约束效果会变差。因此,本文采用归一化的期望方向图,强调了方向图形状的一致性,加强了对波束形状的约束。另外,一般仅对副瓣电平的峰值要求限制,而不关心副瓣区域的方向图形状细节,因此,采用上、下界掩模表示方向图的期望取值区域,促进算法迭代收敛速度。计算误差方向图为
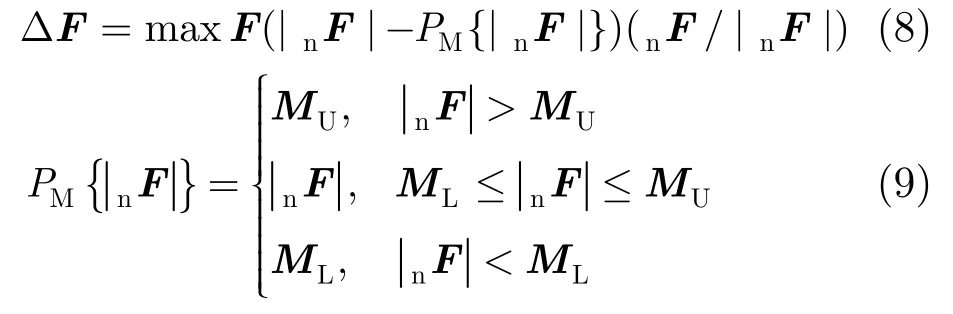
其中Fmax是方向图中最大值,Fn是归一化方向图,PM{|nF|}是由掩模定义的投影算子,PM算子将归一化方向图投影到由掩模定义的区域内。MU是期望方向图的上界掩模,ML是期望方向图的下界掩模。
根据投影矩阵法,可求解出增量激励系数,即
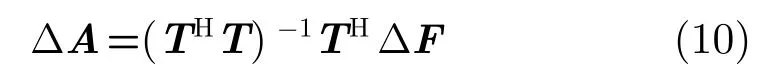
得到增量激励系数矢量后,可更新复数激励矢量为
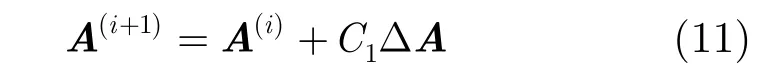
其中A(i)和A(i+1)分别为迭代第i步、第(i+1)步的激励系数,C1是步长。归一化新的激励矢量后,重复整个过程,直至得到令人满意的远场方向图或达到最大迭代次数。
2.3 收敛条件
上文描述的算法涉及到矩阵τ=THT逆矩阵的求解。若此矩阵具有较大的条件数,用数值方法求解该矩阵的逆就会存在不稳定的问题。
T矩阵的元素主要由阵列单元的位置和远场观察点决定。通过合理选择观察点角度取值范围和角度间隔能够保证算法的收敛性。根据单元大小和阵列长度来决定取样范围和取样间隔。观察角度范围必须大于各单元的波束宽度,u(v)空间抽样区域的范围应大于2/dπ,其中d为单元间距。角度间隔必须小于相控阵全口径均匀分布的波束宽度,即u(v)空间的抽样间隔应小于2/()Ndπ,Nd可由阵列长度代替。从而保证τ具有较小的条件数,从而使得求解过程具有收敛性。
3 应用于阵列天线单波束形成的投影矩阵法
采用基本的投影矩阵法,可实现阵列天线单波束综合,但优化的激励系数为复数形式,并不能单独优化相位激励系数(保持幅度激励系数不变),或单独优化幅度激励系数(保持相位激励系数不变)。为了在仅相位控制或仅幅度控制下,完成阵列天线方向图的综合,在投影矩阵法的迭代过程中,需改变激励系数矢量的更新方式。
3.1 仅相位投影矩阵法
采用只改变馈电相位分布的仅相位加权方法可使其不改变原有功率分配馈电网络和不增加新设备的情况下,利用计算机控制移相器值的改变实现波束赋形,是非常经济而且可行的方法。Bhattacharyya A K在文献[3]中使用仅相位控制方法,实现了反射面天线的面赋形。使用类似的激励系数更新方式,实现仅相位控制下的单波束综合。
在仅相位控制的约束下,在投影矩阵法的迭代中,只更新激励系数的相位分布[3,7,8],即
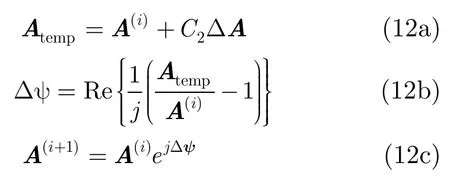
其中C2为步长,A(i)和A(i+1)分别为迭代第i步、第(i+1)步的激励系数,Atemp为临时变量。
3.2 仅幅度投影矩阵法
使用阵列天线产生极低副瓣的方向图或产生非常接近于选定形状的方向图,也可以通过只调整阵列幅度激励系数的方式。目前有很多经典地求解阵列幅度激励系数的方法,包括傅里叶变化法、Woodward综合技术、切比雪夫综合法、泰勒综合法等[1]。
采用投影矩阵法来实现仅幅度控制下的波束综合,也可有效地降低副瓣电平。在迭代中,只更新激励系数的幅度分布,保持相位激励系数不变[9],即

其中C3为步长,A(i)和A(i+1)分别为迭代第i步、第(i+1)步的激励系数。
4 应用于阵列天线多目标波束同时综合的投影矩阵法
对于阵列天线的多目标波束综合问题,需改变阵列激励系数满足的约束方程形式,用以满足多波束同时优化的要求。
4.1 仅相位控制下,阵列天线多波束综合
对于阵列天线的多波束(假设波束个数Q)综合问题,采用共用幅度分布和单独相位分布同时优化来实现波束综合,既能够保证仅相位控制,又能够提高多波束的性能。
基于投影矩阵法,构造多波束优化算法[10],在每一步迭代中包含两个子步骤,分别实现共用幅度激励系数的迭代更新和多组相位激励系数的迭代更新。根据优化结果进行阵列幅度分布加权,然后通过改变激励系数相位分布来实现多波束切换。
在共用幅度激励系数的更新子步骤中,激励系数应满足的约束方程为


在相位激励系数的更新子步骤中,激励系数应满足的约束方程为

其中Tangle为包含幅度激励信息的T矩阵。A1,A2,…,AQ是相位激励系数,可以拆分成Q个约束方程组,即
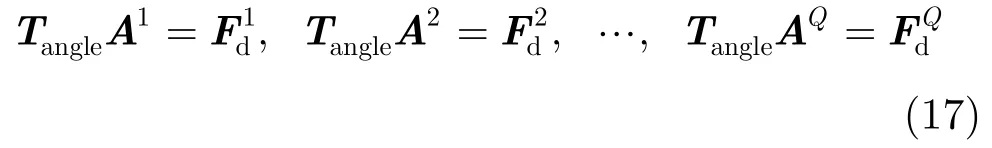
在相位激励系数更新子步骤中,相位激励系数的更新方式与式(12)相同。
4.2 仅幅度控制下,多子孔径及全孔径阵列天线多波束形成
在SAR系统中,采用方位向多相位中心多波束技术,改善方位向分辨率和测绘带宽之间的矛盾。这种SAR天线在方位向采用多子孔径技术,每一个子孔径都单独地接收回波。为了降低天线全孔径方向图和各子孔方向图的副瓣电平,要求采用仅幅度控制技术,实现这种带有子孔径结构的阵列天线的多波束综合[9]。采用仅幅度投影矩阵法,并构造多目标优化矩阵,能够有效的实现该种天线的多波束综合。
假定阵列天线单元个数为N,每个子孔径中的单元个数为N1,子孔径个数为N2,待综合的多波束个数为Q1(Q1=N2+1)。激励系数应满足的约束方程为

其中Twhole为全孔径工作时包含相位激励信息的各阵列单元的方向图,Tsub1,Tsub2,…,TsubN2元的为包含相位激励信息的子孔径中各阵列单元的方向图,Aamp为幅度激励系数,Fdwhole为全孔径工作时的期望方向图,为各子孔径单独工作时的期望方向图。在这一问题中,幅度激励系数的更新方式与式(13)相同。
5 仿真实例
5.1 仅相位投影矩阵法应用于单波束综合
线阵天线由64个单元组成,单元间距0.66λ,线阵在x轴上对称放置,在仅相位控制下,幅度激励保持均匀分布,综合出一个相对于法向扫描-3°的波束,波束宽度为 1.2°,且要求在角度范围[-10°,-7°]内副瓣电平低于-35 dB,在角度范围[-41°,-35.8°]内副瓣电平低于-50 dB。使用 6位数字移相器控制各单元的相位。
通过本文的论述,对不同氧化程度氧化石墨烯制备及湿敏性能通过实验的手段进行了相关研究,文中对样品的制备手段有详细的描述,同时通过图表的形式对样品测试结果进行展示,通过这样的方式得出实验结果,希望能为未来氧化石墨烯作为湿敏元件的发展做出一定贡献。
在2000步迭代过程中,增量激励系数的最大值收敛曲线如图2所示。从图中可以看出,随着迭代的继续,增量激励系数的最大值越来越小,并趋于一个极小的值,表明算法逐渐收敛。
在 2.3节中,讨论了投影矩阵法的收敛条件,其中观察角度范围必须大于各单元的波束宽度,即49.2509°,角度间隔必须小于相控阵全口径均匀分布的波束宽度,即1.3566°。当矩阵τ的条件数较小时,算法收敛。分别研究了观察角度范围和角度间隔对矩阵τ=THT条件数的影响,如表1所示。表1中u空间抽样区域的范围是[-umax,umax],u空间的抽样间隔为Δu。
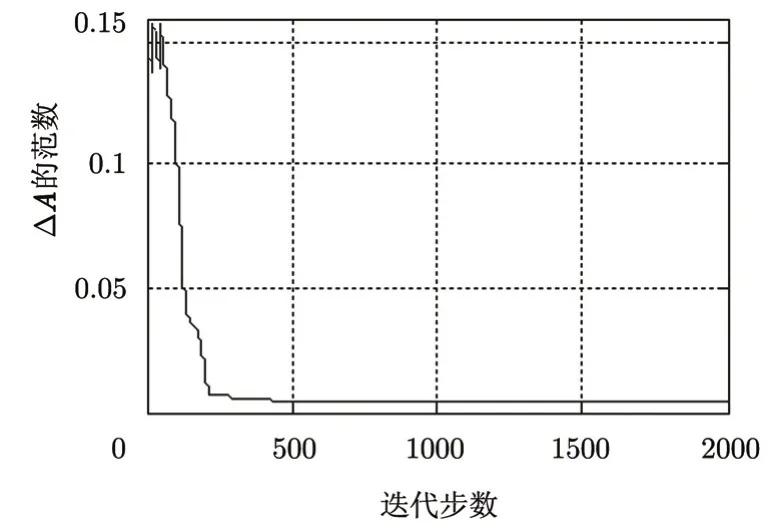
图2 增量激励系数的最大值变化曲线
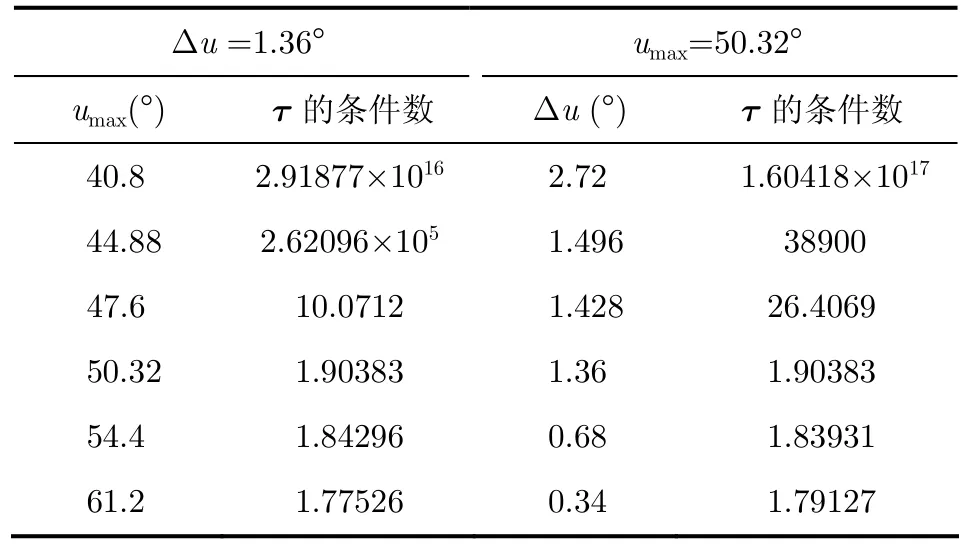
表1 矩阵τ条件数随着角度范围和角度间隔的变化情况
采用仅相位投影矩阵法得到的相位激励分布和方向图如图3所示。图3(b)和图3(c)中包括综合出的归一化方向图,上界掩模和下界掩模。线阵的增益为24.93dB,中心指向-3°。
5.2 仅幅度投影矩阵法应用于单波束综合
放置在xoy坐标面内的面阵天线,单元排列在矩形栅格上,x向由32个单元组成,单元间距0.9λ;y向由24单元组成,单元间距0.9λ。单元方向图采用其口径分布的傅里叶变换来近似。在仅幅度控制下,相位激励均为0°,期望综合出椭圆形波束,xoz面内的波束宽度为2.19°,副瓣电平低于-25 dB;yoz面内的波束宽度为2.9°,副瓣电平低于-25 dB。采用仅幅度投影矩阵法得到的幅度激励分布和归一化方向图如图4所示,增益为37.83 dB。图4(a)为面阵的幅度激励分布;图4(b)为综合出的3维等高线方向图,其中u=sinθc o sϕ,v=sinθs inϕ,单位为度;图4(c)和图4(d)显示了xoz面和yoz面内的方向图,可见副瓣电平和波束宽度均满足了设计要求。
5.3 仅相位控制下,阵列天线的多波束综合
给出一个机载SAR阵列天线的例子,天线的法向视角为65°,波束1,波束2,波束3分别照射视角范围是[76.29°,80.38°],[66.5°,72.65°],[34.99°,52.43°]的3个测绘带。为了得到最高的信噪比,同时综合3个余割平方形状的波束,得到共同的幅度激励系数和3组不同的相位激励系数,如图5所示。对应的3组方向图如图6所示。图6中,曲线s1 对应激励幅度分布为固定的泰勒加权(-30 dB副瓣电平),在仅相位控制下,分别综合3个单波束的情况;曲线s2为多波束同时综合的结果,可以看出,后者性能较佳。
5.4 仅幅度控制下,多子孔径及全孔径的阵列天线多波束形成
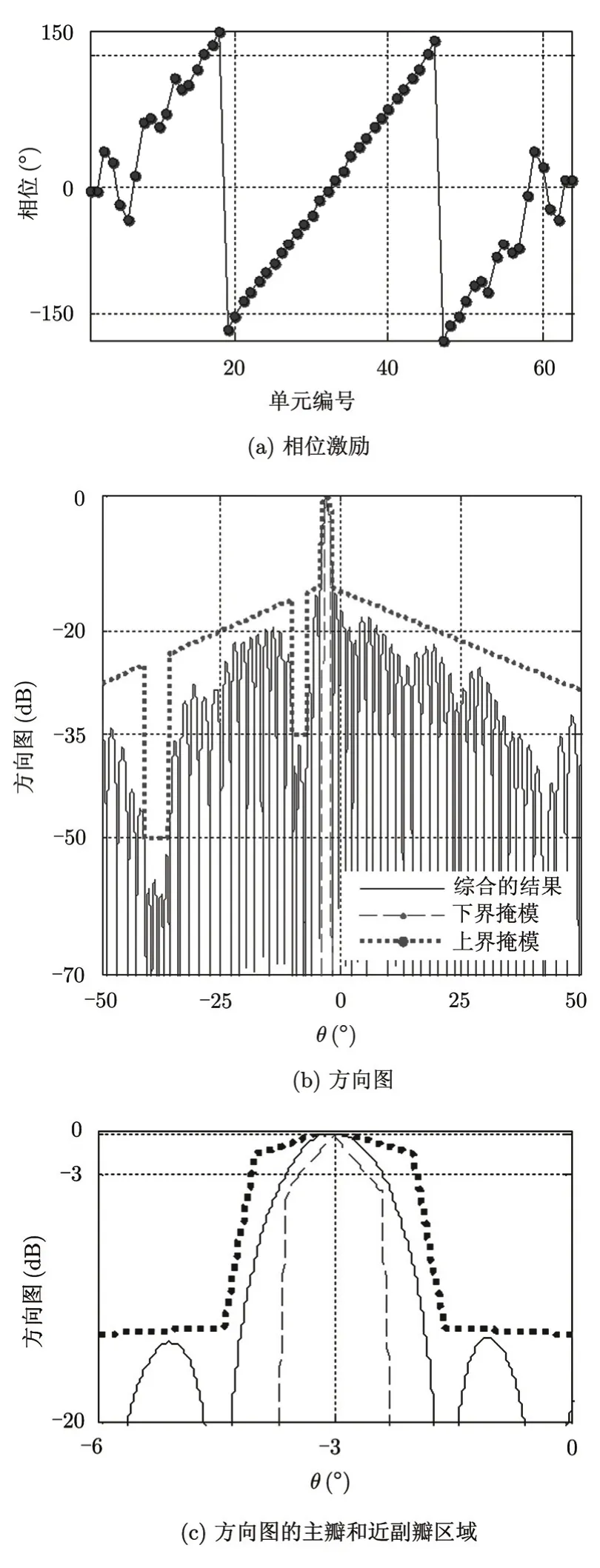
图3 展宽波束的相位激励分布和方向图
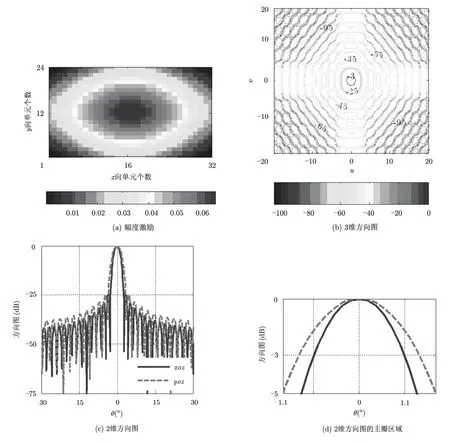
图4 波束的幅度激励分布和方向图
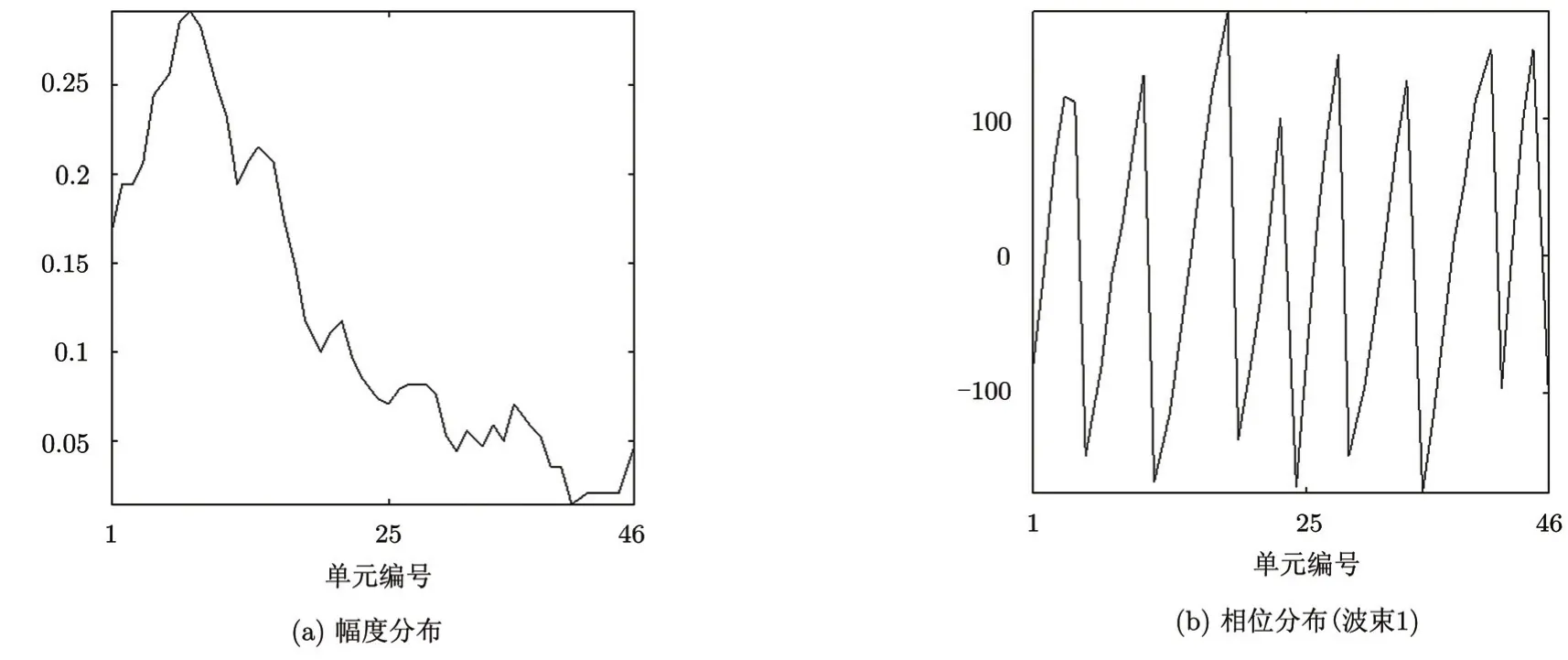

图5 三波束的幅度激励分布和相位激励分布

图6 三波束的方向图
阵列天线的单元个数是40,单元间距为0.8λ,由5个子孔径组成,每个子孔径包含8个相邻单元。全孔径工作时产生的窄波束和5个子孔径分别产生的宽波束被同时综合,得到的幅度激励分布和方向图如图7所示。其中“whole”表明是全孔径工作时得到的方向图,“B-SA1”,“B-SA2”,“B-SA3”,“B-SA4”,“B-SA5”分别表示5个子孔径分别工作时得到的方向图。全孔径的增益为24.54 dB, 各子孔径的增益约为17.85 dB。综合出的方向图副瓣电平均低于-17 dB,在仅幅度控制下,可有效地降低多波束的副瓣电平。
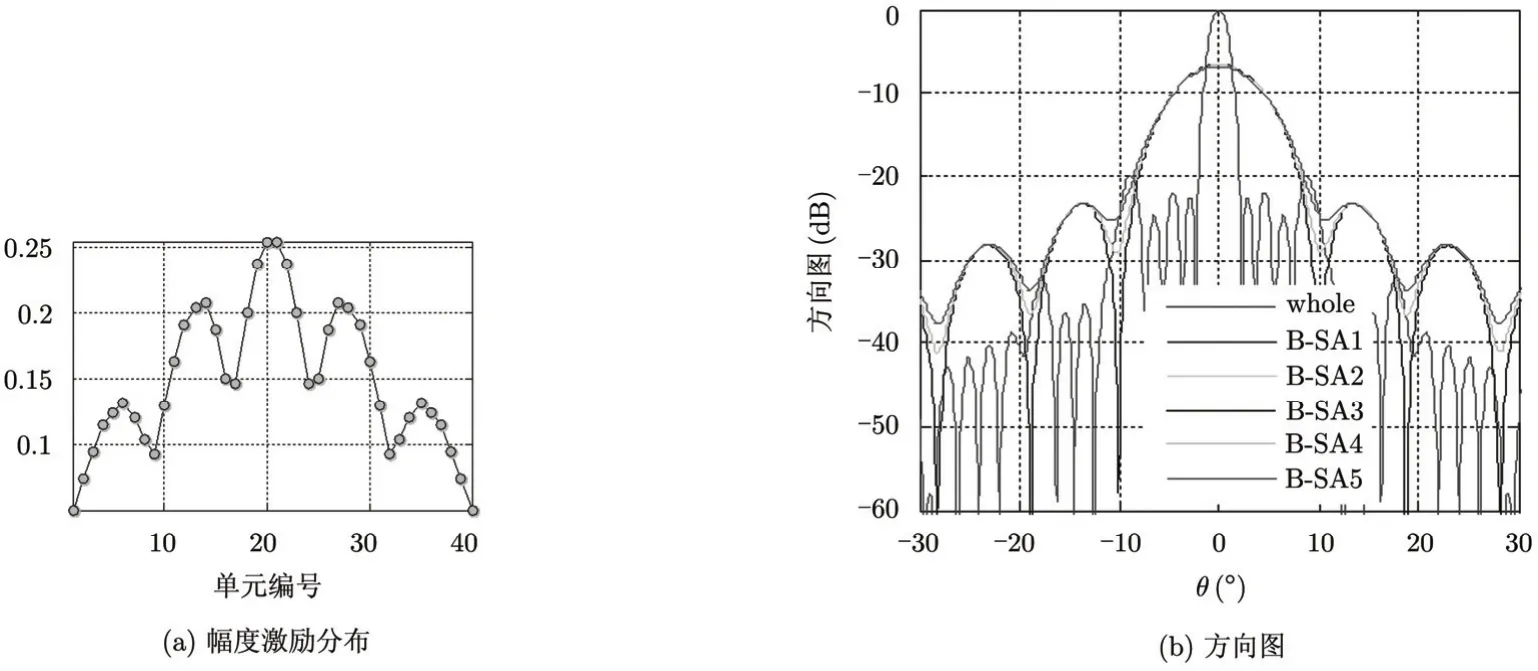
图7 多波束的幅度激励分布和方向图
6 结论
本文介绍了投影矩阵法的基本方法及其改进,可以满足仅相位控制或仅幅度控制约束,采用改进的投影矩阵法完成了阵列天线的波束综合,可根据多种不同的应用需求,采用不同的改进策略,实现阵列天线的单波束综合和多波束综合。算例仿真结果表明改进的投影矩阵法可灵活高效地实现阵列天线的波束综合。改进的投影矩阵法也可用于阵列馈电反射面天线的波束形成。

