伶仃洋河口水域纳潮特性分析
方神光, 陈文龙, 崔丽琴
(珠江水利委员会 珠江水利科学研究院, 广东 广州 510611)
伶仃洋河口水域纳潮特性分析
方神光, 陈文龙, 崔丽琴
(珠江水利委员会 珠江水利科学研究院, 广东 广州 510611)
为阐明伶仃洋河口水域纳潮现状和特性, 分别采用经验公式和建立贴体曲线坐标系下的珠江河口二维数学模型的方法, 对河口伶仃洋水域的纳潮特性进行了分析和探讨。数学模型的离散和求解采用纯隐格式的混合有限分析法, 根据实测资料对其进行了验证。比较显示, 采用实测资料和经验公式计算到的伶仃洋水域纳潮量与数学模型的计算结果相差在5%以内, 从而证实了数学模型的可靠性。结果表明, 伶仃洋海域的主要纳潮口门为伶仃洋口门, 约占总纳潮量的 87.7%, 通过香港暗士顿水道进出的潮量仅占 12.3%左右, 显示伶仃洋口门为该海域的主要径潮通道, 对该河口的防洪和生态具有重要的作用。
伶仃洋; 纳潮量; 经验公式; 数学模型
随着近 30 a来填海造陆等工程建设, 伶仃洋海域河口岸线及地形条件变化显著, 对该水域的纳潮量影响巨大。纳潮量是一个海湾可以接纳潮水的体积, 是海湾环境评价的重要指标, 对伶仃洋海域的纳潮演变进行分析和研究, 有助于理解伶仃洋海域近些年来的生态环境变化, 并对开展的河口治理提供科学依据。有关河口纳潮量的研究和分析成果较多, 如乔贯宇等[1]采用 ADCP(声学多普勒海流剖面仪)方法对胶州湾口进行走航观测, 得到了胶州湾的纳潮量; 陈红霞等[2]同时采用海图和 ADCP方法计算胶州湾的纳潮, 并进行了比较和分析; 叶海桃等[3]将滩涂和水域分开, 计算了三沙湾的纳潮量和水体交换时间; 吴隆业等[4]采用遥感影像资料得到了海口港的水域面积进而计算了纳潮量的变化; 杨世伦等[5]考虑到河口潮滩被围垦的情况, 改进了传统的纳潮计算公式, 对胶州湾的纳潮量进行了重现计算和分析。
有关伶仃洋河口的纳潮研究成果相对较少, 但与纳潮变化密切相关的河口水动力、水环境及水文地形变化的研究成果很多。如徐峰俊等[6]和陈水森等[7]根据以往研究资料分析了伶仃洋的水动力环境、水域面积、滩槽面积和冲淤变化情况等, 并提出了相应的治理策略。本文将分别通过建立伶仃洋河口二维数学模型及采用经验公式的方法来计算伶仃洋河口水域的纳潮量, 将两种方法相互进行对比验证。水文验证资料采用2007年8月份的大潮和中潮资料以及2001年2月小潮实测资料。在此基础上, 对伶仃洋水域的纳潮特性进行分析和探讨。
1 纳潮量计算方法
通常情况下, 纳潮量是指平均潮差条件下某一海湾可能接纳的海水量, 其计算公式为:

式中P为平均潮差条件下的纳潮量, HΔ为平均潮差, S为平均水域面积(即平均高潮位与平均低潮位面积之均值)。平均高潮位和平均低潮位之差值, 可根据验潮站的多年实测资料求得, 该计算方法简单,计算结果趋于一致。然而, S的计算较为复杂。地形图上一般只标出0 m线(理论最低潮位)和岸线(相当于最大高潮线), 位于两者之间的平均高潮线和平均低潮线需经推算方能得到。
对伶仃洋的纳潮量计算, 此处一方面采用公式(1)进行计算; 另一方面基于建立的珠江河口二维数学模型, 通过在河口口门位置设置特征断面来统计伶仃洋的纳潮量。
2 数学模型及验证
2.1 数学模型
采用的正交曲线坐标系下的二维水深平均水动力数学模型如下:
连续方程:

动量方程:

式中: ξ, η 为曲线坐标系(无量纲); U, V 分别为 ξ, η 方向的垂向平均流速(m/s); ξ为水位(基准面到自由水面的距离, m); Q为源汇项(m3/s); H为总水深(m);,为曲线坐标到直角坐标的变换参数(m);ρ为水体密度(kg/m3); f为柯氏系数(s-1); g为重力加速度(m/s2); vt为紊动黏性系数(m2/s); t为时间(s)。
2.2 数值计算方法及计算水域
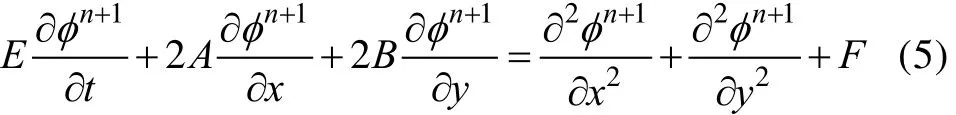
二维潮流数学模型中的偏微分方程可以写为如下统一形式:应用本文提出的纯隐格式的混合有限分析法对该方程进行离散, 离散详细步骤可以参见相关文献[8]。同时此处采用C型网格结合SIMPLER算法用于速度和水位的耦合求解。由于采用曲线规则网格, 计算是沿行或列进行, 因此计算前首先需要对计算区域的复杂边界进行识别, 其相关处理方法以及计算区域存在的浅滩的处理方式可以参见相关文献[9]。
珠江口水域数模计算范围如图 1所示, 东西距离约63 km, 南北距离约145 km。整个计算域包括狮子洋、伶仃洋西东口门、香港水道、伶仃洋外万山群岛等。采用贴体正交曲线网格, 共布网格436个×665个, 最大网格尺寸250 m×140 m, 最小网格尺寸30 m×8 m。
2.3 初始条件和边界条件
流场数值模拟的初始条件为静止状态; 上边界四个河口(虎门、蕉门、洪奇门和横门)给定为实测流量边界, 外海开边界不同时刻的潮位由实测值通过插值方法给定, 流速采用二类边界条件, 即各时刻边界上的流速值赋值为相邻内部网格点上的计算值;岸边界给定为无滑移边界条件。
2.4 露滩处理
计算区域存在浅滩, 由于浅滩在涨潮时淹没,退潮时露出, 对浅滩的处理方式影响到计算的稳定、收敛以及计算结果的精度。此处将 Leendertse等[10]在推出ADI数值模式的同时给出的干湿网格判别准则与河道水流数值模拟中常用的冻结法结合起来,准确有效地处理计算区域的浅滩。其基本原理是:(1)某瞬时任一行(或列)计算完毕, 发现某网格点处总水深H小于设定的最小水深Hmin, 则认为干出, 将该处糙率设为极大值(如 108), 即将该干节点处的流速冻结, 同时该点水位为该点底部高程加上最小水深Hmin; (2)在任一时层计算前, 根据干网格节点周围网格节点水位与该干网格节点水位比较来确定该干网格节点是否被淹没, 若被淹没, 则将其糙率恢复为正常值。
2.5 模型验证
分别选取大、中、小三个潮型对模型进行了验证, 用于潮位验证的有 12个站点, 用于流速和流向验证的有 15个站点, 由于篇幅所限, 此处只给出大潮(2007年8月13日21时至8月14日22时)的部分站点(4个潮位站和4个测流站, 如图1所示)验证曲线, 如图2、图3和图4所示, 其他可详见文献[11]。从模型验证结果来看, 无论是计算的量值还是位相,均与实测值基本吻合, 可真实复演伶仃洋的潮流运动, 证明了本文所用模型的实用性。
3 纳潮量的实测资料分析

图1 计算区域及网格剖分图Fig. 1 Calculation area and grids

图2 潮位验证Fig. 2 Verifications for tidal levels

图3 流速验证Fig. 3 Verifications for tidal velocities

图4 流向验证Fig. 4 Verifications for flowing directions
采用公式(1)来计算伶仃洋纳潮量时, 选取处于伶仃洋正中间的内伶仃岛站、赤湾站和金星门站或淇澳站的实测潮位资料。统计显示包括浅滩在内的珠江口门以内的伶仃洋和狮子洋的总水域面积约为1 900 km2, 由于存在浅滩, 潮位不同时, 浅滩所占面积不同, 导致纳潮水域面积也不一样。表1列出了典型潮位站大、中、小潮型下实测高低潮位和潮差。根据建立的伶仃洋河口数学模型计算了不同高低潮位对应的水域面积和平均纳潮水域面积, 由此得到采用不同站点的潮差计算到的大潮、中潮和小潮的纳潮量。
采用实测结果计算分析显示, 大潮时, 采用内伶仃岛站、赤湾站和金星门站的潮差计算到伶仃洋和狮子洋的总纳潮量分别为 29.70亿, 27.97亿,29.46亿m3, 平均后大潮期的纳潮量为29.04亿m3;中潮时, 采用内伶仃岛站、赤湾站和金星门站的潮差计算到的纳潮量分别为25.40亿, 24.27亿, 26.15亿m3, 平均后中潮的纳潮量为25.27亿m3; 2001年2月小潮时, 采用金星门和赤湾站计算到的纳潮量分别为 18.83亿和 20.02亿 m3, 平均后小潮的纳潮量为19.24亿 m3; 显示大潮纳潮量比中潮纳潮量多 13%,中潮纳潮量比小潮多23.9%。计算显示伶仃洋平均纳潮水域面积是小潮最大, 中潮次之, 大潮最小, 主要是大潮的低潮位太低, 导致浅滩出露面积大, 相应平均纳潮水域面积减小幅度也大的缘故。
4 数值模拟计算纳潮量分析
4.1 纳潮断面布置
根据建立的数学模型, 在珠江河口设置特征观测断面, 统计特征断面上不同时刻的进出潮量, 以此得到该水域在一个潮周期内的纳潮量。为此, 在珠江河口海域分别设置了11个特征潮量观测断面, 分别为伶仃洋口门断面、暗士顿水道断面、金星门断面、内伶仃断面、赤湾断面、深圳湾断面、虎门断面、青州断面、九州断面、西槽断面和铜鼓断面, 如图 1所示。这些特征断面的设置主要考虑两方面的因素, 一方面要保证从数值模拟试验结果中准确无误地提取和统计该断面潮量, 断面的设置都与某一条网格线重合; 另一方面, 根据特征观测断面通过的潮量, 能掌握伶仃洋海域当前的纳潮量及其特性。

表1 纳潮量实测资料计算结果Tab. 1 Calculation results and measured data of tide prisms
4.2 伶仃洋纳潮特性分析
伶仃洋海域属于典型的不规则半日潮, 本文根据建立的珠江河口数学模型对大、中、小潮型的数值模拟计算结果, 统计了 7个主要纳潮观测断面在不同时刻的进出潮量及一个潮周期内的总纳潮量,结果如图 5、表 2、表 3和表 4所示。分析可见:(1)一个潮周期内, 伶仃洋海域在本次大、中、小潮通过珠江河口口门(伶仃洋口门和暗士顿口门的平均进出潮量之和)的平均潮量分别是27.88亿, 24.71亿和 19.53亿 m3, 与采用实测资料和公式(1)计算的纳潮量(表1)比较来看, 两者分别相差–0.77亿, –0.56亿和0.29亿m3, 误差在5%以内, 这一方面验证了采用数学模型和设置特征观测断面计算海域纳潮量的准确性和有效性, 另一方面体现了采用实测资料和公式计算海域纳潮量在平均意义上的有效性; (2)在大、中、小潮期, 通过伶仃洋口门断面和暗士顿水道断面的平均纳潮量分别占该海域总潮量的87.7%和12.3%;可见, 伶仃洋海域的主要纳潮口门为伶仃洋口门,通过暗士顿水道的潮量仅占伶仃洋海域总纳潮量的较小部分; (3)伶仃洋海域为典型不规则半日潮, 大潮期, 通过伶仃洋口门断面的潮量中, 第一次涨潮量(19.83亿m3)大于第一次落潮量(6.82亿m3), 第二次涨潮量(30.91亿 m3)则明显小于第二次落潮量(40.21亿m3); 在中潮和小潮期间也呈现同样的变化规律; 且潮型越大, 该现象越明显; (4)淇澳岛–内伶仃岛间的内伶仃断面是内伶仃洋海域的主要纳潮断面, 由该断面进出的平均潮量约占内伶仃海域总纳潮量的 59.1%, 其次是赤湾断面(内伶仃岛–赤湾),约占总纳潮量的28.8%, 金星门断面最小, 约占总纳潮量的12.1%。大、中、小潮时, 内伶仃海域纳潮占整个伶仃洋海域总纳潮量比例分别是58.2%, 60.3%,62.4%, 内伶仃海域纳潮量的比例随潮差减小呈增加趋势, 平均约为60.3%, 外伶仃海域纳潮量占总纳潮比例约 39.7%, 内伶仃洋海域纳潮量要大于外伶仃海域; (5)本次大、中、小潮型中, 通过虎门口门的纳潮量占整个伶仃洋纳潮量的平均比例为 5.3%, 且纳潮比例随潮差减小略呈增加趋势, 说明此处模拟计算狮子洋的纳潮量占总纳潮量的比例为 5.3%; 深圳湾水域的平均纳潮量分别为 0.57亿, 0.44亿和0.28亿m3, 仅占总纳潮量的1.8%; (6)西槽断面和青州断面进出潮量占伶仃洋总纳潮量的比例平均约为46.6%, 可见伶仃洋口门位置靠近西航道深水区是伶仃洋的主要纳潮通道, 位于浅滩区的九州断面仅占总纳潮量的16.7%左右; (7)铜鼓断面的进出潮量占伶仃洋总纳潮量的比例平均约 12.2%, 显示伶仃洋西槽和东槽通过铜鼓断面水域存在一定程度的潮量交换, 该断面的涨潮量明显大于落潮量, 说明落潮时该部分潮量从暗士顿口门退出。
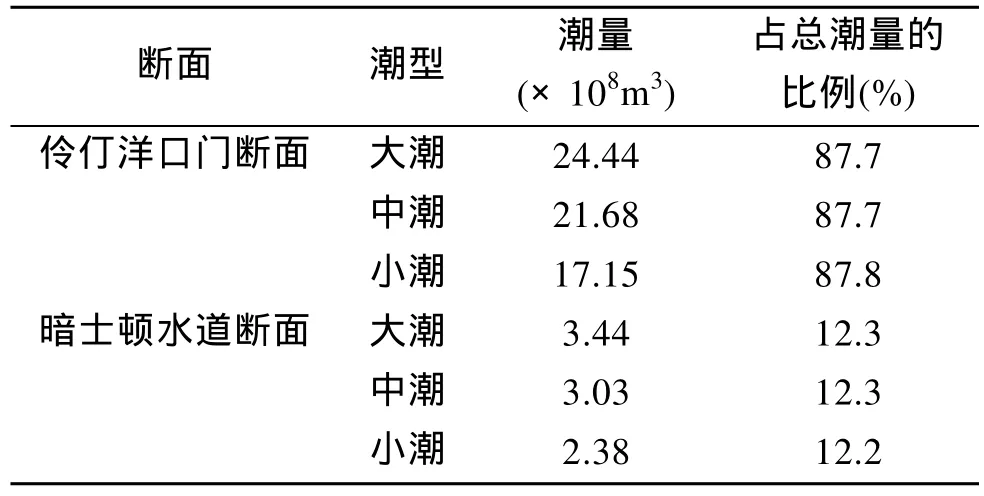
表2 珠江河口口门断面纳潮量计算成果表Tab. 2 Tide prisms in and out of cross sections at the Pearl River mouth by numerical simulations

表3 伶仃洋内各特征口门纳潮量及占总纳潮量的比例Tab. 3 Proportions of tide prisms in and out of cross sections to the totality of the Lingdingyang Bay
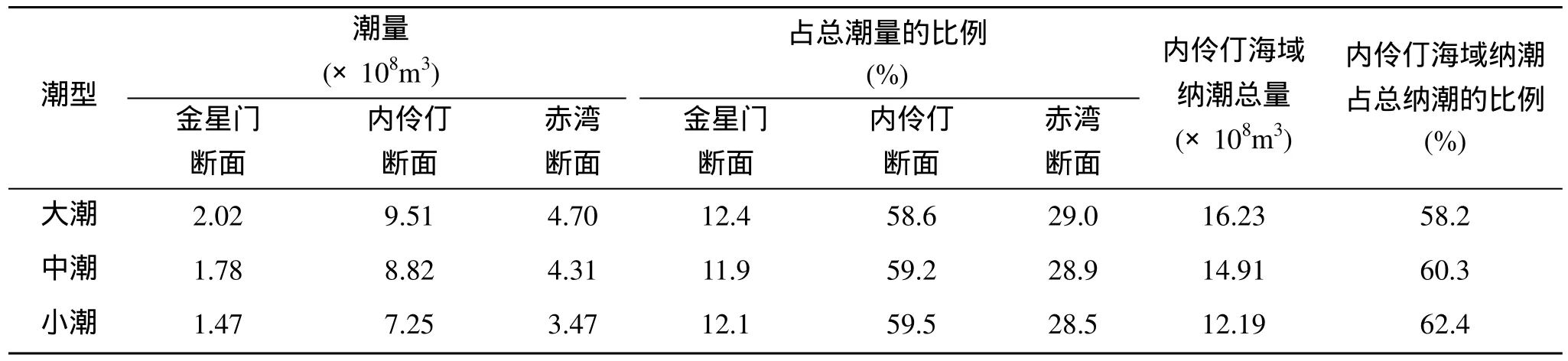
表4 内伶仃海域各口门纳潮统计表Tab. 4 Tide prisms in and out of the cross sections in the inner Lingdingyang Sea

图5 不同潮型下各断面进出潮量速率变化曲线Fig. 5 Tidal prism velocities in and out of cross sections in spring, middle and neap tides
总结以上分析可见, 采用实测资料和数值模拟计算结果统计到的伶仃洋海域纳潮量结果基本一致,确保了潮量计算结果的精度和准确性; 伶仃洋海域的主要纳潮口门为伶仃洋口门(澳门–大濠岛断面),约占总纳潮量的 87.7%, 通过香港暗士顿水道进出的潮量仅占 12.3%左右; 内伶仃海域的纳潮量大于外伶仃海域, 内伶仃海域的纳潮量约占整个伶仃洋海域纳潮量的 60.0%, 外伶仃海域纳潮约占总纳潮量的40.0%。
5 结论
分别采用经验公式和数学模型方法, 对珠江河口伶仃洋水域的纳潮特性进行了计算和分析, 主要结论如下: (1)建立了贴体曲线坐标系下的二维珠江河口水流数学模型, 并采用纯隐格式的混合有限分析法对数学模型进行了离散和求解; 通过将数值模拟结果与实测站点的潮位和流速及流向比较证实了本数学模型和技术方法的有效性和可靠性; (2)采用实测资料和经验公式计算和分析了伶仃洋海域的纳潮量, 显示本次所选大、中、小潮型下, 伶仃洋海域的纳潮量分别为29.04亿, 25.27亿和19.24亿m3; 与数值模拟计算结果相差–0.77亿, –0.56亿和0.29亿m3, 误差在5%以内; (3)伶仃洋海域的主要纳潮口门为伶仃洋口门(澳门–大濠岛断面), 约占总纳潮量的 87.7%, 通过香港暗士顿水道进出的潮量仅占12.3%左右; (4)内伶仃海域的纳潮量大于外伶仃海域, 内伶仃海域的纳潮量约占整个伶仃洋海域纳潮量的 60.0%, 外伶仃海域纳潮约占总纳潮量的40.0%。
[1] 乔贯宇, 华锋, 范斌, 等. 基于 ADCP湾口测流的纳潮量计算[J]. 海洋科学进展, 2008, 26(3): 285-291.
[2] 陈红霞, 华锋, 刘娜, 等. 不同方式的纳潮量计算比较——以胶州湾 2006年秋季小潮为例[J]. 海洋科学进展, 2009, 27(1): 11-15.
[3] 叶海桃, 王义刚, 曹兵. 三沙湾纳潮量及湾内外的水交换[J]. 河海大学学报, 2007, 35(1): 96-98.
[4] 吴隆业, 孙玉星, 王振先. 海口港纳潮量及其变化遥感研究[J]. 海岸工程, 1997, 16(2): 1-5.
[5] 杨世伦, 陈启明, 朱骏, 等.半封闭海湾潮间带部分围垦后纳潮量计算的商榷——以胶州湾为例[J]. 海洋科学, 2003, 27(8):43-47.
[6] 徐峰俊, 朱士康, 王华. 伶仃洋水动力环境分析及治理策略探讨[J]. 人民珠江, 2004, (1): 11-14.
[7] 陈水森, 黎夏, 邹春洋, 等. 20年来珠江口伶仃洋滩槽变化及演变分析[J]. 海洋科学, 2001, 25(6): 52-54.
[8] 李炜. 黏性流体的混合有限分析解法[M].北京: 科学出版社, 2000.
[9] 方神光, 陈纯, 刘涛. 一种纯隐格式在近海潮流数值模拟中的应用[J]. 水道港口, 2008, 29(5): 305-309.
[10] Leendertse J J. A water quality simulation model for well-mixed estuaries and coastal seas, Vol.1, principle of computation[M]. New York: The Rand Corporation,1970.
[11] 方神光. 水流、水质数学模型软件研究和开发——以港珠澳大桥对珠江口水域的纳潮和水体交换的影响研究为例[R]. 广州: 珠江水利科学研究院, 2010.
Characteristics of tidal prism of the Lingdingyang Bay
FANG Shen-guang, CHEN Wen-long, CUI Li-qin
(Pearl River Hydraulic Research Institute of Pearl River Water Resource Committee, Guangzhou 510611, China)
Sep., 20, 2010
the Lingdingyang Bay; tidal prism; empirical formula; mathematical model
Tidal prism characteristics of the Lingdingyang Bay were analyzed on the basis of both empirical formula and a two-dimensional mathematical model under body-fitted curvilinear coordinates. The pure implicit scheme of hybrid finite analytic method was applied to discrete and solute equations. The mathematical model was validated with the measured data. The error between tidal prism calculated by empirical formula using measured data and tidal prism of the Lingdingyang Bay calculated by the mathematical model was less than 5%. The results indicated that the Lingdingyang Bay mouth was the main path of tidal current which accounted for about 87.7% of total tidal prism and Anshidun waterway accounted for about 12.3%. The Lingdingyang Bay mouth was the main channel of flood and tide for the sea and played important role on flood control and estuarine ecosystem.
TV148+.2
A
1000-3096(2012)06-0105-08
2010-09-20;
2012-02-10
国家自然科学基金项目(51109232); 广东省自然科学基金项目(10151061101000001)
方神光(1978-), 男, 湖北监利人, 副研究员, 博士, 从事环境水动力学研究, E-mail: fangshenguang@163.com
(本文编辑:刘珊珊)

