浅薄缺陷的脉冲漏磁信号特征量提取

费骏骉，左宪章，田贵云，张 云，张 韬

（1.军械工程学院 电气工程系，石家庄 050003；2.77159部队，眉山 620010；3.纽卡斯尔大学 电气电子与计算机工程学院，英国）

脉冲漏磁（Pulsed Magnetic Flux Leakage，PMFL）是近年来发展起来的一种新的无损检测技术。由于结合了脉冲涡流检测技术和漏磁检测技术的特点，PMFL 技术在铁磁性材料缺陷的定量评估方面体现出了潜在优势［1－2］。根据文献［3］可知，对于深度无限的平面导体，其涡流密度的分布随着距导体表面的深度呈指数规律衰减。涡流渗入导体内的距离称为透入深度，定义涡流密度衰减到其表面值1／e时的透入深度为标准透入深度，也称为集肤深度。集肤深度与激励频率、导体的电导率和磁导率都有关系，其表达式如下：

式中δ为集肤深度，m；ω为角频率，rad／s；μ为磁导率，H／m；σ为电导率，S／m。

根据傅里叶变换公式，脉冲漏磁检测中的脉冲激励方波信号中包含丰富的频率分量，因此和传统单频交流磁化方式相比，大大提高了激励磁场在试件中的渗透深度；同时，根据式（1），磁场分布由于集肤效应而趋于磁路表面，和静磁场相比，对上下表面的缺陷检测灵敏度更高。

目前国内外学者对脉冲漏磁检测信号中的缺陷特征量研究较多。文献［1］对缺陷处的脉冲漏磁信号做了定性分析，结果显示，和漏磁信号相比，脉冲漏磁信号在时域和频域包含更多缺陷信息。文献［4－5］利用有限元方法对管道上矩形缺陷的检测进行了仿真，定性分析了检测信号的峰值电压与缺陷深度、宽度及传感器提离的关系，结果表明，信号幅值对提离值的变化比较敏感。文献［6－7］用周向矩形缺陷模拟管道腐蚀情况，研究了检测信号峰值时间和缺陷深度以及上下表面位置的关系。

文章将浅薄缺陷作为研究对象，为了提高脉冲漏磁对浅薄缺陷的检测能力，降低提离效应对信号特征分辨率的影响，在分析了脉冲漏磁检测中涡流效应特点的基础上提出一种二次差分方法，分离出在涡流效应的阻尼作用下产生的脉冲漏磁信号涡流分量，并从中提取出了浅薄缺陷深度的新特征量。

1 脉冲漏磁检测中的涡流效应

脉冲漏磁检测铁磁性材料的原理示意图如图1所示。传感器包含U型磁轭、激励线圈和检测探头。脉冲激励信号是具有一定频率和占空比的方波，加载至绕制在磁轭上的激励线圈中，从而在磁路中产生脉冲瞬态磁场，当试件中存在缺陷时，缺陷处的脉冲漏磁场将发生变化，从而改变检测探头感应的瞬态电压，通过分析瞬态电压可获知缺陷情况［8－9］。

图1 脉冲漏磁检测原理示意图

由于脉冲漏磁检测中的激励磁场为瞬态磁场，U型结构的脉冲漏磁传感器在对铁磁性材料进行检测时，被测试件会在激励磁场的作用下感生涡流场。这里的感生涡流可以分成两部分来看，一部分如图2所示，分别以两个磁轭为中心，分布于试件上表面附近；另一部分如图3所示，环绕试件内部的磁路分布［10］。由于铁磁性材料磁导率较高，根据式（1）和麦克斯韦方程，试件中的感生涡流渗透深度很浅，同时感应强度很大。

同时，根据文献［11］，脉冲电磁波在导体介质中传播到t时刻时对应的深度d可依据式（2）得到，其中μr和σ分别是金属导体的相对磁导率和电导率。

可见，脉冲电磁波在导体介质中的传播速度与相对磁导率和电导率的乘积成反比，以铝和钢为例，按铝的相对磁导率μr＝1，电导率σ＝3.4×107S／m，钢的相对磁导率μr＝300，电导率σ＝5×106S／m来计算，脉冲电磁波在铝中的传播速度是钢的44倍，也就是说涡流密度峰值时间在钢中的分辨率是在铝中的44倍，说明在脉冲漏磁检测中，感生涡流密度峰值时间在深度方向上有很强的分辨率。

2 二次差分方法

在运用脉冲漏磁方法对铁磁性材料进行检测时，试件中的涡流效应会对磁路中的磁场变化形成阻尼。当试件中存在缺陷时，缺陷会扰动感生涡流的流动模式，进而影响涡流效应对磁场的阻尼作用。由于特征不同的缺陷对感生涡流的扰动特征不同，涡流效应对磁场的阻尼作用也就不同。因此，在涡流效应的阻尼作用下产生的瞬态磁场涡流分量中应包含缺陷信息。

为了分离出脉冲漏磁信号中的涡流分量，提出一种对脉冲漏磁信号进行二次差分的方法。其基本思想为，假设A和B是两个带缺陷的试件，A为铁磁性材料，B的电导率为0，其它材料属性、大小尺寸和缺陷设置与A相同，用脉冲漏磁传感器对A和B进行检测，在A和B的缺陷上方相同位置分别采集脉冲漏磁信号Bza和Bzb，再在无缺陷位置分别采集参考信号Bzac和Bzbc，可得到差分信号ΔBza＝Bza－Bzac和ΔBzb＝Bzb－Bzbc。显然，ΔBza是在有涡流效应存在的情况下得到的信号，而ΔBzb是在无涡流效应存在的情况下得到的信号，换言之ΔBza中包含涡流分量而ΔBzb中不包含。从理论上讲，ΔBzb－ΔBza就是从脉冲漏磁信号中分离出的涡流分量，它反映了由缺陷扰动引起的涡流效应对磁场阻尼作用的变化量，包含着缺陷信息。在这里，ΔBza也被称为一次差分信号，ΔBzb作为ΔBza进行第二次差分的参考信号，也被称为二次参考信号，而涡流分量ΔBzb－ΔBza是脉冲漏磁信号Bza经过两次差分后得到的，所以称ΔBzb－ΔBza为二次差分信号。

3 二次差分信号中的浅薄缺陷特征量

采用有限元分析软件ANSYS对图4所示的脉冲漏磁检测模型进行计算。为了获得一次差分信号ΔBza和二次参考信号ΔBzb，分别设计了两组尺寸为150mm（长）×100mm（宽）×10mm（高）的被测试件，第一组试件的相对磁导率μr＝300，电导率σ＝5×106S／m，第二组试件的相对磁导率μr＝300，电导率σ＝0，每组包含五个试件，每个试件含一个缺陷，五种缺陷的长度（10mm）和宽度（2mm）相同，深度分别为0.1，0.2，0.3，0.4，0.5mm。

图4 有限元仿真模型

传感器尺寸及坐标方向设置如图5所示，激励线圈由400匝线径为0.3mm的铜线绕制而成，激励电流选择呈指数上升且占空比为50%的方波函数，幅值为0.3A，频率为50Hz。由于脉冲激励信号的时域特点，需对所建模型进行瞬态分析，为了保证计算结果的精度，还需在求解器中设置多个载荷步。由于瞬态计算占用资源大、耗时长，考虑到激励电流波形的对称性，只对激励的正半周期进行计算。

图5 传感器尺寸图

图6显示了一个典型的一次差分信号ΔBza和二次参考信号ΔBzb，以及两者差分得到的二次差分信号。信号ΔBza和ΔBzb趋势相同，都是起始段急剧上升，之后上升速度变慢，而二次差分信号则是先上升后下降。图7所示的是提离值为1mm时在缺陷长度边缘中点获得的信号，经过二次差分处理后的结果。图中，深度从0.1～0.5mm的缺陷，其二次差分信号峰值时间Pt依次出现在279，298，315，331，344μs，深度差为0.1mm时对应的时间差ΔPt依次为19，17，16，13μs。可以看出，在表面缺陷的最小深度差仅为0.1mm的情况下，二次差分信号峰值时间作为缺陷在深度方向上的特征量具有良好的分辨率，这和铁磁性材料中感生涡流的密度峰值时间在深度方向上具有高分辨率的特点一致。

值得注意的是，实际中很难找到电磁属性像试件B一样的材料，也很难用检测手段获取Bzb和Bzbc，进而通过ΔBzb－ΔBza分离出脉冲漏磁信号中的涡流分量。因此考虑寻找能代替ΔBzb的信号。通过对试件B上方采集的脉冲漏磁信号Bzb和参考信号Bzbc进行分析发现，不同位置的Bzb和Bzbc都和激励信号φe成线性关系，进而说明ΔBzb和φe也成线性关系。根据这一特点，考虑通过φ＝k·φe将激励信号进行适当比例的缩放后，用信号φ－ΔBza代替ΔBzb－ΔBza，从而得到在实际中能够应用的二次差分方法。由于感生涡流的存在从整体上对磁路中的磁场起阻尼作用，当激励磁场的幅值稳定后，感生涡流会迅速衰减，阻尼作用也会逐渐消失。理论上如果脉冲宽度够宽，当感生涡流完全消失后，ΔBza和φe的波形应该成线性关系，幅值大小和ΔBzb一样，但在这之前，ΔBza在总体上应该小于ΔBzb。同时，从频域的角度来考虑，方波脉冲激励下的检测信号在各频率成分中都应包含缺陷信息，而信号不同频率成分能量的比例关系，主要是由信号的时域波形而不是幅值大小决定。进而从时域的角度考虑，可以认为缺陷信息应主要包含于信号的波形中，特别是对不同缺陷的识别应主要依赖于不同信号间波形的关系，而不仅仅依赖于幅值的大小。因此这里主要考虑保留信号波形的信息，将脉冲漏磁差分信号ΔBza的峰值与激励信号φe的峰值的比值作为k值，进而求取ΔBzb的近似值φ。

图8是通过应用型二次差分方法对脉冲漏磁信号处理后的结果。图中深度从0.1～0.5mm的缺陷其二次差分信号峰值时间Pt依次出现在270，290，307，323，336μs，深度差为0.1mm 时对应的时间差ΔPt依次为20，17，16，13μs。与理论上的二次差分信号相比，缺陷特征量的分辨率基本没有变化；缺陷深度从0.1～0.5mm每加深0.1mm，信号幅值增加的比例分别为73.1%，34.7%，22.3%，16.3%，在理论算法中为74.4%，34.3%，20.9%，14.4%，幅值大小关系和变化趋势和理论上基本一致，表明二次差分方法具有在实际检测中的可行性。

图8 应用型二次差分信号

4 试验结果分析

建立脉冲漏磁检测系统，对激励线圈施加频率为50Hz，幅值为0.5A，占空比为50%的脉冲电流方波，分别对人工加工的长度（8mm）和宽度（1 mm）相同，深度分别为0.1，0.2，0.3，0.4，0.5mm的表面缺陷进行检测。用霍尔元件检测探头在无提离的情况下采集缺陷长度边缘中点的脉冲漏磁信号，在无缺陷处获得参考信号，一次差分信号的平均幅值为938.79mV，缺陷深度差为0.1mm时的平均幅值差为128.84mV，二次差分信号峰值时间平均为156.7μs，缺陷深度差为0.1mm时的平均时间差为12.8μs。

在不同提离值（1～5mm）下通过对信号进行一次和二次差分处理得到的数据结果如图9和表1。

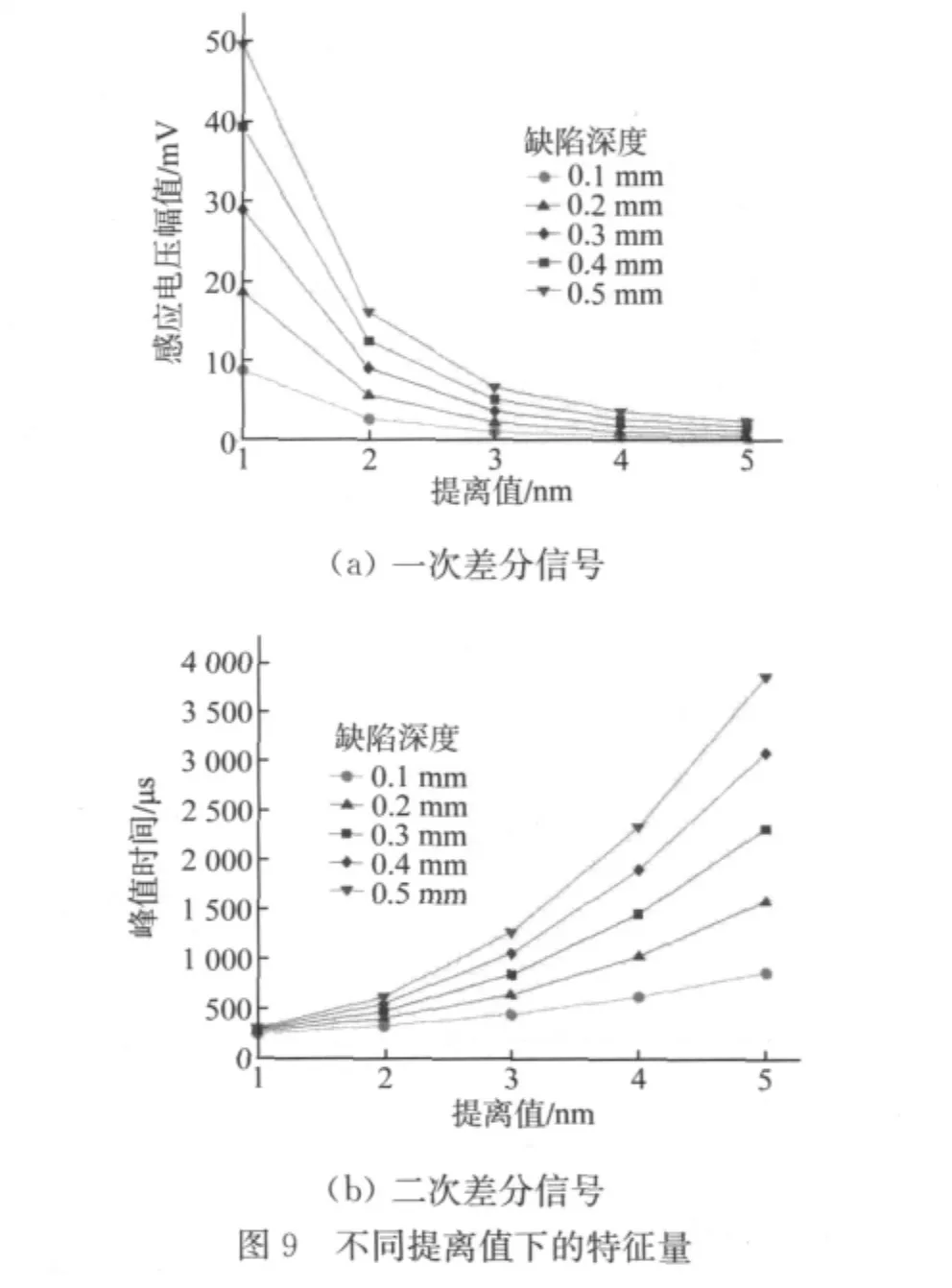
从图9可以看出，一次差分信号幅值A随着提离值的增加而衰减，二次差分信号峰值时间Pt随着提离值的增加而延长，表1和表2反映了两个特征量的分辨率随着检测探头提离值的增加有着相反的变化趋势，检测探头提离值为5mm时的一次差分信号幅值的分辨率比在提离值为1mm时下降了95%，而二次差分信号峰值时间的分辨率则提高了3000%；同时，提离值为1mm时的一次差分信号平均幅值为36.14mV，平均幅值差为10.22mV，和无提离值下的对应值相比分别下降了96.15%和92.07%，说明一次差分信号的幅值对提离相当敏感，特别是检测探头从0mm提离到1mm的过程中，特征量的大小和分辨率衰减速度很快。

表1 一次差分信号幅值的分辨率

表2 二次差分信号峰值时间的分辨率

5 结论

通过提出的二次差分方法，分离出了在涡流效应的阻尼作用下产生的脉冲漏磁检测信号中的涡流分量，即二次差分信号，并根据铁磁性材料中涡流效应的特点，从二次差分信号中提取了浅薄缺陷特征量——二次差分信号峰值时间Pt。试验结果表明，脉冲漏磁差分信号的幅值对检测探头的提离比较敏感，并且随着提离值的增加，其分辨率很快降低，而新的特征量在检测探头提离的情况下仍然具有较高分辨率，并且分辨率随着提离值的增加而提高。这为脉冲漏磁检测浅薄缺陷提供了一种新的有效方法。

［1］Wilson John W，Tian Gui Yun.Pulsed electromagnetic methods for defect detection and characterisation［J］.NDT＆E International，2007，40（4）：275－283.

［2］Sophian A，Tian G Y，Zairi S.Pulsed magnetic flux leakage techniques for crack detection and characterization［J］.Sendors and Actuators A，2006，125（2）：186－191.

［3］Sophian Ali，Tian Gui Yun，Taylor David，et al.A feature extraction technique based on principal component analysis for pulsed Eddy current NDT ［J］.NDT＆E International，2003，36（1）：37－41.

［4］唐莺，罗飞路，潘孟春，等.脉冲漏磁检测的三维场特征分析及缺陷分类识别［J］.仪器仪表学报，2009，30（12）：2506－2510.

［5］唐莺，罗飞路，潘孟春，等.脉冲漏磁检测管道技术的有限元分析［J］.无损检测，2009，31（7）：513－516.

［6］唐莺，潘孟春，罗飞路，等.管道腐蚀检测中的脉冲漏磁检测技术［J］.计算机测量与控制，2010，18（1）：38－39.

［7］王韫江，王晓锋，丁克勤.基于脉冲漏磁理论的管道腐蚀缺陷宽度定量技术［J］.测试技术学报，2009，23（5）：390－395.

［8］Chen Tian Lu，Tian Gui Yun，Sophian Ali，et al.Feature ext raction and selection for defect classification of pulsed eddy current NDT［J］.NDT＆E International，2008，41（6）：467－ 476.

［9］Huang Zuoying，Que Peiwen，Chen Liang.3DFEM analysis in mengnetic flux leakage method ［J］.NDT＆E International，2006，39（1）：61－66.

［10］Javier García－Martín， Jaime Gómez－Gil， Ernesto Vázquez－Sánchez.Review non－destructive techniques based on eddy current testing［J］.Sensors，2011，11（3）：2525－2565.

［11］Blitz J，Peat T S.The application of multi－frequency eddy currents to testing ferromagnetic metals［J］.NDT International，1981，14（1）：15－17.