基于谐波特征和GA－SVM的刀具状态监测*

陈泽宇

（广州铁路职业技术学院，广东广州 510430）

在机械自动化加工中，刀具状态监测有利于提高机械的加工质量及加工效率，降低加工成本，因此监测刀具状态是现代化加工技术的重要课题［1］。目前，监测刀具状态的常用方法有直接监测和间接监测，直接监测主要用于监测刀具切削力参数;间接监测用于监测加工中的振动、声发射（AE）、电动机电压电流等参数。文献［2］中研究表明，在金属切削过程中，刀具的摩擦、切削和断裂时会产生机械波，此即为AE信号。AE信号包含加工过程丰富信息，是典型的非平稳信号。采用AE信号作为监测信号，有灵敏度高，响应速度快等优点，是近年发展起来的检测方法，已经应用于多种监测上。

目前，谐波特征实际上指的是信号中各次谐波的幅值和相位，通常采用傅里叶变换及其改进算法。然而AE信号为非平稳信号，傅里叶（Fourier）变换总是假设信号是周期性的，所以通过傅里叶变换进行谐波特征监测是不准确的。与Fourier变换相比，小波变换是一个时频的局域变换，能通过伸缩和平移等功能从信号获得细化的信息。故本文提出了基于小波变换提取谐波特征和GA－SVM的方法，进行刀具状态监测，运用小波变换提取谐波特征，采用遗传算法优化支持向量机的参数选取，来建立刀具状态监测模型。

1 谐波特征

1.1 小波变换

设ψ（t）∈L2（R），L2（R）表示平方可积的实数空间，即能量有限的信号，其傅立叶变换为φ（ω）［3］。当φ（ω）满足相容性条件时:

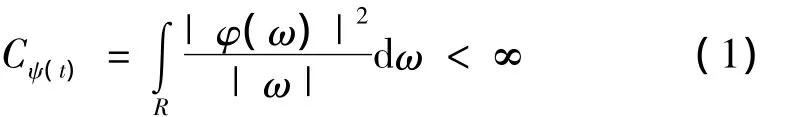
称ψ（t）为一个基函数。对于连续的情况，小波函数为

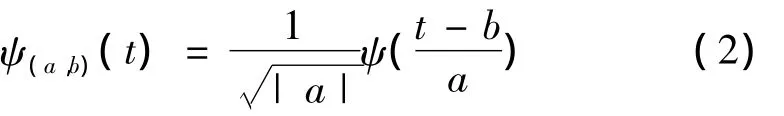
满足条件a＞0且a，b∈R。其中变量a为伸缩因子，反映某一个特定基函数的尺度;b为平移因子，表示基函数沿坐标轴X的平移。对于信号f（n），其小波变换为

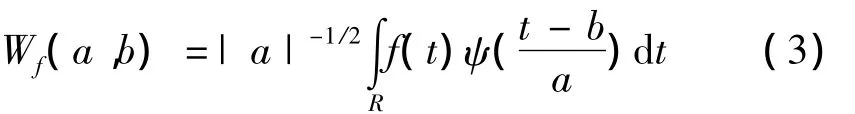
式中，Wf（j，k）为小波系数。随着尺度j的增大，相互正交的小波基的空间分辨率愈高，从而提高时频分辨率。其逆变换为

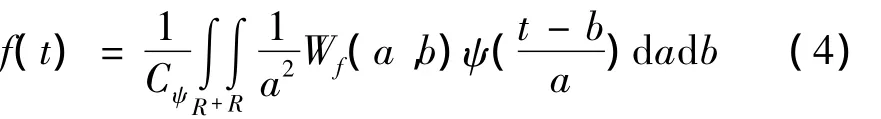
1.2 谐波特征检测

谐波的定义是信号进行傅里叶变换或小波变换，得到与基函数频率相同的分量，这部分的分量被称为信号在该次频率上的谐波。理论上，一个信号可以有无数的谐波。谐波频率与基函数频率的比值成为谐波的次数。把信号分解为不同次数的谐波，此即为信号的谐波特征［4］。

基于小波变换的谐波特征检测一般分为3步:首先对信号进行小波变换，把时域信号转换到频域，分解到各次谐波的频带中。其次按需要设定阈值函数，对分解后的小波系数进行处理，如只想获得该次谐波的基频部分，即可令高于该次谐波的高频系数全部为零。最后把处理后的小波系数进行重构叠加，得到相应次数的谐波的时域信号［5］。

2 GA－SVM方法

2.1 遗传算法

遗传算法（Genetic Algorithm）是一类借鉴生物界的进化规律（适者生存，优胜劣汰遗传机制）演化而来的随机化搜索方法。它是一种高度并行、随机和自适应的优化算法，它将问题的求解表示成“个体”的适者生存过程，通过“个体”的不断进化，包括复制、交叉、变异等操作，最终收敛到“最适应环境”的个体，从而求得问题的最优解或满意解［6］。本文根据作者实验研究所得，种群规模N=100，交叉概率Pc=0.85，变异概率Pm=0.02，迭代次数n=50。

2.2 支持向量机（SVM）

再构造Lagrange函数求解，根据Wolfe对偶规则转化为凸二次规划问题:

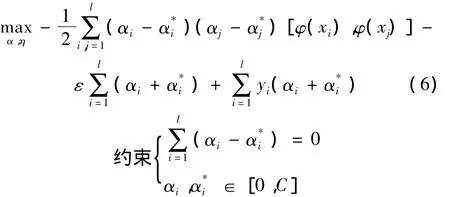
整理为标准形式，可得最优解:

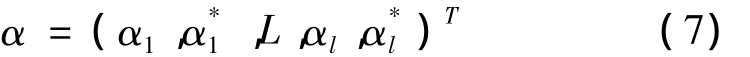
根据最优解构造决策函数:

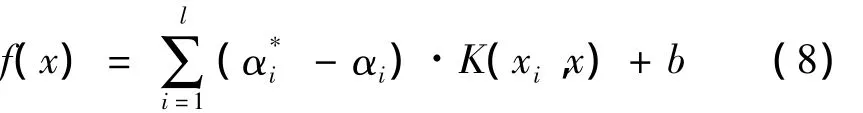
此即支持向量回归机的决策函数。根据决策函数能对样本集之外的新输入精确估计出相应的输出。文中选取应用最广泛的高斯径向基核函数。

2.3 GA－SVM（遗传－支持向量机）

在 SVM分类估计中，选择合适的参数c、ε有助提高分类的准确度。其中参数c作为惩罚因子，决定模型的复杂程度和拟合偏差的惩罚程度。c值过大或过小都会减弱系统的泛化能力;参数ε表示系统对分类函数在样本数据上误差的期望，其值影响了构造分类函数的支持矢量数目。ε值过小，分类估计准确度虽然高，但支持矢量数量多，会导致过学习现象［7］。根据GA遗传算法的寻优计算方法，不断优化支持向量机的参数选择，直到适应度函数最小为止，然后利用支持向量机建立最优结构误差的刀具状态监测模型，然后预测刀具状态。算法的主要步骤描述如下:

step1:初始化种群代数t=0。

step2:由于选择的ε－SVM支持向量机，高斯径向基函数作为核函数，那么需要优化的参数为惩罚参数c以及不敏感系数ε，用实数编码成的个体表示需优化的参数组成，随机生成初始化种群p（t），其种群大小为100。

step3:把每组参数代入ε－SVM支持向量机，用训练样本对其进行训练，用交叉验证误差作为参数优化准则，计算每组参数的适应值F（t），即组内的最小均方误差。

step4:若种群中最优个体所对应的适应度值满足中止条件，则转到步骤step7。

Step5:基于排序的适应度分派原则确定第i个个体被选择的概率，进行交叉运算，产生新的个体。

Step6:采用变异算子，个体按一定概率进行变异操作之后转到step3。

Step7:选择得到的最优的c、ε进行预测。

3 基于谐波特征和GA－SVM的刀具状态监测

通过对信号进行小波变换，把信号分解到不同次数相互独立的频带内，然后计算各频段内信号的谐波特征，它们包含了大量源信号的信息，把它们作为表征刀具状态的特征信息，识别出刀具状态，从而完成刀具状态的检测。具体流程如图1所示。

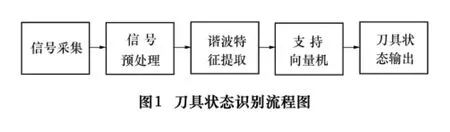
（1）首先对采集到的AE信号进行预处理，在尽量保留其特征情况下过滤掉噪声信息。

（2）小波层数的选择对信号的特征有重要的影响。小波层数选择过少，识别结果容易出错。小波层数选择越大，计算速度越慢，影响程序实时性。经过试验，决定选择5层小波变换。

（3）对分解后的信号进行谐波特征提取，输入到GA－SVM中，进行训练，并寻找最佳的SVM参数。

（4）故障结果输出。

4 实验分析与结果

4.1 试验过程

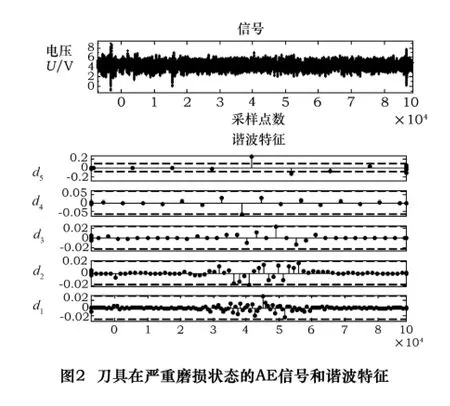
试验是在X6325机床上进行的，工件材料为45钢，无切削液润滑。电动机主轴转速300 r/min，进给速度30 mm/min，切削深度3 mm，刀具直径16 mm。采样频率:10 k;采样点数:100 000。在本研究中，把刀具状态分为新刀具，轻度磨损，中度磨损，严重磨损几种状态。提取相应状态的AE信号的谐波特征，作为此状态的表征，输入到GA－SVM，建立起刀具状态与谐波特征的关系。严重磨损状态的AE信号和其谐波特征如图2所示。

4.2 实验分析

通过实验对刀具的状态进行测量，每5 min进行一次数据采集，总共采集了50组数据。50组数据中分为26组的训练数据和24组的测试数据，训练数据用于建立刀具状态模型，测试数据用于测试模型的准确度。

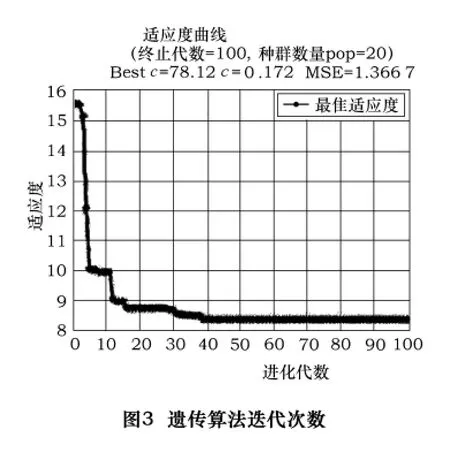
为了体现GA－SVM建立刀具状态模型的能力，用测试数据测试GA－SVM所建立模型的正确性。图3为GA遗传算法的c、ε两个参数迭代过程与最优值。从图中可以看到只需要40次迭代，c、ε两个参数得到最优值78.12和0.172，体现了遗传算法良好的寻优能力。

从表1的识别结果可以看出，用经过GA优化的SVM支持向量机控制参数，分类的正确率高达91.7%，满足正常使用需要。因此用GA－SVM建立的刀具状态模型是有效的。

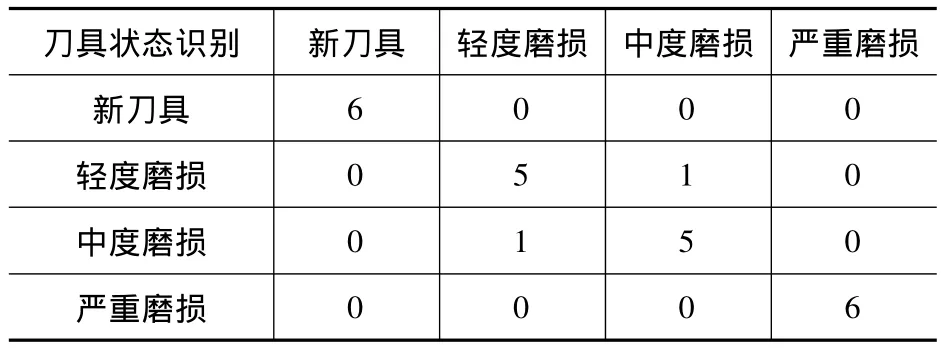
表1 识别结果

5 结语

通过小波变换提取刀具状态信号的谐波特征，作为向量输入到支持向量机，经过GA优化支持向量机的参数，建立了基于GA－SVM的刀具状态模型。经试验证明，刀具状态模型能较好的识别刀具所处状态，其正确率高达91.7%，具有实际工程应用意义。

［1］曾祥超，陈捷.数控机床刀具磨损监测实验数据处理方法研究［J］.机械设计与制造，2009（1）:213－215.

［2］陈新全，李西南，邓敏.金属切削过程中的声发射现象及其研究的意义［J］.长沙电力学院学报，2001，16（1）:75 －76.

［3］崔锦泰.小波分析导论［M］.西安:西安交通大学出版社，1995.

［4］刘争艳，郑恩让，马令坤.基于Matlab的非平稳谐波检测方法仿真研究［J］.化工自动化及仪表，2011，38（1）:69 －71.

［5］张伟.基于变换的谐波检测方法［J］.电力学报，2006，21（1）:21－22.

［6］Schölkopf B，Smola A，Williamson R，et al.New support vector algorithms.NeuroColt2－TR［O/OL］.1998，http://eiteseer.nj.nee.eom/276248.html

［7］郑春红，焦李成，丁爱玲.基于启发式遗传算法的SVM模型自动选择［J］.控制理论与应用，2006.23（2）:187－192.