利用寻位信息的自由曲面在线测量路径规划方法*
邵 伟 郭俊杰
(①西安理工大学,陕西西安710048;②西安交通大学,陕西 西安 710049)
随着航天、航空、造船、汽车等工业的飞速发展,使得自由曲面零件在现代工业中得到了越来越广泛的应用,并且对产品性能、外形等方面的要求越来越高,而对该类工件的曲面建模、数控加工和产品表面质量评定都离不开对自由曲面工件几何形状的测量。其测量精度和效率直接影响到后续处理的质量和效率[1]。为了有效地实现对自由曲面工件的在线测量,就有必要对其进行合理的测量路径规划。测量路径规划是确定测头在测量空间的运动轨迹,即工件上测量点的分布及其测量顺序。测量时一般以面作为最小的测量单位,要求测量完一个面后,才能进行下一个面的测量。测量路径规划的好坏直接影响着测量效率和重构曲面的精度。测点数目的多少受到被测物体尺寸大小、检测公差的精度要求和测量机测量精度大小的综合影响。被测物尺寸大时,应进行多测点测量,尺寸小时则可进行少测点测量;测量的精度要求高时,测量的点数就应该多,反之则少;测量机的测量精度高时,测量相同物体的测点的数目可以少,精度低时就要多。在上述3项一定的情况下,就要对测量点的分布进行研究,使得测量点分布的疏密尽可能地随曲面曲率的变化而变化,同时减小测量机自身误差的影响,使测量结果尽可能地反映工件的实际形状,从而在满足精度要求的前提下使测点的数目尽可能的少,满足在线测量高效率的要求[2-6]。
已知CAD模型的大型曲面测量规划方法是在设计基准坐标系下根据加工精度要求确定测点数和测点分布,以及对应理论模型上的点,由这些点指导测量机进行测量,然后对加工机床进行相应的工艺指导,这就涉及到设计坐标系、测量坐标系、加工坐标的统一,因此在测量路径规划中如何实现设计坐标系、测量坐标系、加工坐标的统一对测量轨迹和加工轨迹的控制至关重要[7-8]。本文提出了一种基于工件寻位的方法,建立坐标系之间的相互关系实现坐标系的统一,其原理就是通过对工件上的特征点的测量来找出测量坐标系相对设计坐标系和加工坐标的相对位置关系,保证测量过程中测头的运动与工件的CAD模型规划轨迹一致。因此本文采用一种基于曲面工件自动寻位的坐标系统一原则和测点布置于一体的测量路径规划方法。下面首先介绍基于曲面工件自动寻位信息的坐标系关系的建立。
1 基于自动寻位信息的坐标系关系的建立
坐标系关系的建立就是要确定设计坐标系、测量坐标系、加工坐标系的相互转换关系,即转换矩阵的求解,因此,建立曲面测量坐标系与设计坐标系和加工坐标系之间的变换关系成为转换矩阵的求解。针对CAD模型己知的待测大型曲面工件,可根据预先测量获取的工件表面上少数测点的信息,通过一定的计算将其与CAD模型上对应的点对齐,快速准确地求解出工件的实际状态(工件在测量机上的位置与姿态),即求解出测量坐标系和设计坐标系之间的真实关系。一般工件测量坐标系和设计坐标系之间的关系可用齐次变换矩阵T表示为
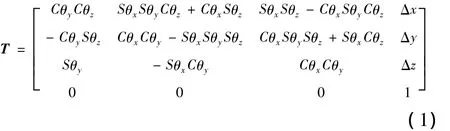
式中:Δx、Δy、Δz为测量坐标系原点相对于设计坐标系原点的平移量;θx、θy、θz分别为测量坐标系绕设计坐标系x、y、z轴的旋转角度;S和C分别是sin和cos的缩写。
由于直接快速精确求解T是比较困难的,为此本文采用如下的方法[9-10]来对模型已知的待测大型工件进行寻位信息提取。该方法具体步骤可描述如下:
(1)初始化——使变换矩阵T0为

其中(xc,yc,zc)为初始测点的质心;并且初始化与测点(i=l,2,…,n;j=1,2,…,m)对应的曲面上的理论点(i=l,2,…,n;j=1,2,…,m)。
(2)计算测点Pij与工件理论曲面间的偏差
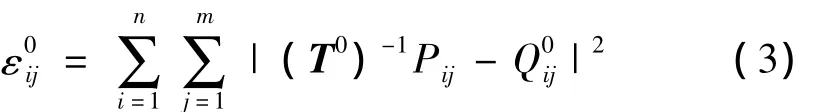
(3)置k=k+l;
(4)确定测点Pij对应的曲面上的理论点
由于测量坐标系的测点相对工件理论曲面间距离的平方为
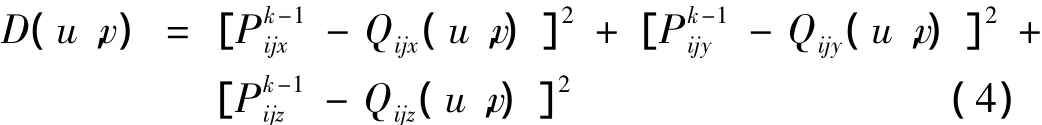
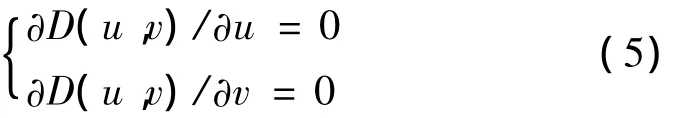
解方程组(5)求出所对应的参变量u、v的取值,最后将u、v之值代入坐标函数表达式,即可求出的坐标值;
(1)进行变换矩阵T更新得到Tk;
(2)求取变换后的测点:

(3)计算与工件理论曲面间的偏差
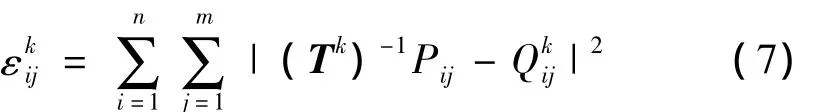
2 基于寻位信息的测量路径规划算法
实现曲面工件寻位测量的关键,是按所获得的工件寻位信息对测量过程进行位姿自适应控制。下面提出一种对已知曲面进行测量的基于寻位信息的路径轨划方法。下面介绍算法的具体实现过程。
2.1 曲面工件的测点生成算法
如果对待测曲面工件的整个几何形状自适应地进行测点布置,将使得计算的工作量相当大,在一定的精度条件下也完全没必要。一种合理的解决办法就是首先根据给定的精度要求,在曲面上自适应生成检测方向上的测量曲线,在避免漏检的前提下尽可能减少测量曲线的数目;然后对每一条测量曲线按等步距进行测点布置以生成曲面工件的测点。其中曲面工件的测量曲线自适应生成就是根据待测曲面的具体几何形状自适应地进行测量曲线的布置,使测量曲线分布的疏密随曲面曲率变化而变化,从而在满足精度要求的前提下使测量曲线的数目尽可能地少,以提高测量的效率。如图1所示,对应于一定精度要求的测量曲线生成过程如下:
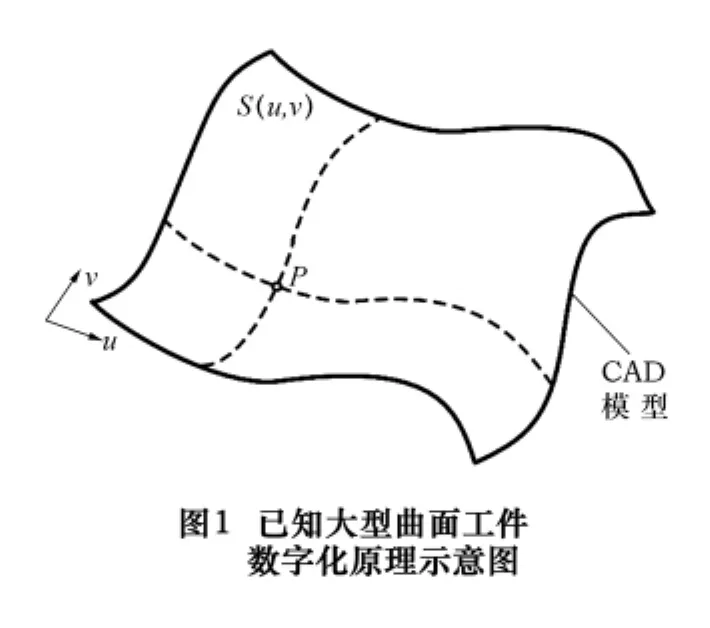
步骤1:检测方向上测量曲线的分布。对于曲面:
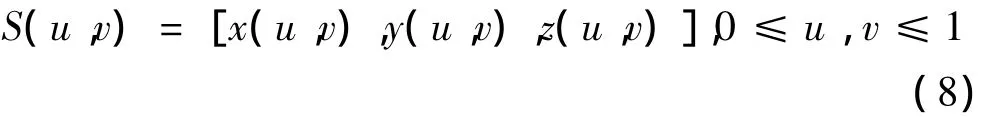
假设参数u方向(或v方向)为其检测方向,并且沿该方向分布n条测量曲线,首先根据扫描间距用等参数方法进行曲面离散(如图1所示),得到各离散型值点Sij=S(ui,vj)(i=l,2,…,r;j=1,2,…,l)。接着,将该离散的曲面按u方向(或v方向)划分成m个离散小曲面,m一般应等于1/5~1/2倍的测量曲线数n。
接着,对每个离散小曲面中各点进行曲率数值的计算。根据欧拉公式,设{e1,e2}是曲面在任一P点的两个彼此正交的主方向单位向量,对应的主曲率为k1、k2,则在P点沿任意一个单位切向量e=e1cosθ+e2sinθ的法曲率为
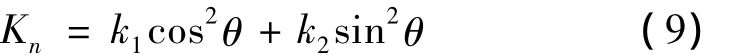
从式(9)不难看出,主方向正是法曲率取极值的方向,而主曲率正好是法曲率极值,即如果k1≥k2,则在曲面上在该点沿任意一个切方向的法曲率满足不等式

在实际应用中,取曲面上P点的绝对曲率
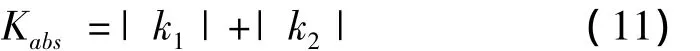
反映曲面上该点的弯曲程度。其中,主曲率k1、k2分别为曲面在一点处的最小、最大曲率。进而通过式(11)可计算出各离散小曲面上各点的曲率测度及其最大最小值。
然后,对每个小曲面采用均匀分布的方法进行测量曲线的分布,分布曲线数ni为
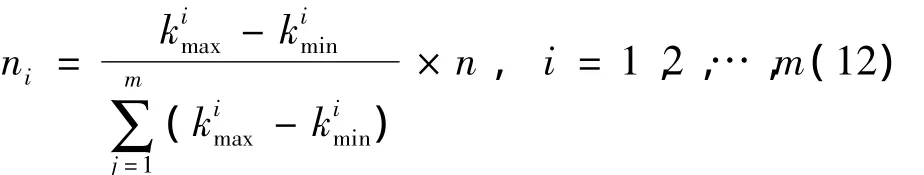
到此,就完成了沿曲面u参数方向(或v方向)n条测量曲线的分布,并将这n条测量曲线作为当前测量曲线集C(n)。
步骤2:由上面确定的n条测量曲线重构CAD模型得到一个替代曲面模型S*。
步骤3:计算曲面模型S*与CAD模型之间的偏差Δ。设ε为测量精度和工序能力共同确定的精度要求,如果

不成立,并且n<N(N为预先指定的正数),则令n=n+1,重复上述过程直至式(13)成立。于是可取C=C(n),由该方法所生成的测量曲线集可以满足对曲面检测测量曲线数目和自适应分布的要求,以便对曲面的形状误差做出准确评定。
2.2 几何信息变换和测量路径的生成
为实现对模型已知的大型曲面工件进行测量,需将待测曲面工件的有关几何信息从设计坐标系变换到测量坐标系。因此,在求得齐次变换矩阵T后,可用T-1对由曲面CAD模型生成的测点数据Qij进行变换,即将CAD模型面的测点变换到测量坐标系中,其表达式为

遍历上述测点数据即可得到的曲面测量路径。
3 仿真与实验
为了验证上述算法的有效性,进行了多次仿真实验。仿真实验之一所用工件的CAD曲面轮廓如图2所示。在一定的精度要求下,利用测量曲线自适应布置算法进行测量曲线自适应分布的结果如图3所示。由图中不难发现测量曲线的分布在曲面曲率大的地方分布得密,而曲率小的地方分布得疏。


对于该工件如按常规方法进行测量,则由于定位不准,使得工件的实际测点与理论测点产生较大的误差,此时测量坐标系相对于设计坐标系的位移和旋转量如表1第二列所示。为消除这种误差,采用寻位控制方法对测量过程进行控制。为此先在工件表面上确定一定数量的测量点(本次实验为10个),并取得这些点的坐标值,将这些测点的数据输入控制计算机,运行该机中的工件定位控制软件,经计算出被定位工件的状态估计值即寻位计算值如表1最后一列所示。
用所求得齐次变换矩阵T后,将工件曲面的自适应测点从设计坐标系变换到测量坐标系,使设计坐标系和测量坐标系趋于一致,此时最大误差为0.008 5 mm。这说明该寻位测量方法具有较高的精度,可以满足曲面工件的测量要求。

表1 工件状态
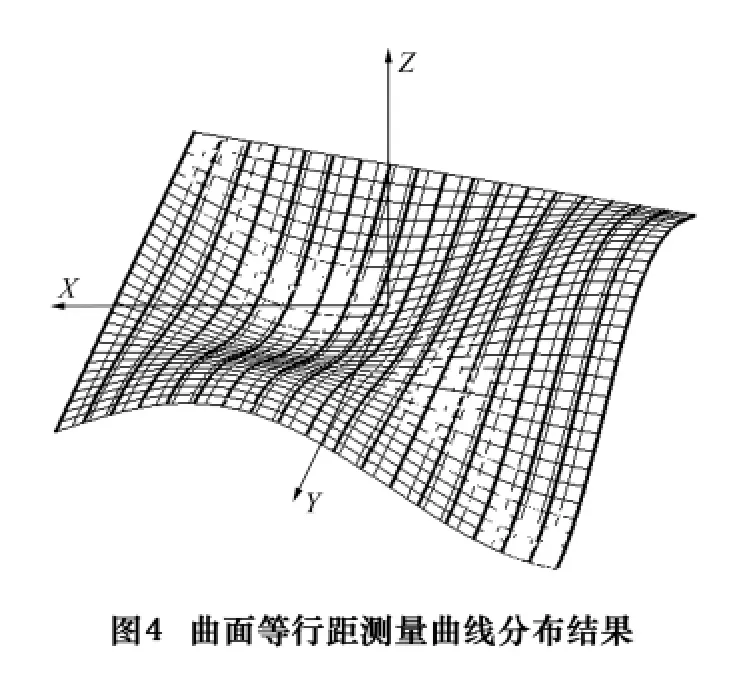
图4为以自适应采样路径规划得到的最小测量曲线行间距(5.236 1 mm)进行等行距测量曲线布置的结果,共有19条测量曲线。由此可见,和本文采用的测量路径规划方法相比,在相同的测量效果下,本文采用的测量路径规划得到的测量曲线数显著减少,可以较好地提高采样效率。
图5为以自适应采样路径规划得到的某工件测量曲线布置的结果和实际测量曲面的误差分布图,其结果和实际基本相符。由此可见,本文采用的测量路径规划方法在相同的测量效果下,可以较好地提高采样效率。

4 结语
提出了一种基于寻位信息的大型曲面工件的设计坐标系、测量坐标系、加工坐标的统一方法,在此基础上实现测量路径规划,实现测量过程中对测点的布置。该方法根据待测曲面上相邻子曲面内测点的平均曲率为判据来进行测量曲线的自适应分布,可以保证测量曲线分布的疏密随曲面曲率变化而变化,以提高测量的效率;接着对每一条测量曲线按等步距进行测点布置以生成曲面工件的测点。然后基于寻位信息,将测点从设计坐标系变换到测量坐标系。仿正和实例表明,上述方法具有算法简洁、采样精度容易控制的特点,在相同采样精度下可显著提高在线测量效率,满足在线测量高效率的要求,有效提高加工质量。
[1]裘祖荣,石照耀,李岩.精密测试技术展望[J].中国机械工程,2010,46(14):1-11.
[2]靳宣强,姜秀丽,胡祯,等.浅析数控机床在线检测技术[J].现代制造技术与装备,2009(3):40-42.
[3]Seokbae S,Seungman K,Kwan H L.Path planning of multi-patched freeform surfaces for laser scaning[J].Int.J.Adv.Manuf.Technol.,vol.224,pp.424 -435,2003.
[4]赵吉宾,刘伟军,孙玉文,等.自由曲面测量点云数据的建模方法研究[J].仪器仪表学报,2006,27(19):1044 -1047.
[5]刘强,李冬茹.国产数控机床及其关键技术发展及展望[J].航空制造技术,2010(10):26-30.
[6]赵振宇,张萌,周后明.最短路优化的复杂型腔刀具轨迹规划算法[J].制造技术与机床,2009(1):39 -42.
[7]石为人,王楷.基于Floyd算法的移动机器人最短路径规划研究[J].仪器仪表学报,2009,30(10):2088 -2092.
[8]梁义,陈建军,陈立岗,等.几何自适应参数曲面网格生成[J].计算机辅助设计与图形学学报,2010,22(2):327-335.
[9]纪小刚,龚光荣.三坐标测量机中基于遗传算法的多特征测量路径规划研究[J].兵工学报,2005,26(3):392 -396.
[10]徐金亭,孙玉文,刘伟军.复杂曲面加工检测中的精确定位方法[J].中国机械工程,2007,43(6):175 -179.

