初始残余应力对铝合金7475板件变形的解析法研究*

林爱琴 郑敏利 樊春光 顾 岩

（哈尔滨理工大学机械动力工程学院，黑龙江哈尔滨 150080）

航空铝合金7475板材主要应用在航空发动机典型板件上，这种材料具有高强度高塑性特点，在实际加工中易引起变形，导致加工精度超差，降低成品率。国内外对工件变形成因有所研究。如Nervi.Sebastian建立了毛坯初始残余应力引起加工变形的数学预测模型，指出零件的最终变形情况与毛坯初始应力的分布状态和形状密切相关［1］。Keith A.Young采用数值模拟与铣削相结合的方法研究了铣削加工引入的残余应力对加工变形的影响，指出加工引入的残余应力与变形与刀尖圆弧半径和切削刃钝圆半径密切相关［2］。黄志刚等人［3］研究了毛坯初始残余应力释放以及多因素耦合对工件加工变形规律的影响，对不同隔框加工顺序进行了分析，确定了工件变形最小的隔框加工顺序。郭魂等人预测了航空框类薄壁件加工过程中的变形，并分析了装夹应力、残余应力对工件变形的影响［4－5］。王秋成利用解析法研究依次剥层时初始残余应力对铝合金7075板材工件变形的影响［6］。根据上述研究表明，初始残余应力是影响工件整体变形的主要因素，大多通过有限元和解析方法依次均匀剥层来分析每剥一层后残余应力释放引起工件变形及释放后残余应力重新分布状态。但是对于一些结构对称零件，通常需要正反面加工的。所以本文根据实际需要研究单面和正反面反复加工两种情况下残余应力的变化及对工件变形的影响，并进行对比分析。

1 单面剥层时残余应力对工件变形影响分析

图1为预拉伸处理的铝合金7475矩形板，根据实际测量的此板材的初始残余应力分布规律及理论计算方便进行如下假设:

（1）初始残余应力在平行于板厚的中间面的任一平面内均匀分布且沿板厚方向对称分布。初始残余应力是自平衡力，在垂直于应力方向的截面内，合力与合力矩都为零，即:

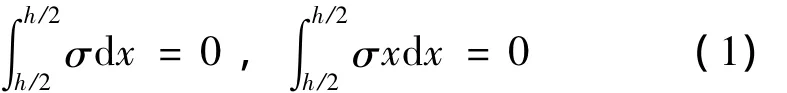
式中:σ为每层的残余应力;h为板厚。

（2）材料具有各向同性，在剥层材料的加工工艺过程中，假设没有切削力、热等其他因素产生的新残余应力场。

（3）将板厚均匀等分，每次去除材料的厚度相等。

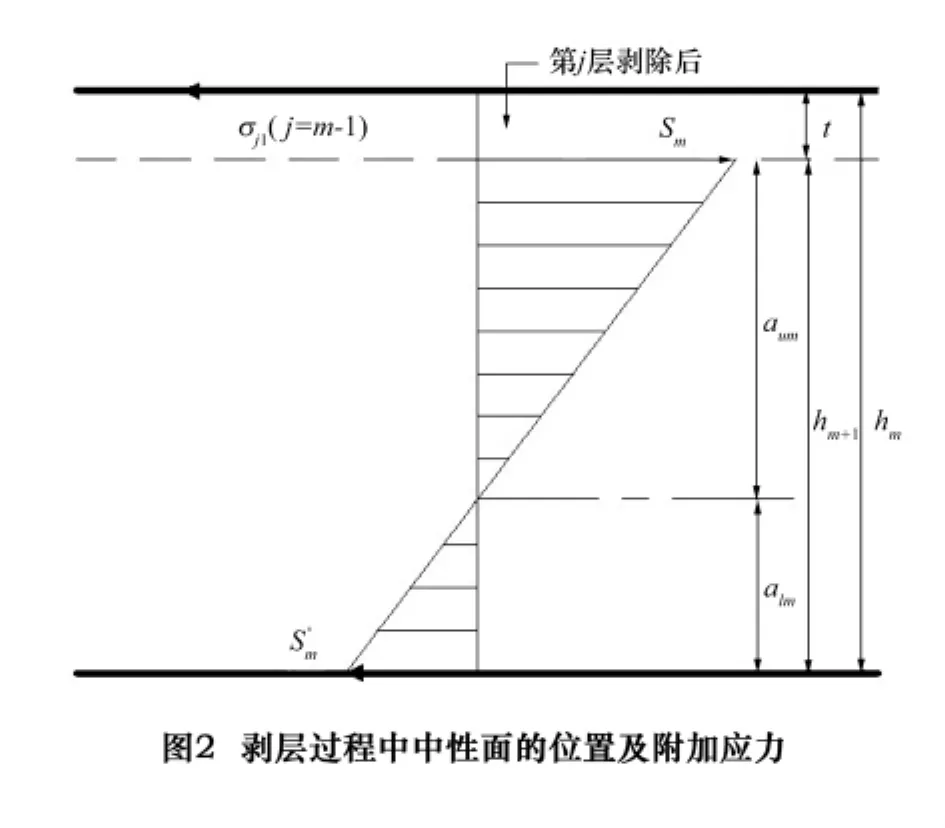
如果材料从上往下依次去除，如图2所示，当去除m层时，则第m层材料剥除前后的曲率变化为［7］

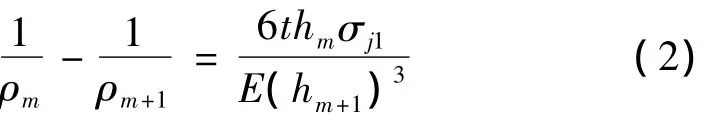
式中:ρm、ρm+1分别表示去除第m层材料前后工件的曲率半径;hm、hm+1分别为去除第m层材料前后的工件厚度;σj1为去除第m层前存在于该层的应力，j=m－1;t为剥层厚度;E为材料弹性模量。

当去除第m层材料后，剩余部分的变形挠度值为

式中:l为板的长度，曲率k=1/ρm+1。

根据力的平衡关系有:

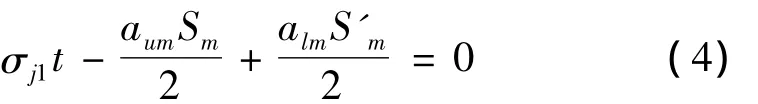
式中:Sm、S'm分别表示去除第m层引起工件材料剩余部分上、下表面的附加应力;aum为中性面至剩余部分上表面高度;alm为中性面至剩余部分下表面高度。

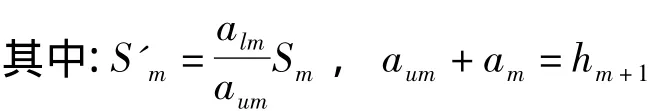
即得:

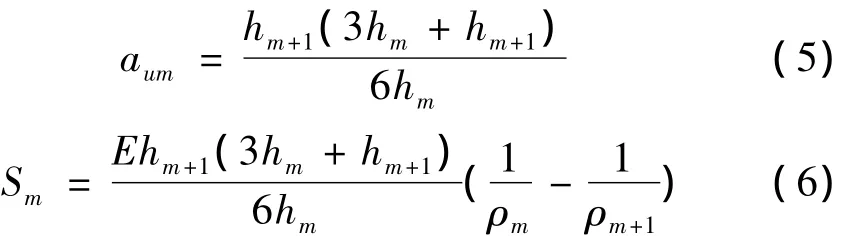
因去除m层后引起剩余各层内的附加应力Smi为

去除某一层后最上层的残余应力重新分布为

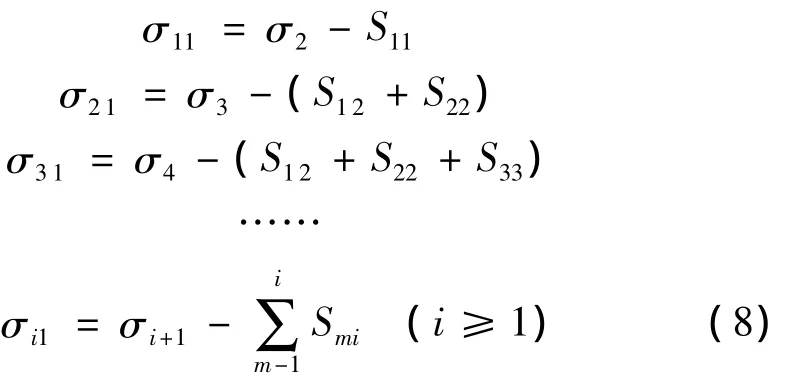
式中:σi1代表去除了i层材料后剩余材料最上层的残余应力值;σi+1表示工件原始第i+1层的初始残余应力值。

将式（8）代入式（2）得出:

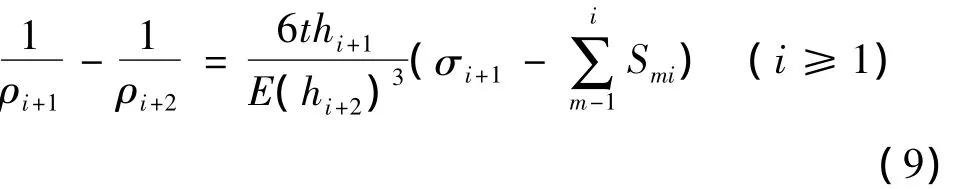
通过式（9）和式（3）可以计算出对应去除i层后工件的弯曲变形值。

2 正反面剥层初始残余应力对工件变形影响

设工件从上往下共分n层，从工件上表面开始进行加工，第1层材料去除后残余应力重新分布情况同上。当第2次加工材料（工件第n层）时，工件曲率变化与此层的应力关系式为

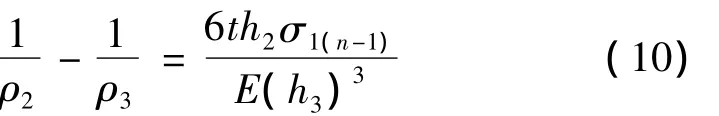
根据力的平衡关系有:

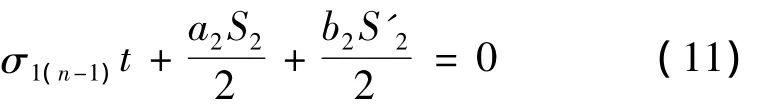
由胡克定律知:

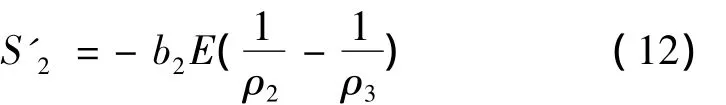
将式（10）～（12）联合求解得出:

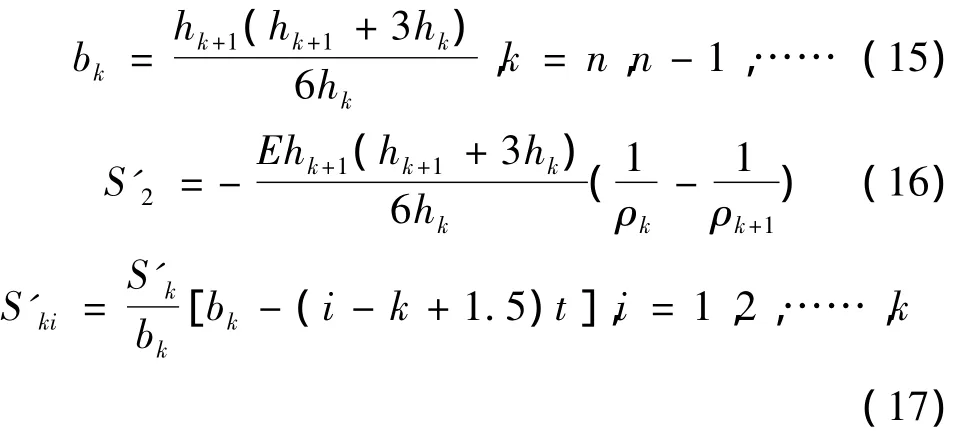
当剥除第k层时，可得出:其中:bk、ak分别为剥除第k层后，工件上、下表面到中性面距离，hk、hk+1为剥除第k层前后工件的厚度，S'k为剥除k层后材料下表面的残余应力;Ski为去除第k层后，引入剩余各层的附加残余应力。当剥除第n层后剩余各层的残余应力为:

第3次加工是工件的上表面第2层，当剥除上表面第2层时，施加的残余应力分布按照单面剥层情况的推导公式求解。综上，可得工件上下表面对称加工时，去除工件第i层前此层的残余应力为

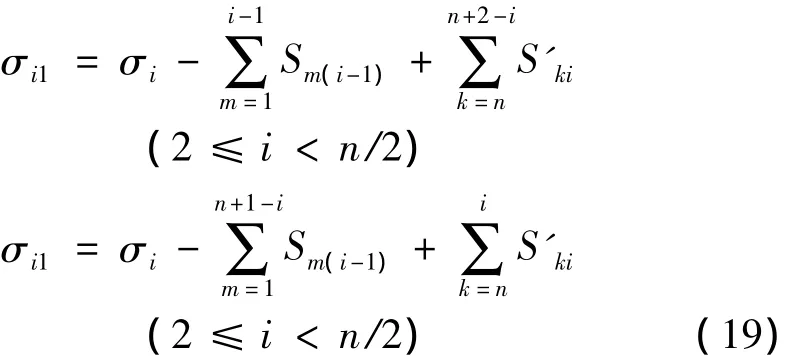
式中:i表示剥除工件总层数的任意一层。

将式（2）、（3）、（19）联立，可求出对应此层的工件弯曲挠度值。

3 铝合金7475初始残余应力引起的工件变形结果分析

毛坯材料为铝合金板件7475，弹性模量和泊松比分别为71 GPa和0.32，工件尺寸为500 mm×300 mm×20 mm。利用剥层法得到的毛坯初始残余应力进行离散化，按照“力平衡，力矩平衡”原则，得到各层的平均应力，如图3所示。

将图3中每层的初始应力值代入式（2）中，然后通过式（3）～（9）进行计算，得出对应单面剥层情况从上之下依次剥除对应各层的残余应力分布和工件变形值。

选用尺寸相同的铝合金7475矩形板进行高速铣削实验，机床为多棱三轴加工中心，刀具为直径100 mm的硬质合金面铣刀，前角 10°，后角7°，主偏角45°，刀尖圆弧半径0.8 mm。测量仪器:三坐标测量机。

切削参数:切削速度v=1 800 m/min，每齿进给量f齿=0.1 mm/齿，铣削深度ap=1 mm，进行分层切削。

每次铣削完一层后，进行时效处理，使得工件残余应力充分释放后，测量工件的变形挠度值与解析法求得的变形值进行对比，如图5所示。

通过图5可知，解析值和实验值是有一定误差的，主要是因为解析法假设残余应力是单向的，残余应力迭代时的附加应力也简化了，而且在实际加工中装夹力和切削力对工件变形也有一定的影响，使得实验值大于解析值，但变化趋势是一致的，验证了解析法的正确性。

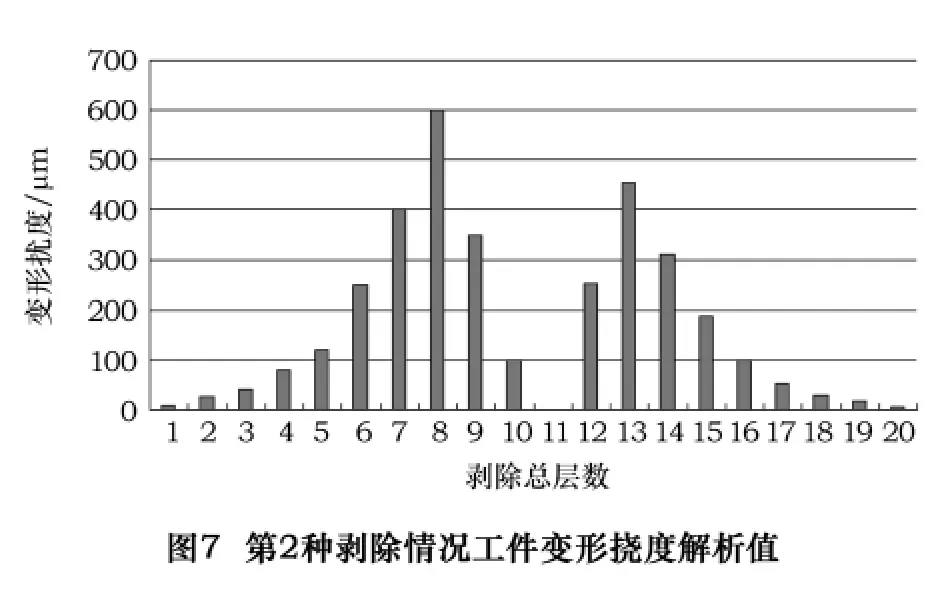
通过双面交替剥层情况，计算剥除某层后对应剩余层的残余应力重新分布和对应工件弯曲变形值分别如图6和图7。

4 结语

通过对上述两种剥层方法引起的工件变形和残余应力分布进行了解析法计算和实验验证，得出以下结论:

（1）在单面剥层情况下剥除材料时，在材料去除的初始阶段，工件的变形值随着剥层深度的增加而增加。当剥层深度达到13 mm时，变形程度最大，而后变形呈减小趋势，当剥层深度达到15 mm，工件两端的向上翘曲变形最小，继续剥层时工件开始向相反方向翘曲。

（2）当采用对称剥除材料方法得到的工件翘曲方向一直是一个方向，在初始阶段变形值有增大趋势，剥除总第8层后开始逐渐减小，最后剥除总第10层后变形值比第一种情况变形值小很多。说明采用对称去除材料方式能够驱使初始残余应力充分均匀的释放，有效地控制了工件变形。

（3）通过上述的解析方法可以分析残余应力引起的加工变形规律，获得最小变形时的最佳加工方法，对控制工件的变形有指导意义。

［1］Nervi Sebastian.A mathematical model for the estimation of effects of residual stresses in aluminum parts［D］.Washington University，USA，2005.

［2］Young Keith A.Machining－induced residual stress and distortion of thin parts［D］.Washington University ，USA，2005.

［3］黄志刚，柯映林，董辉跃.框类整体结构件铣削加工顺序的有限元模型［J］.浙江大学学报，2005，39（3）:368 －372.

［4］Guo H，Zuo D W，Wang S H，et al.The application of FEM technology on the deformation analysis of the aero thin一walled frame shape workpiece［J］.Key Engineering Materials，2006，315/316:174 －179.

［5］Guo H，Zuo D W，Yu Wei，et al.Simulation of effect of clamping on residual stress of aero components by measns of FEM［J］.7thICPMT，2004:730－734.

［6］王秋成.航空铝合金残余应力消除及评估技术研究［D］.杭州:浙江大学，2003.

［7］唐志涛.航空铝合金残余应力及切削加工变形研究［D］.济南:山东大学，2008.