滚珠丝杠磨削再生颤振稳定性极限预测*
迟玉伦 李郝林
(上海理工大学机械工程学院,上海 200093)
磨削是加工滚珠丝杠中的最后一道工序,磨削加工过程中发生的再生颤振是影响磨削工件质量的主要因素之一。再生颤振是一种典型的因振动位移延时反馈所导致的失稳现象,属于非线性振动,产生机理复杂,消振和减振十分困难[1]。在滚珠丝杠加工中,机床的振动不可避免,特别是砂轮与滚珠丝杠之间产生的再生颤振不仅影响滚珠丝杆的表面粗糙度和加工精度,还直接影响生产效率的提高。所以,如何有效分析和预测滚珠丝杠加工时的颤振稳定域成为一个关键技术[2-6]。
本文根据控制论中稳定性判据理论分析预测磨削系统的再生颤振稳定域,建立了滚珠丝杠磨削振动系统的动力学模型。通过大量磨削实验分析,实验验证了磨削颤振稳定性极限图预测的实用性。该颤振稳定性极限预测对优化磨削工艺参数提高加工质量和加工效率有重要意义。
1 滚珠丝杆磨削再生颤振模型
如图1所示,滚珠丝杠的两端分别被机床尾架顶尖和工件头架顶尖支撑顶紧;在滚珠丝杠磨削加工过程中,工件头架主轴带动滚珠丝杠转动,通过调整机床磨削砂轮与滚珠丝杠滚道的磨削角度进行磨削。

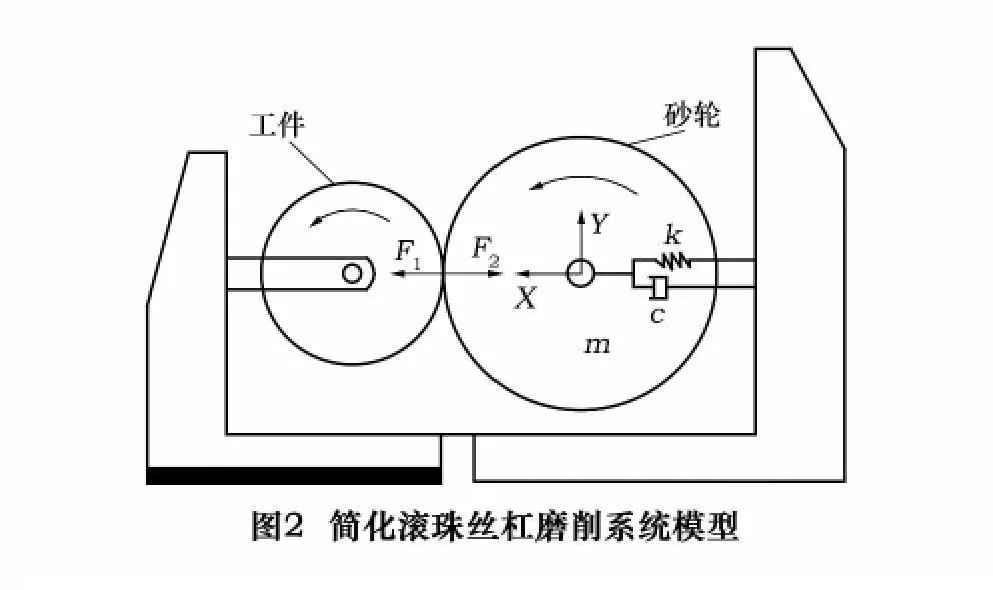
如图2所示,砂轮-滚珠丝杆磨削系统模型的示意图,该磨削动力学模型的运动微分方程可表示为

式中:m为机床振动系统等效质量,kg;c为机床振动系统等效阻尼,N·s/mm;k为机床振动系统等效刚度,N/mm;X(t)为t时刻砂轮振幅,mm;F(t)为动态磨削力,N。
以工件磨削深度方向为正方向,由材料去除率表示的动态磨削力F(t),可表示为
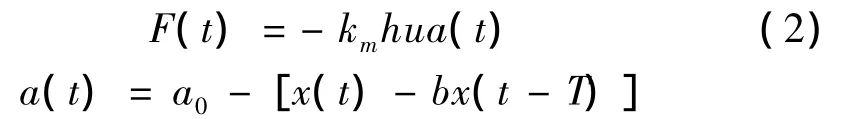
式中:km为砂轮磨削力系数,N/mm3;h为砂轮磨削深度,mm;u为磨削接触宽度,mm;a(t)为工件表面振纹,mm;b为砂轮前后两转的重叠系数;T为砂轮旋转周期,s;a0为初始表振纹。
通过拉氏变换,式(1)在频域中表示为

式中:s为拉氏算子,无量纲。
将磨削力F(t)的表达式式(2)经过拉氏变换后代入式(3),以X(s)作为颤振系统的输出,a0(s)作为输入,得到磨削系统的传递函数为

式中:W(s)为砂轮系统动柔度,m/N;ωn为砂轮系统固定角频率,rad/s;ζ为砂轮系统阻尼比,无量纲。
由控制原理可知,振动系统输出的时域特性取决于系统传递函数G(s)特征方程根s的性质。s可写成s=δ+jω的形式,当δ=0时,系统处于稳定与不稳定的临界状态。令δ=0,即可据此求得系统稳定性极限磨削深度hlim,将s=jω代入式(4)得

式中:ω为磨削砂轮颤振角频率,rad/s。
根据磨削砂轮颤振系统的传递函数式(6)及控制论中的稳定性判据,令式(6)传递函数的分母为零,可得到砂轮系统发生颤振条件,即
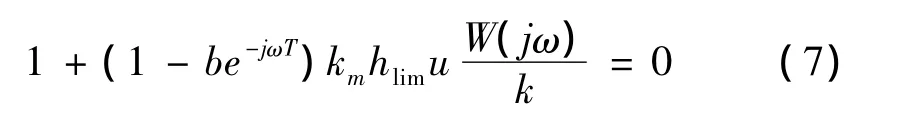
2 滚珠丝杠磨削再生颤振模型求解
令 λ = ω/ωn及e-jωT=cosωT-jsinωT,将式(5)代入式(7)后,经整理得
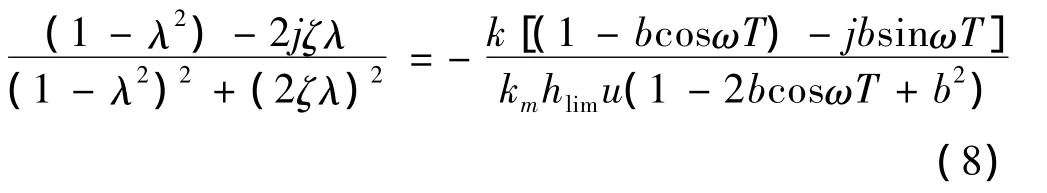
式中:ζ为振动系统阻尼比;ωn为振动系统固定角频率,rad/s。
根据复数相等的性质可知,等式左右两边实部与幅角分别相等,如式(9)和式(10)所示
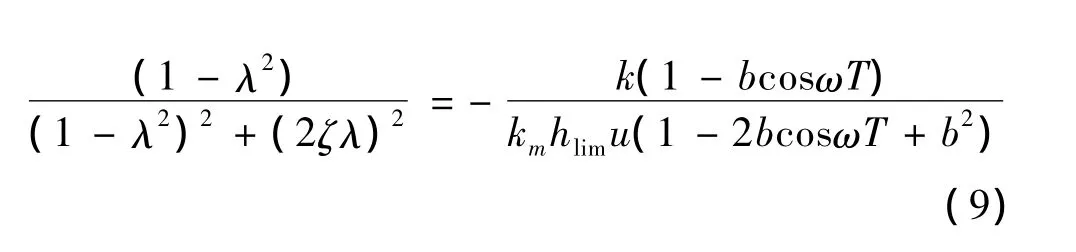

由式(6)、(9)和(10)可推得保证磨削过程稳定性的磨削深度h和砂轮主轴转速n分别为

由上述式(11)和式(12),可确定磨削中磨削深度hlim和砂轮主轴转速n颤振稳定性极限图。
3 实验研究
3.1 实验
本实验机床为SK7432万能外圆数控磨床,测量仪器为KISTLER振动分析仪。通过模态试验,对力激励下测得的机床振动加速度信号进行时域和频域分析,识别磨床砂轮结构的各阶固有频率及相关的模态参数。

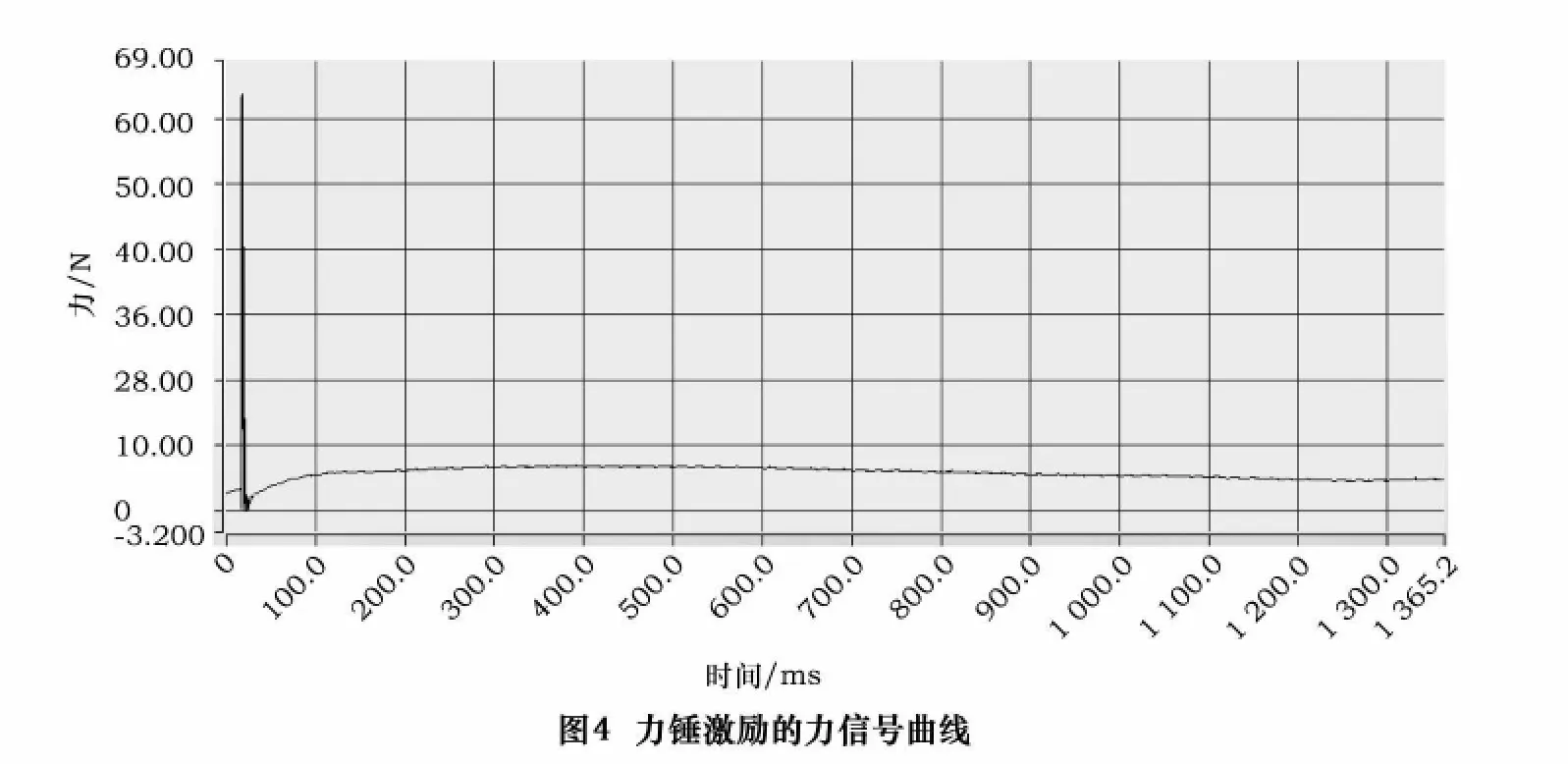
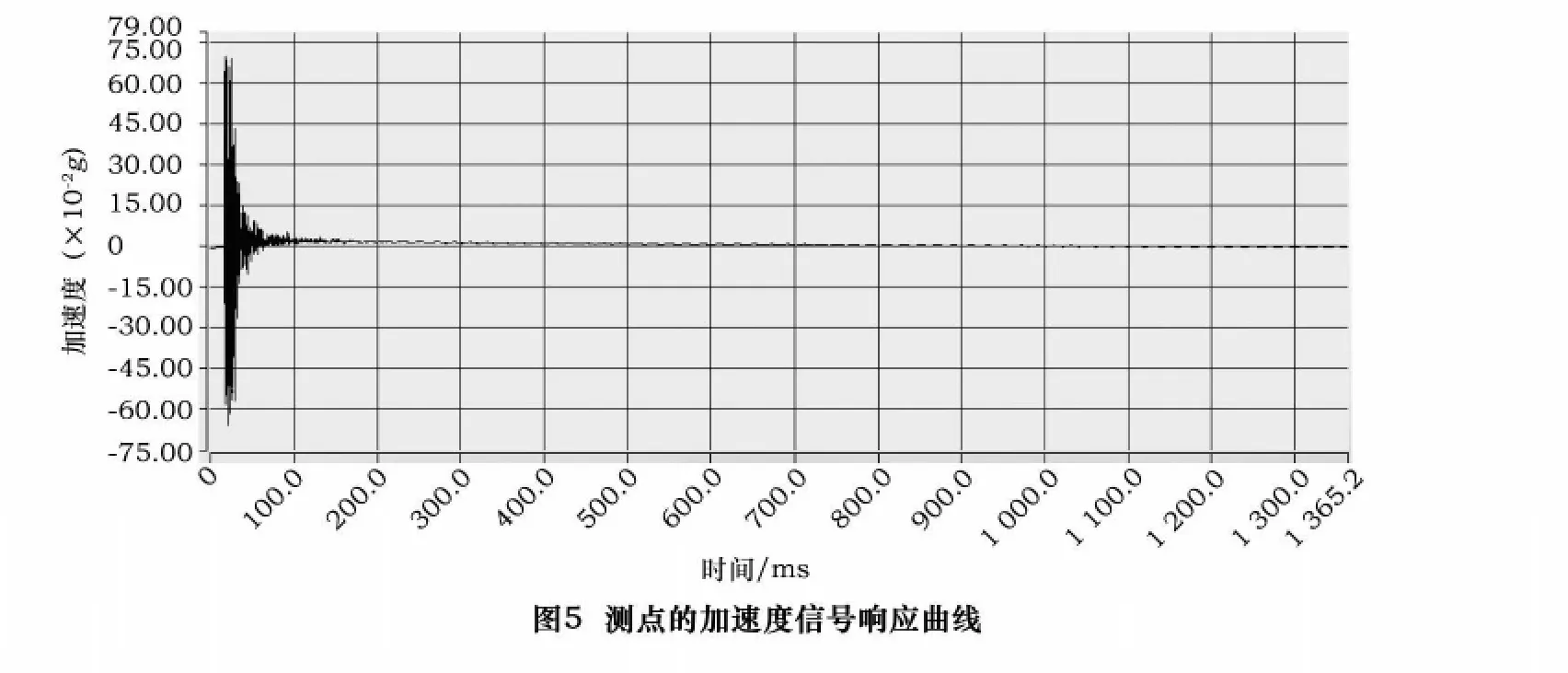
在磨床的砂轮架结构上设置振动传感器的响应测点,如图3所示。激励点设置在各响应测点附件,使用钢头力锤进行锤击。在模态试验过程中,应尽可能地减少随机误差和噪声对测量结果的影响。图4、图5分别为力锤激励的力信号和加速度响应信号随时间变化曲线。
通过模态实验分析及磨削工艺参数计算,可确定出式(11)和(12)的各机床动态特性参数如表1所示。
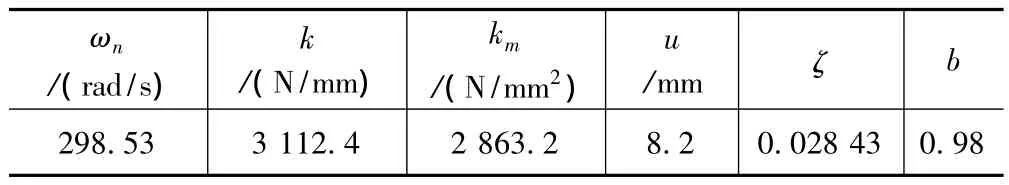
表1 机床动态特性各参数
3.2 磨削颤振稳定性极限图确定
稳定性极限图是用磨削深度与砂轮转速之间的关系来确定磨削过程中稳定磨削和不稳定磨削区域的临界条件。将表1中各机床动态特性参数值代入式(11)和(12)可确定磨削中磨削深度hlim和砂轮主轴转速n颤振稳定性极限图,如图6所示。图中耳垂线之上为不稳定区,耳垂线之下为稳定区。
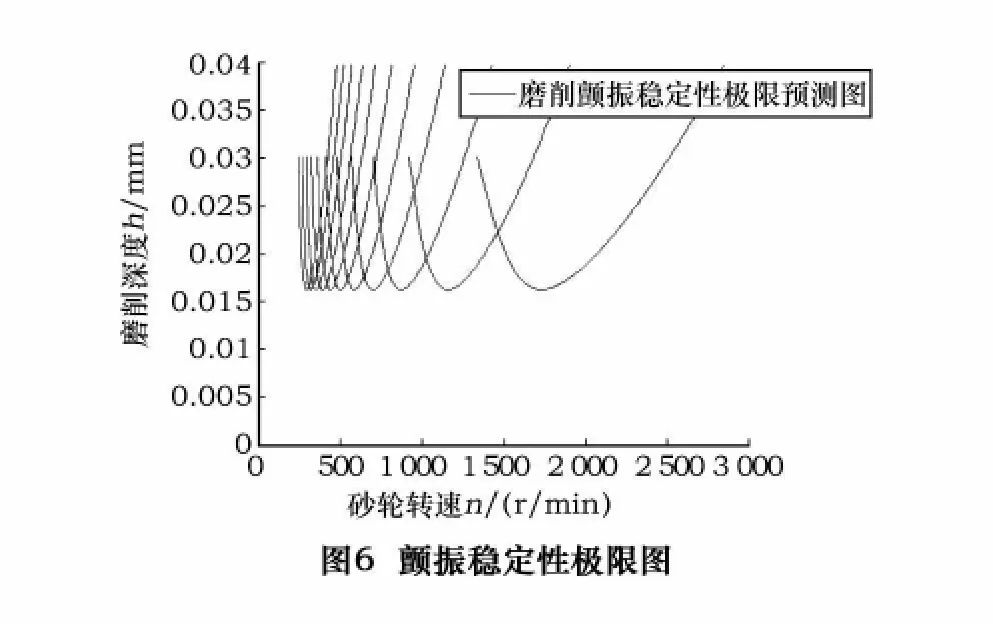
为验证上述颤振稳定性极限预测图的准确性,分别选取砂轮转速800 r/min、1 000 r/min、1 200 r/min和1 400 r/min进行磨削颤振实验。通过多次改变切削深度确定出各砂轮转速下发生颤振与未发生颤振的临界磨削深度h'lim。实验测量各砂轮转速与临界磨削深度的坐标为:(800 r/min,18 μm)、(1 000 r/min,17 μm)、(1 200 r/min,16 μm)和(1 400 r/min,20 μm)。
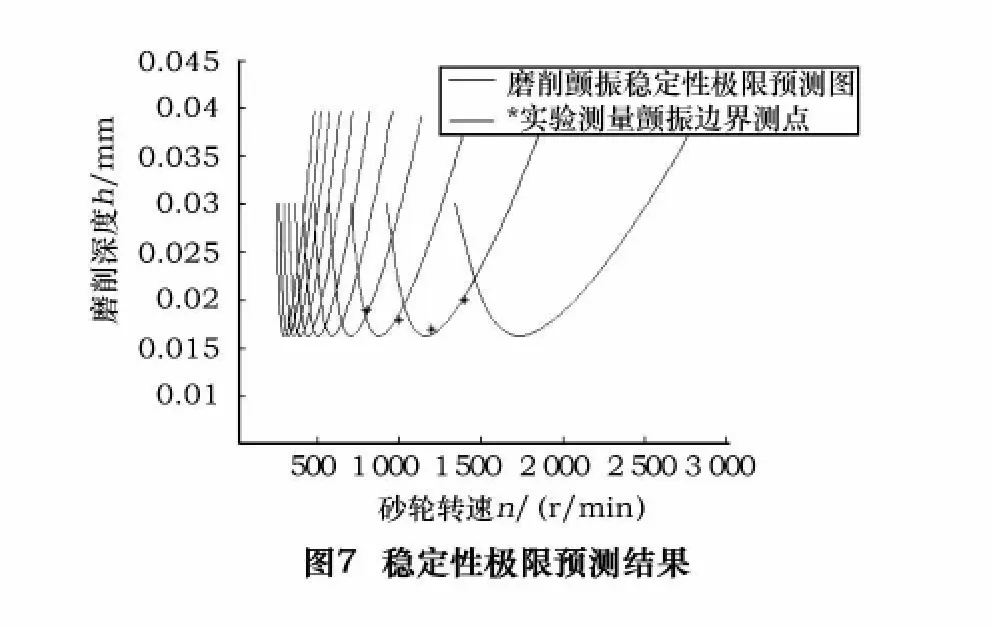
如图7所示,利用实验临界坐标测点验证上述图6中颤振稳定性极限预测图(图中星号点表示实验临界坐标测点)。如表2所示,列出在不同转速下稳定性图的预测磨削深度hlim、实验测量临界磨削深度h'lim和两个绝对值之差Δ=|h'lim-hlim|。计算结果Δ≤0.25,说明实验测量结果与理论预测曲线结果一致,验证了文中再生颤振稳定性极限预测方法的有效性。
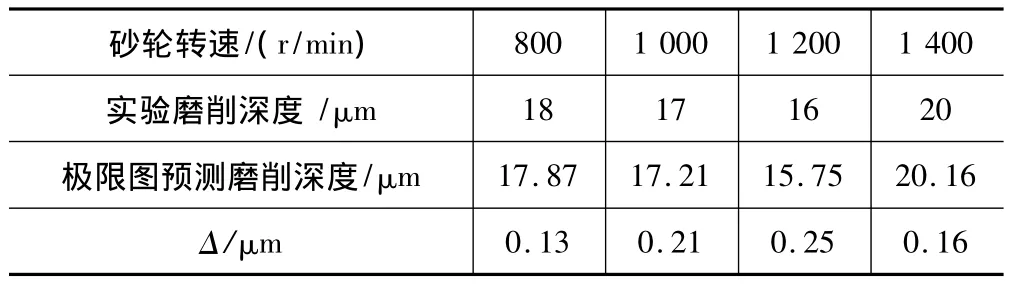
表2 各砂轮转速下临界磨削深度
4 结语
(1)基于再生颤振机理,对磨削滚珠丝杠振动系统进行动力学建模。
(2)根据动力学模型绘制出再生颤振稳定性极限预测图,并对该再生颤振模型进行磨削实验,实验验证了该理论预测与实验结果的一致性。
(3)该磨削颤振稳定性极限预测方法为机床加工人员选择正确切削参数提供理论依据,对提高磨削工件的表面质量和加工效率有重要意义。
[1]Gagnol V,Bouzgarrou B C,Ray P.Model- based chatter stability prediction for high-speed spindles[J].International Journal of Machine Tools and Manufacture,2007,47(7):1176 -1186.
[2]LI H,SHIN Y C.A study on chatter boundaries of cylindrical plunge grinding with process condition - dependent dynamics[J].International Journal of Machine Tools and Manufacture,2007,47(10):1563 -1572.
[3]马海龙,陈清奎,段辉.再生颤振的稳定性模型的研究[J].工具技术,2009,2:43 -45.
[4]汤爱君,马海龙.机床再生颤振系统研究现状的综述[J].机床与液压,2007,8(35):223 -225.
[5]INASAKI I,TONOU K,YONESTU S.Regenerative chatter in cylindrical plunge grinding[J].Bulletin of the JSME,1977,20(1):1648 -1654.
[6]WECK M,HENNES N,SCHULZ A.Dynamic behavior of cylindrical traverse grinding processes[J].CIRP Annals- Manufacturing Technology,2001,50(1):213 -216.
[7]蒋永翔,王太勇,黄国龙,等.外圆纵磨再生颤振稳定性理论及评价方法的研究[J].振动与冲击,2008,27(12):61 -63.

