Meta分析系列之一:Meta分析的类型

曾宪涛，冷卫东，郭毅，刘菊英

证据是循证医学(Evidence-based Medcine，EBM)的核心，基于随机对照试验(RCT)的系统评价/Meta分析是当前公认的最高级别证据。近些年来，随着Meta分析的不断推广，国内Meta分析大量涌现，这为临床实践提供了很好的支持。但因制作者的水平各异，使得Meta分析的质量良莠不齐，也给临床实践中使用者的选择带来了疑惑;再者，Meta分析只有真正走向临床并正确的使用，才能体现其价值，而当前Meta分析的应用较少。鉴于此，我们拟从Meta分析的类型、相关软件、原始研究质量评价、报告规范、Meta分析的质量评价等方面进行一个系列的讲解，以期为使用者提供参考。

本文作为第一篇，我们将对Meta分的起源和发展进行简要回顾后，对当前存在的Meta分析类型进行一个简介。希望通过本系列，使相关的读者能够撰写出较高质量的Meta分析并能将其在临床工作中进行运用。

1 起源及发展

Meta分析的起源最早可以追溯到著名统计学家Pearson，他于1904年在研究“血清接种预防肠热病的疗效”研究中用这一方法将接种肠热病疫苗与生存率之间的相关系数进行了合并［1］;1907年，Goldberger制作了特定的标准对所发表的有关伤寒杆菌尿毒症的文献进行选择及资料的提取分析，然后进行统计学分析，被认为达到了当今Meta分析的基本要求［2］;1920年，著名统计、遗传学家Fisher提出了“合并P值”的思想［3］，被认为是Meta分析的前身;1930年开始，Meta分析开始广泛应用了社会科学领域［2］。

直到1955年，Beecher［4］发表了医学领域第一篇真正意义上的Meta分析，用以评价安慰剂的疗效，并给予了Meta分析初步的定义;之后Meta分析在社会学领域再次得到发展，这一术语由英国教育心理学家Glass［5］于1976年命名并将其定义为:“The statistical analysis of large collection of analysis results from individual studies for the purpose of integrating the findings”。此后，关于Meta分析的定义一直存在争议，不少方法学家亦都对其下过定义，但都倾向于“Meta分析是对以往的研究结果进行系统定量综合的统计学方法”这一含义［3］。

如今，Meta分析在医学领域应用最为广泛，应用最多的是对干预性的随机对照试验的评价，在观察性研究和交叉对照研究中也得到推荐［6］。自Archie Cochrane奠定“循证医学”思想以来，Meta分析已成为临床证据的重要来源之一［7］。

2 单组率的Meta分析

单组率的Meta分析，是一种只提供了一组人群的总人数和事件发生人数，不像其它类的Meta分析有两组人群，多为患病率、检出率、知晓率、病死率、感染率等的调查，基于的原始研究为横断面研究(cross-sectional study)。

目前，对各独立样本中效应量为率的同类研究资料进行Meta分析并没有比较成熟的方法，较常用的有以下几种:①加权计算［8］:即根据每个独立研究的样本量大小，给予不同的权重，对各独立样本的效应量率进行合并;②直接等权相加［9］:即把各独立的结果事件直接等权相加，然后直接计算合并率，再用近似正态法计算其可信区间(95%可信区间=p±1.96 Sp);③调整后再等权相加［10］:即对各个独立研究资料的率进行调整后再行等权相加，计算出合并率的大小。

对单组率的Meta分析而言，最难的就是控制异质性，进行亚组分析和Meta回归分析是其重要的处理方法［8-9］。

3 单纯P值的Meta分析

1932年，著名统计学家Fisher提出了“合并P值”的思想，被认为是Meta分析的前身［3］。但在后期的应用中许多学者发现单纯合并P值存在以下不足［11-12］:不同研究未能根据研究特点进行加权;无法获知事件的发生信息，故无法得出有任何临床意义的信息;③无法分析两个结论相反的研究;④无法进一步评价研究之间的差异。

因此，单纯行P值的Meta分析是不推荐的。但当纳入研究仅给出了P值，且按照Cochrane系统评价员手册［13］给出计算方法也不能计算出需要的数据，且临床实践需要合并，那么，在这种情况下可以考虑单纯对P值进行合并。

4 Meta回归分析

在Meta分析时，需分析各研究间的异质性，并对异质性的来源进行探讨，Meta回归(meta-regression)分析可评价研究间异质性的大小及来源。一般认为，Meta回归分析是亚组分析的一种扩大，主要通过对多因素的效应量进行联合分析实现，仅当Meta分析纳入的研究数量在10个以上时才行此分析［13-15，28］。

在Meta回归里，将效应估计量(如RR、OR、MD或logRR等)作为结果变量，将可影响效应量大小的研究特征因素(“协变量”或“潜在效应量改变因子”)作为解释变量，则回归系数描述了结果变量怎样随着解释变量的单位增加而改变;其统计学差异性通过对结果变量和解释变量之间有无线性关系来确定，通过回归系数的P值来判断这种差异有无统计学意义［13-15，28］。

5 累积Meta分析

累积Meta分析(cumulative meta-analysis)最早应用于1981年，是指将研究资料作为一个连续的统一体，按研究开展的时间顺序及时将新出现的研究纳入原有Meta分析的一种方法［16-19，28］。因此，Meta分析每次研究加入后均重复一次Meta分析，可以反映研究结果的动态变化趋势及各研究对结果的影响，也有助于尽早发现有统计学意义的干预措施。

6 间接比较的Meta分析

在临床实践中，经常会碰到没有直接比较的证据或者需要从众多干预措施中选择对患者最佳的措施，此时，研究者往往会从RCT中寻找间接证据，这就形成了间接比较的Meta分析或多种干预措施比较的 Meta分析(网状 Meta分析)［20-21］。

6.1两因素间接比较若想比较两种干预措施A与B的效果，但当前没有两者的直接比较的RCT，却有两者同干预措施C的比较，此时，可以将C作为公共比较组，借助间接比较的方法得出A与B的效果。

间接比较包括未调整间接比较和调整后间接比较［20，22-23］。未调整间接比较是直接从RCT中提取A与B的数据，此方法虽然简单但对随机性的破坏很大，故可能产生较大偏倚从而高估疗效，现已不推荐使用。调整后间接比较以C作为公共比较组(C可以是安慰剂或阳性对照组)，与未调整间接比较相比其最大的的优势是能够在一定程度上保留随机特性，且经过了同质性和相似相检验，因而偏倚较小，为当前推荐的方法(图 1)［23］。

图1 调整后间接比较示意图

6.2网状Meta分析在临床实践中，若有一系列的药物可以治疗某种疾病，但RCT均是药物与安慰剂的对照，而药物互相之间的RCT都没有进行或很少，那么在这种情况下，就需要将间接比较和直接比较的证据进行合并，即行网状Meta分析(network meta-analysis)(图 2)［21］。

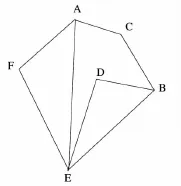
图2 网状Meta分析示意图

行网状Meta分析首要的是构造一个等级模型，以处理抽样变异、治疗异质性及研究治疗比较间的不一致性，并提供模型的最大似然比。目前，主要的方法有经典的频率学法和贝叶斯法。频率学法目前主要应用的有倒方差法和广义线性(混合)模型。倒方差法即将各研究的方差倒数作为权重，对各研究效应进行加权平均，总体效应的方差为权重之和的倒数，操作相对简单;广义线性模型则考虑了随机效应，但应用的前提是需要获得受试者个体数据。贝叶斯法是基于贝叶斯定理而发展而来的，与频率学方法相比，其优势在于可以利用后验概率对所有分析的干预措施进行排序，且克服了频率学法在参数估计时通过不断的迭代去估计最大似然函数、易出现不稳定而得到有偏倚的结果的缺陷，故估计值更为准确，且建模更灵活，为当前所推荐的方法［24-25］。

7 诊断性Meta分析

因地区、个体、诊断方法及条件的差异，使得发表的关于同一诊断方法的研究结果存在着不同甚至是矛盾的;且随着新技术的不断走向临床，选择也愈来愈多。诊断性Meta分析是近年来出现的，并为“诊断试验准确性研究的报告规范(STARD)”指导小组［26］和“Cochrane协作网”［13］所推荐。

诊断性Meta分析主要是为评价某种诊断措施对目标疾病的准确率，多为对目标疾病的敏感性、特异性进行评价，报道似然比、诊断比值比等。若是为了评价某种诊断措施对目标疾病的诊断价值，则一般纳入的应为病例对照研究，对照组多为健康人群;此外，若是为评价运用诊断措施后对患者的治疗效果或预后效果的改善作用，则纳入的原始研究应为RCT，这两种情况下行Meta分析的方法亦与防治性研究的Meta分析相同［26-27］。

8 个体数据Meta分析

个体数据(individual patient data，IPD)Meta分析是近年来发展起来的一种特殊类型，其不是直接利用已经发表的研究结果总结数据进行Meta分析，而是通过从原始研究作者那里获取每个参与者的原始数据，并对这些数据进行Meta分析［13］。

与常规Meta分析相比，个体数据Meta分析具有以下优点:能够最大限度的纳入未发表的试验或灰色数据，能够进行时间-事件分析，能够更新长期随访的数据，能够进行更复杂的多变量统计分析;但耗费大量时间、资源等是其最大的缺陷。目前，建立在IPD基础上的Meta分析被称为系统评价的金标准［13］。

9 前瞻性Meta分析

前瞻性Meta分析(prospective meta-analysis，PMA)是指在RCT的结果尚未出来之前，先进行系统检索、评价和制定纳入及排除标准的一种Meta分析。因PMA是在研究开始之前或者进行中就制定好了计划，可以避免各研究间出现较大的差异，同时具有个体数据Meta分析的优点［13］。当前认为，PMA是针对需要行多中心、大样本研究但现实又不能实现的情况下的最有效方式，但成本非常高、操作困难且需要耗费大量的时间。

10 常规Meta分析

当前，常规Meta分析主要基于有对照组的直接比较的研究，最常见的是基于RCT的干预性Meta分析，此外，还有预后研究、动物实验、病因研究、基因多态性等的Meta分析。基于的原始研究类型还有队列研究、病例对照研究、群随机对照试验、自身对照试验等［3，12-13，28］。

11 其他类型Meta分析

近年来，随着方法学的研究进展及循证实践的实际需求，出现了许多上述未涉及到的Meta分析，主要有:不良反应的Meta分析，成本-效果/效用/效益的Meta分析，患者报告结局的Meta分析，全基因组关联研究的Meta分析，Meta分析的汇总分析，等［13，29-30］。

结语:毫无疑问，高质量的证据是循证医学实践取得成功的重要支撑，高质量的Meta分析则是其重要的保障。随着Meta分析知识的普及及方法学的不断改进与广泛应用，其质量将进一步提高，从而真正为医疗卫生和预防实践提供更科学的证据。

［1］Pearson K.Report on Certain Enteric Fever Inoculation Statistics［J］.Br Med J，1904，2(2288):1243-1246.

［2］Winkelstein W Jr.The first use of meta-analysis［J］?Am J Epidemiol，1998，147(8):717.

［3］Egger M，Smith GD，Altman DG.Systematic reviews in health care.Meta-analysis in context［M］.2nd edition.London:BMJ Publishing Group，2001.

［4］Beecher HK.The powerful placebo［J］.JAMA，1955，159(17):1602-1606.

［5］Glass G.Primary，secondary and meta-analysis of research［J］.Educ Res，1976，5:3-8.

［6］Egger M，Smith GD.Meta-Analysis.Potentials and promise［J］.BMJ，1997，315(7119):1371-1374.

［7］Cochrane AL.Archie Cochrane in his own words.Selections arranged from his 1972 introduction to"Effectiveness and Efficiency:Random Reflections on the Health Services"1972［J］.Control Clin Trials，1989，10(4):428-433.

［8］Sutton AJ，Abrams KR，Jones DR，et al.Methods for Meta-Analysis in Medical Research［M］.Chichester:John Wiley ＆ SonsLtd，2000.

［9］Ali SA，Donahue RM，Qureshi H，et al.Hepatitis B and hepatitis C in Pakistan:prevalence and risk factors［J］.Int J Infect Dis，2009，13(1):9-19.

［10］Batham A，Narula D，Toteja T，et al.Sytematic review and meta-analysis of prevalence of hepatitis B in India［J］.Indian Pediatr，2007，44(9):663-674.

［11］Jones J，Hunter D.Consensus methods for medical and health services research［J］.BMJ，1995，311(7001):376-380.

［12］Sterne JA.Meta-Analysis in Stata:An Updated Collection from the Stata Journal［M］.Stata Press，2009.

［13］Higgins JPT，Green S.Cochrane Handbook for Systematic Reviews of Interventions Version 5.1.0［updated March 2011］.The Cochrane Collaboration，2011.Available from www.cochrane-handbook.org.

［14］Berkey CS，Hoaglin DC，Antczak-Bouckoms A，et al.Meta-analysis of multiple outcomes by regression with random effects［J］.Stat Med，1998，17(22):2537-2550.

［15］Thompson SG，Higgins JP.How should meta-regression analyses be undertaken and interpreted?［J］.Stat Med，2002，21(11):1559-1573.

［16］Berkey CS，Mosteller F，Lau J，et al.Uncertainty of the time of first significance in random effects cumulative meta-analysis［J］.Control Clin Trials，1996，17(5):357-371.

［17］Baum ML，Anish DS，Chalmers TC，et al.A survey of clinical trials of antibiotic prophylaxis in colon surgery:evidence against further use of no-treatment controls［J］.N Engl J Med，1981，305(14):795-799.

［18］Hu M，Cappelleri JC，Lan KK.Applying the law of iterated logarithm to control type I error in cumulative meta-analysis of binary outcomes［J］.Clin Trials，2007，4(4):329-340.

［19］Muellerleile P，Mullen B.Sufficiency and stability of evidence for public health interventions using cumulative meta-analysis［J］.Am J Public Health，2006，96(3):515-522.

［20］Song F，Altman DG，Glenny AM，et al.Validity of indirect comparison for estimating efficacy of competing interventions:empirical evidence from published meta-analyses［J］.BMJ，2003，326(7387):472.

［21］Lumley T.Network meta-analysis for indirect treatment comparisons［J］.Stat Med，2002，21(16):2313-2324.

［22］Glenny AM，Altman DG，Song F，et al.Indirect comparisons of competing interventions［J］.Health Technol Assess，2005，9(26):1-134，iii-iv.

［23］Song F，Loke YK，Walsh T，et al.Methodological problems in the use of indirect comparisons for evaluating healthcare interventions:survey of published systematic reviews［J］.BMJ，2009，338:b1147.

［24］Dias S，Welton NJ，Caldwell DM，et al.Checking consistency in mixed treatment comparison meta-analysis［J］.Stat Med，2010，29(7-8):932-944.

［25］Buti J，Glenny AM，Worthington HV，et al.Network meta-analysis of randomised controlled trials:direct and indirect treatment comparisons［J］.Eur J Oral Implantol，2011，4(1):55-62.

［26］Bossuyt PM，Reitsma JB，Bruns DE，et al.Towards complete and accurate reporting of studies of diagnostic accuracy:The STARD Initiative［J］.Radiology，2003，226(1):24-28.

［27］Battaglia M，Bucher H，Egger M，et al.The Bayes Library of Diagnostic Studies and Reviews［M］.2nd edition，2002.

［28］Borenstein M，Hedges LV，Higgins JPT，et al.Introduction to Meta-Analysis［M］.Chichester:John Wiley ＆ SonsLtd，2009.

［29］Ioannidis JP，Patsopoulos NA，Evangelou E.Heterogeneity in metaanalyses of genome-wide association investigations［J］.PLoS One，2007，2(9):e841.

［30］Lohmueller KE，Pearce CL，Pike M，et al.Meta-analysis of genetic association studies supports a contribution of common variants to susceptibility to common disease［J］.Nat Genet，2003，33(2):177-182.