锻锤的弹簧隔振技术
文/尹学军,王伟强,姜成,邱永钢·隔而固(青岛)振动控制有限公司
锻锤的弹簧隔振技术
文/尹学军,王伟强,姜成,邱永钢·隔而固(青岛)振动控制有限公司

锻锤设备工作时,会产生强烈的冲击振动和噪声。振动的传递会影响周围设备的正常工作,危害周围人员的健康,同时也会对设备本身造成影响,提升了设备故障率。因此,锻锤设备必须进行隔振。在诸多隔振措施中,橡胶、枕木、砂垫、防振沟等隔振材料和隔振方式,因为隔振效果不明显,现已不再采用。目前,企业主要采用由钢螺旋弹簧和粘滞阻尼器组成的弹簧阻尼隔振器。这种低调谐的隔振系统隔振效果最好,但如果设计不当,也达不到预期的效果。
弹簧隔振的原理
与回转机械产生的连续、稳定的正弦波形函数激振力不同,锻造设备产生的是断续、不稳定的冲击性脉冲载荷。脉冲载荷的波形有很多种,选取两种典型的波形进行研究,来探讨锻锤设备的弹簧隔振原理。这两种波形,一种是矩形脉冲,其特点是激振力在作用周期开始的瞬间就达到峰值;另一种是半正弦波形脉冲,激振力增加得比较慢,从零逐渐增加到峰值,如图1所示。
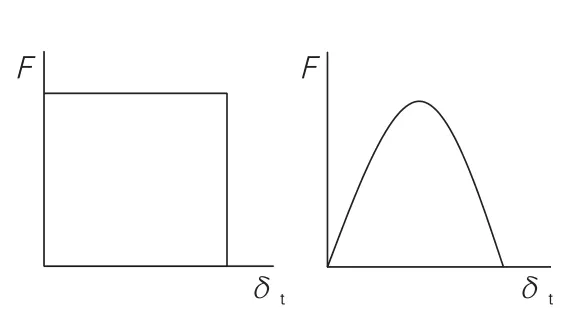
图1 矩形脉冲波(左图)与半正弦脉冲波(右图)
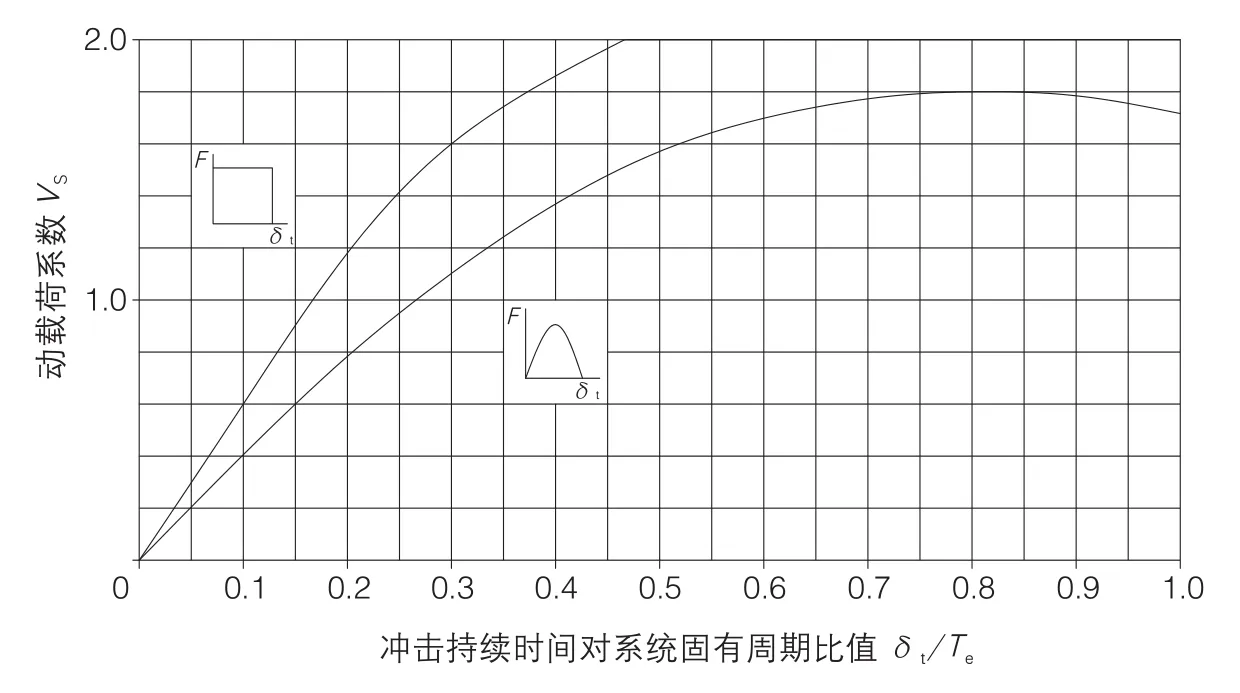
图2 冲击激振的动载荷传递系数
对于脉冲载荷,有两个主要性能参数,一个是脉冲载荷的持续作用时间δt,另一个是载荷峰值F。在一个无阻尼的弹簧隔振系统中,包括锻锤、基础块(如果需要)和弹簧隔振器,系统固有周期(固有频率的倒数)为Te。对于这个系统的传递力而言,最重要的参数为脉冲载荷作用时间与系统固有周期的比值δt/Te。研究揭示,对矩形脉冲而言,当冲击持续时间与系统固有周期的比值δt/Te>0.5时,动载荷系数(传递力与激振力的比值)等于常量2;对半正弦脉冲而言,当δt/Te=0.85时,动载荷系数的最大值为1.8,见图2。δt/Te>0.5时,多半为刚性基础,其传递到基础上的力总是大于输入的激振力,即动载荷系数大于1。
图2表明,只有当δt/Te<0.167(对矩形脉冲)或δt/Te<0.267(对半正弦脉冲)时,才能使动载荷系数Vs<1,即传递力小于输入力。这要求弹簧隔振系统的固有周期至少是矩形脉冲的6倍,或是半正弦脉冲持续时间的3.75倍才能实现。弹簧隔振系统由于系统频率低(系统周期大),可以满足这个要求。举例来说,锻锤设备弹簧隔振系统的固有频率为fe=6Hz,即Te=1/6=0.167s,矩形脉冲持续时间为δt=25ms,得比值δt/Te=0.025/0.167=0.15。由图2查得,动载荷系数约为0.9<1,可以实现传递力小于输入力。根据图2可知,只要系统固有频率小于6.7Hz,就能满足传递力小于输入力的要求。
阻尼比的大小会对隔振系统的效果产生重要的影响。对于回转机械的隔振系统,选取的系统阻尼比一般不超过0.15;对于锻锤设备的隔振系统,需要的阻尼比要更大一些,一般取到0.25左右。也许,会有人担心阻尼比过大会影响传递力,影响动载荷系数。其实不然,阻尼比适当加大可以有效地降低锻锤工作时的振幅,降低传递力,但并不是越大越好。
根据研究,锻锤的振幅大小和传递力大小与阻尼比具有以下关系:随着阻尼比的增加,锻锤振幅会不断减小,在阻尼比大约等于0.25时,得到最小值,但通过阻尼器传递的力会先减小后增加。与无阻尼弹簧系统比较,此时振幅约为无阻尼弹簧系统的70%,传递力约为无阻尼弹簧系统的80%,如图3所示。阻尼比为0.25之后,若阻尼比再增加,传递力不减反增,通过阻尼器传递的力将大幅度地增加。也就是说,如果在隔振时过分追求锻锤工作的小振幅,就必须依靠增加系统的阻尼比或者增加弹簧的刚度来实现,但无论怎么做,都会导致传递到基础上的力变大,使隔振效率降低。
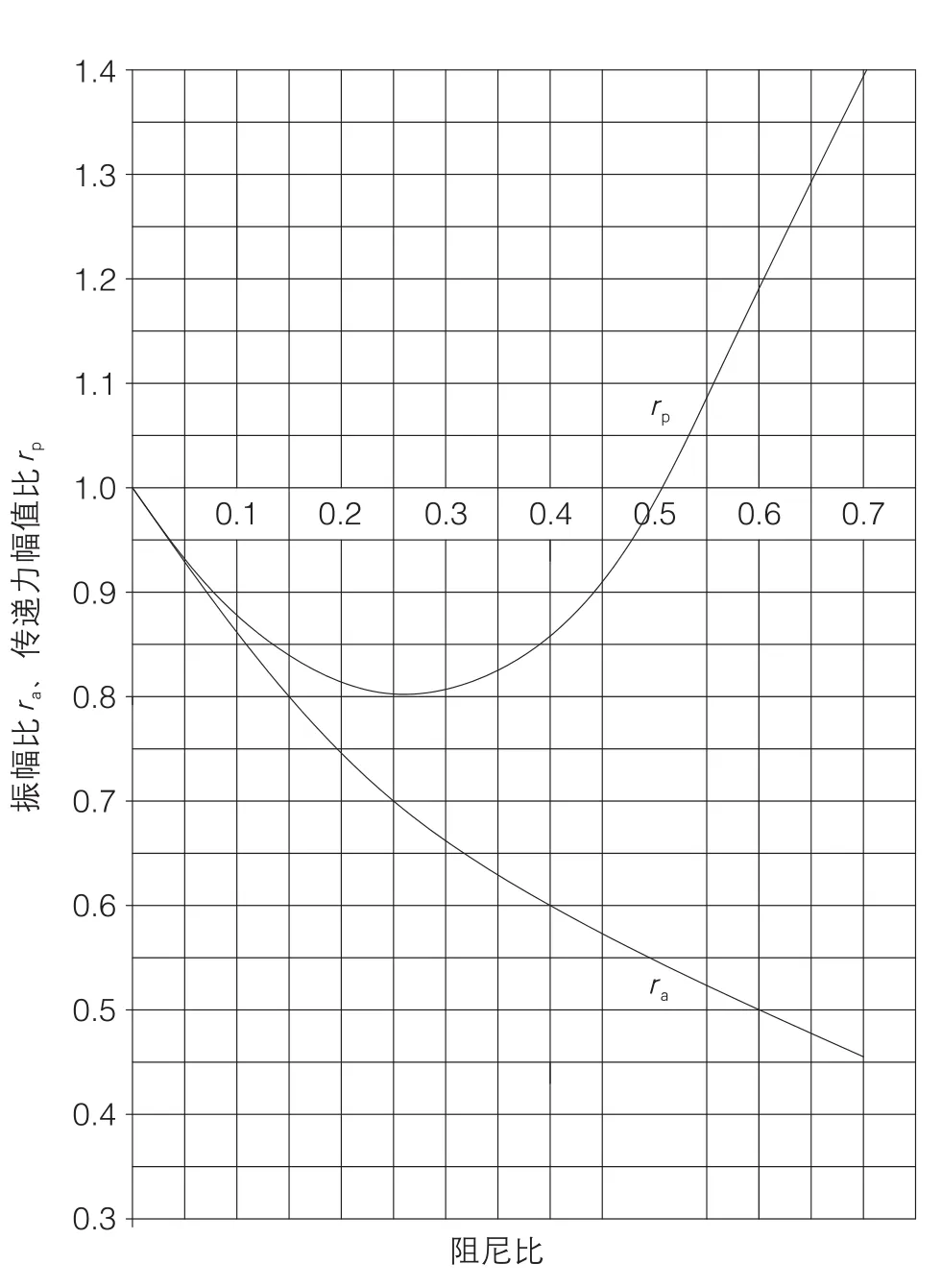
图3 振幅、传递力幅值与阻尼比的关系
研究揭示的规律可以概括为两点:
⑴要使传递力小于输入的激振力,必须使系统的频率尽可能小于6.7Hz,也即垂向压缩量必须大于5.6mm,这对于钢制螺旋弹簧很容易实现。但是橡胶、枕木、砂垫等都比较难于满足要求,防振沟对低频振动起不到任何隔振作用,除非挖15~20m深的防振沟,否则振动波可以绕过沟底传播。
⑵阻尼对降低振幅与传递力起很大作用,但又不是越大越好。实践证明,锻锤隔振系统的最佳阻尼比应为0.25。
锻锤隔振系统的隔振效率
对一个冲击脉冲,如果隔振系统输入脉冲力峰值为FC,传递脉冲力峰值为FA,则隔振效率用公式(1)表示:

对于脉冲载荷,输入脉冲的持续时间是可以测量的,但输入脉冲力峰值FC通常很难知道。无阻尼隔振系统,通过测量系统响应振幅乘以总弹簧刚度算得输出脉冲力峰值;有阻尼隔振系统,还要加上系统响应速度峰值与总阻尼系数的乘积。
用测量锻锤上加速度与紧挨隔振系统的地面加速度,来评估隔振系统的隔振效率不可取。因为在锻锤上测得的大加速度,通常来自锻锤本身高固有频率振动。这些高固有频率,即使不隔振也不会传递,而且在下层基础上也只传递很短距离就衰减了。所以机器周围测得的加速度很小,由此计算的隔振效率大大偏高,不反映真实值。
锻锤隔振系统隔振效率的评估标准,应该在靠近锻锤某个相同的地点,比较不隔振基础与隔振基础的振动水平。这个评估标准,必须使机器首先用不隔振基础,再用隔振基础测量两次才能实现。
当系统固有周期系统Te远大于脉冲载荷的作用持续时间δt,即δt远远小于Te时,假设不隔振基础传递力为FB,隔振基础传递力为FA,则隔振系统的隔振效率可以用公式(2)计算:
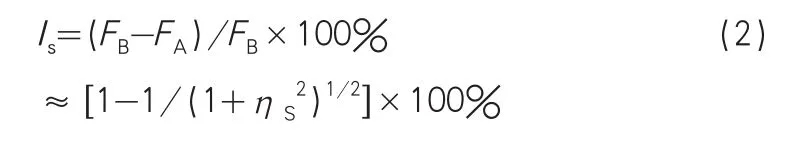
式中,ηS=fB/fe
fB──机器加基础支承在弹性下层基础(不隔振)上的固有频率,一般为10~20Hz以上;
fe──弹簧支承系统的固有频率,一般为3~5Hz。
假定,fe远远小于fB,则公式(2)可简化为公式(3):
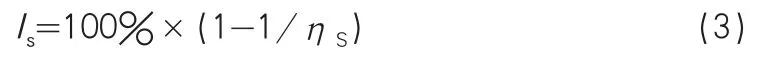
图4所示的隔振效率曲线,表示不同频率比ηS下隔振效率Is曲线。
图4 隔振效率曲线

图5 隔振示意图
锻锤隔振技术的发展历史
不隔振的锻锤固定基础如图5a所示,锻锤通常被安装在一个很大的固定基础上面,由这个固定基础来缓冲锻锤工作时的冲击载荷。在20世纪50年代,隔而固(青岛)振动控制有限公司开发出了由螺旋弹簧、粘滞阻尼器与基础块组成的锻锤隔振基础,见图5b,基础块尺寸比固定基础小很多。70年代,隔而固(青岛)振动控制有限公司针对自身质量相当大的锻锤,又开发出了没有基础块的直接支承式弹簧基础,见图5c;对自身质量小的锻锤,可以先增加一个附加质量,然后再支承在弹簧隔振器上,这样既能保证隔振效果,又简化了施工。根据地基基础动、静力学分析,地基底板厚度为0.50~1.0m。对于自由锻锤来说,由于锤身和砧座是分离的,通常需要增加一个基础块将其连接在一起,然后再进行隔振,图5d显示的为典型的自由锻锤的弹簧隔振基础。为了验证隔振效果,隔而固公司对一些搬迁改造的锻锤设备进行了振动测试,表1列举了这些锻锤固定基础与弹簧隔振基础的振动速度。测量点位于距锻锤中心10m处。
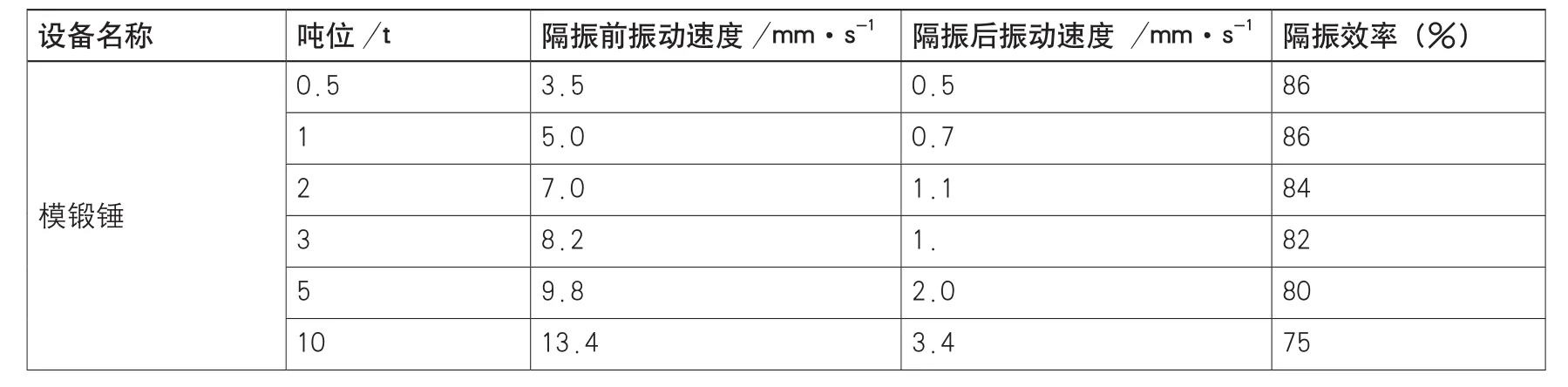
表1 各种吨位锻锤固定基础与弹簧隔振基础的振动速度实测值
锻锤隔振系统的构成
锻锤弹簧隔振系统由螺旋弹簧、基础块(如果需要)和粘滞阻尼器组成,如图6所示。弹簧隔振系统的核心元件是弹簧与阻尼器,组装在一起称之为弹簧阻尼隔振器,见图7。弹簧的主要作用是降低系统固有频率,使传递力降低到小于输入脉冲力;粘滞阻尼器的作用是让弹簧隔振系统的阻尼比达到D=0.25左右,从而达到最佳隔振效果。锻锤用弹簧要承受巨大的交变应力,因此必须采用材质优良、淬透性能好的合金钢材;粘滞阻尼器必须提供通过试验实测的、参数准确的阻尼系数和使用性能稳定并抗老化的阻尼介质。

图6 锻锤弹簧隔振系统结构

图7 弹簧与阻尼器组成整体结构的隔振器
设计一台锻锤的弹簧隔振系统需要用户提供以下主要技术参数:
⑴制造厂家和型号。
⑵锻锤质量。
⑶下落部分质量。
⑷最大打击能量。
⑸砧座底部尺寸。
⑹砧座在地面下的深度。
⑺地质资料。
结束语
为了使基础传递力小于输入的脉冲力,必须使系统的垂向固有频率尽可能低于6.7Hz;为了取得最佳隔振效果,系统阻尼比应尽可能接近0.25,隔而固(青岛)振动控制有限公司的弹簧隔振技术能保证这两大特性的实现。且经实测数据证明,其隔振效率通常可以达到80%以上。
尹学军,德国工学博士,隔而固(青岛)振动控制有限公司总经理,中国工程建设标准化协会建筑振动专业委员会副秘书长,中国环境保护产业协会噪声与振动控制委员会常务委员。

