基于分布式偏好理论的Luce-Suppes难题之消解

王志远

(广西民族师范学院政治与公共管理系，广西崇左532200)

选择理论一般假定选择依赖于偏好［1］，而实际的选择情景也表明，行动主体做出选择确实是建立在偏好基础上的，无论选择时所形成的偏好是理性的表达，还是非理性激发的结果。可见偏好在选择理论中的重要作用。此外，或重大，或微小，一个人一生会不断地处于选择之中，偏好在个人做出正确选择中的作用是不容易忽视的。一般认为，偏好是一种序关系，它是建立在行动主体所形成的认识状态、选择中相应情景规则以及相关主体倾向(情感、意愿等)的基础上的。因实际选择情景的需要，人们通常用两个二元关系来表达行动主体的偏好:严格偏好关系、无差异关系，以这两种关系为二元组形成一般性偏好关系或偏好结构，该偏好结构满足传递性和完全性，且有非循环性的要求。

然而，Luce等人［2－3］的研究却对选择理论的这一直观性假定构成了挑战，无差异偏好关系不具有传递性，进而可以推导出一般性偏好结构也不具有严格意义上的传递性。其他一些经济学家则表达了这样一种观点，实际选择情景中，行动主体的偏好可能不是传递的，准传递性［4－5］会更有利于选择的做出。实验社会选择理论通过具体选择实验，结果表明，即便是行动主体的偏好是严格的偏好关系，也会出现意想不到的选择结果，这构成对偏好结构直观特性的挑战。在群体选择理论的研究中，Condorcet［6］早就向人们揭示这样一种事实，由于偏好关系循环性的不可避免性，选择中个体的理性导致集体的非理性也是常有之事。Wang［7］曾提出了基于偏好循环的选择做出的程序化方法，但这一方法只是权宜之计，一种特殊的独裁［8］会在选择中出现，间接地违反了Arrow［9］对选择理论的基本假定。

一些经济学家或选择理论专家在这一问题上做出了不同程度的妥协或让步，主张传递性假定在实际选择中并非总是合理的［10－11］，尽管在理论中要求是这样。为使选择能够做出，应当放松对偏好某些性质的要求，可以允许与理论不符的偏好关系，例如有限的循环。［12］

但是这种妥协或让步，会使得选择的做出变得不可捉摸，远离理性的基础，可能会动摇选择理论的基本架构。因此，为确保理性因素、理性原则在选择中体现出应有的作用与价值，对偏好关系一般性质做进一步的、符合选择实际的考察，以此解决困惑选择理论的选择难题，显得尤为迫切。

1 社会选择中的分布式偏好

1.1 分布式偏好的形式刻画

分布式偏好［13］这一概念的提出源自于公共知识理论［14－16］中的分布式知识的思想，分布式知识的获取来自于不同成员的知识，而非单一的行动主体，即以他们知识的合取作为前提，推导出一些新的知识。由于这种知识源自不同的分布，故被称为分布式知识。基于此，我们进行新的拓展，把分布式偏好看作是某个或某些行动主体偏好的自然推导，因为它来自于不同的行动主体或同一行动主体的不同偏好，进一步地，对于传统意义上的传递性给予新的定义是必要的。

X={x1，x2，…，xn}为一选择方案集，G={1，2，…，n}为一群体，R为G的偏好关系(P、I为R结构的二元组元素)，C{X}={xi}，iN为选择函数。通过对相应符号标下标，我们可以对单主体的选择做出符号规定，则分布式偏好有如下两种形式上的定义:

定义 1.1 分布式偏好 RD:x1，x2，x3X，若x1Rx2且 x2Rx3，则 x1RDx3;［12］

定义 1.2 分布式偏好 RiD:x1，x2，x3X，若x1Rix2且 x2Rix3，则 x1RiDx3;［12］

根据上面定义，进一步地，可以把R做P或I的替换，对分布式偏好进行具体化表达或刻画。从本质上来讲，这一定义是传统选择理论的传递性定义，这正是需要改进的地方，传递性的定义将不同于传统的传递性。

RD和RiD及其相应的具体化均满足传统选择理论的一般性、完全性以及传统意义上的传递性，相应地，一些公理与定理显然成立。［13］

直观上讲，下列各式亦显然成立:［13］

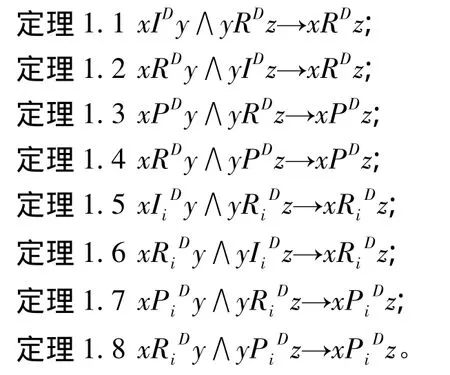
很显然，分布式偏好(关系)是经典选择理论偏好关系的传递性的一种表达，它产生的基本条件是方案集中的方案数目至少是3个。否则，无法满足传统意义上传递性的推导，方案间关系是一般意义上计算的结果，分布式偏好不可能出现。

基于分布式偏好，对传递性做出如下定义:

定义 1.3 x1，x2，x3X，若 x1Rx2，x2Rx3，且x1Rx3，则R是传递的。

定义 1.4 x1，x2，x3X，若 x1Rix2，x2Rix3，且x1Rix3，则 Ri是传递的。

可以看出，这是一种严格的传递性，基本条件是，x1或 x3满足 RD(RiD)和 R(Ri)，原因在于，x1Rx2与x2Rx3的结果是分布式偏好，即x1RDx3，而x1Rx3则是行动主体对关系的表达，即是显示性偏好。因此，RD(RiD)和R(Ri)共同决定了具有传递性，或者说行动主体基于x1、x2、x3所建构的偏好是传递的。

这里，对传递性的严格刻画，意在表明分布式偏好架构下的传递性不同于传统选择理论中的传递性，而不意味着选择的做出一定根据该严格的传递性进行，因为我们在基于分布式偏好的选择理论［12］中给出了选择的一些条件和规则。

1.2 基于分布式偏好的社会选择

根据上述定理，基于分布式偏好定义、传统选择理论偏好的一般性质以及传递性的特性，有下式成立:［13］

无论选择中，行动主体的偏好是经典偏好关系，或是分布式偏好关系，或是二者同时具有，依据上述各式进行推导，能够确定选择做出的偏好关系。

针对 Luce［2－3］给出的反例，基于我们所提出并刻画的分布偏好思想，我们认为，对于反例中行动主体而言，他所形成的让我们感到怪异的偏好是分布式偏好，而非表示性偏好(expressed preference)。正是由于二者的不一致或矛盾关系，导致与选择理论不符的吊诡现象出现。

在类似的情景中，起决定性作用(decisive)的是表示性偏好，传统意义上的传递性或分布式偏好没有起到任何作用，它只是对选择中的这一反常给出了警示。

然而，在大多数情况下，表示性偏好与分布式偏好是一致的，这时选择理论并没有表现出选择上的危机感。

在前期的研究［13］中，我们给出了R与RD间的多种可能的关系:一致、反一致、准一致、不可断定、弱反一致，并根据具体的选择实际，针对R与RD间具体关系，提出了选择的一般性规则。

不难看出，在行动主体的具体选择中，表示性偏好具有非同一般的重要作用和选择价值，分布式偏好只是选择过程的一个基本的参照系，如果某一偏好直接涉及选择，且它是表示性偏好而非分布式偏好，做出选择具有无疑的确定性;而选择中表示性偏好的缺失，也会使分布式偏好具有做出选择的决定性作用。只有当行动主体没有形成表示性偏好时，分布式偏好的选择作用才能得以发挥出来。在分布式偏好架构下，传递性同时满足分布式偏好与表示性偏好的结果，它是一种极其严格的表达与刻画。无论偏好关系是序关系的一种表达，还是基于广义效用计算基础的期望效用的基数关系［17－19］，选择中分布式偏好概念及思想的引入，能够对选择困难或悖论做出合理解释，并能够做出理性的选择。

2 分布偏好与Luce-Suppes难题的消解

2.1 Luce-Suppes难题

Luce-Suppes难题是 Luce、Suppes等人［20－23］提出来的，意在表明传统选择理论中的传递性并非是完美的，行动主体的偏好关系在许多情形下会表现出非传递性的特征。该难题的基本表述如下:

如果提供苹果(a)和香蕉(b)给一行动主体，让他根据自己的偏好做出选择，这时该行动主体会选择苹果，即他更偏好(爱)苹果;如果提供香蕉和樱桃(c)给该行动主体，让其选择，则该行动主体依据其对水果口味的偏爱，他会反而选择香蕉。现在的问题是，如果我们提供苹果和樱桃给该行动主体，他会做出什么选择呢?很自然地，我们都会认为，如果该行动主体是理性的，他应当会选择苹果。然而，事实上，他却选择了樱桃。

根据传统选择理论的传递性，该项行动主体在苹果、香蕉间以及香蕉、樱桃间做出选择的行为表明，他对于这些水果间的偏好关系应当这样来表达，即aPb和bPc，传统传递性应当使得这两个偏好关系的合取推导出一个新偏好来，即aPc，这一推导过程像3大于2、2大于1能够得出3大于1的结论，并且是不容质疑的。但是该行动主体并没有在苹果与樱桃中选择苹果，而是出人意料地选择了樱桃。

但是，行动主体的偏好是否像“大于”这类序关系那样，也是一种序关系呢?如果答案是肯定的，那么行动主体在选择中肯定是非理性的，但是在现实生活中，行动主体在这种极其简单的选择中表现出非理性确实是让人匪夷所思的，即使在理论的架构下，传递性也不可避免地会遭受质疑，如Luce 等人［2－3］的研究。①如果答案是否定的，那么，行动主体的选择依据怎样的规则才能体现出理性的特质来?

2.2 难题的消解:基于分布式偏好的方法

分布式偏好是来自行动主体对不同方案或事物②所形成的偏好，这一名称的来源在于，它是分布于其他偏好中所形成的偏好，而非直接得自于行动主体对方案或事物间关系的表达。它不同于传统选择理论的要点在于，选择时，行动主体的选择规则发生了变化，如果一行动主体仅仅具有分布式偏好，那么其选择的做出就仅仅依赖于该分布式偏好;而如果行动主体关于某两事物，即存在分布式偏好，也存在表示性偏好，那么表示性偏好将在选择中具有决定性的作用。

以Luce-Suppes对传统理论进行挑战提出的难题为例，对于选择中的行动主体而言，他所形成的偏好有:(1)苹果、香蕉间的偏好关系，aPb;(2)香蕉、樱桃间的偏好关系，bPc。这是直接为我们所看到的，也是我们认为该行动主体接下来会在苹果、樱桃间做出选择苹果的理由，因为基于传统选择理论的规则，这是必然的。

那么基于这两个偏好关系，关于苹果、樱桃间的偏好关系，他能够建立起分布式偏好关系aPDc。事实上，该分布式偏好仅仅是在行动主体的表达性偏好(cPa)缺失或不在场时，发挥独特的选择规则作用。当然，表达性偏好aPc的存在，并不影响行动主体的选择，因为无论根据哪一种偏好关系，行动主体的选择均是a，即苹果。

而此时，在行动主体那里，确实是存在cPa，故而，当我们提供苹果、樱桃给行动主体，让他做出二选一的选择时，让传统的选择理论者意外的是，他选择了c，即在苹果与樱桃之间，樱桃是他的偏好(爱)。也就是说，对于该行动主体来讲，既aPDc，也有cPa，在分布式理论架构下，cPa是具有决定性的，因此，aPDc便不具有任何的作用了。

2.3 简要评论

从分布式偏好理论不难看出，由于表达性偏好是行动主体基于两个方案或事物所直接形成的偏好，它是行动主体的一种直接建构，是一独立的陈述命题，也可以看作是因行动主体认知而形成的信念，而非推导的结果，因此，表达性偏好在选择中是极其重要的。

当然，表达性偏好并非总是存在的，在行动主体那里，许多的偏好关系来自于推导，形成的是分布式偏好。如果行动主体仅仅能够形成分布式偏好，那么这种偏好关系在选择中的作用等同于表达性偏好的作用，这其实是传统选择理论的观点，尽管该理论并没有作出表达性偏好与分布式偏好的区分。

通过前面的分析，不难看出，行动主体在做出选择时，他所形成的偏好并不是一种序关系，如果是一种序关系，那么对于相同的两个方案或事物而言，分布式偏好和表达性偏好是相同的，则分布式偏好就没有存在的必要了。

此外，分布偏好的建构，并没有削弱传统选择理论的选择效力，反而加强了行动主体选择做出的能力。这一点体现在，分布式偏好不仅仅能够解决Luce-Suppes难题，而且对于含糖咖啡这一选择理论的无差异性偏好关系的反例的解释来讲，也是功能强大的。

3 结语

无论是在经济选择中，还是社会选择中，对行动主体偏好关系传递性的要求是一个必要的特质，这一点容易产生的问题便是偏好的循环性。③进而在非严格的意义上，必定也要求无差异性偏好关系、不可决定性偏好关系应当是具有非循环特征的。只有当行动主体的偏好是建立在偏好关系的非循环性基础上，选择才能够顺利做出。

传统选择理论中，偏好关系无论基于序关系或是效用理论，在某种特殊选择情景中，都会给选择的做出带来一定的难度，如 Luce［2］以及 Luce与Raiffa［3］的例子都表明，因行动主体偏好关系而推导出的新的偏好关系只是选择做出的其中一个基本判据，如果不存在其他因素，这一判据会直接发挥选择的应有作用，而其他偏好关系因素的出现会使得这一判据“无用武之地”。因此，传统传递性在选择理论中可能是不足道的，选择的做出依赖于行动主体对效用的计算，而并非完全基于偏好关系的传递性，而这也能够足以解释选择中行动主体偏好逆转现象的出现。

分布式偏好是试图解决选择中循环性问题而提出的一种概念或思想，它使得选择的做出具有了更为明确的规则，并且很好地解释了选择中偏好逆转现象。

Luce-Suppes难题是选择理论中对传统选择理论传递性构成挑战的一个经典案例，它旨在表明，行动主体在偏好出现循环的情况下依旧能够做出选择，而并非仅仅是质疑了偏好关系的传递性。然而，这二者恰恰说明了传统选择理论中偏好关系存在的不足，也潜藏着一种新的解决这一不足的方法的可能性，这正是分布式偏好所要进行的工作。

不过，从我们给出的分布式偏好的定义、公理、定理以及选择条件出发，相对于传统理论而言，我们的工作迈出了本质性的一步，但可能因对行动主体偏好传递性给出的过于严格的定义，会增添选择的复杂度。此外，理论中析出函数在选择中的建构，对于不同的行动主体来讲，也会见仁见智。这些不足之处，会弱化分布式偏好在选择理论中的地位。

注 释:

① 该研究表明，无差异性偏好关系的传递性也会导致选择的困境，如桌子放着一杯无糖咖啡，即假定没有任何程度的含糖量，如果我们把一粒糖放入该咖啡中，那么我们会认为甜度没有发生变化。反复地做放入一粒糖的动作，我们都会感觉到咖啡的甜度与上次放入一粒糖的甜度是相同的。如果是这样，那么，放入次数到了一定的值，我们会因传递性而推导出，没有放糖的咖啡与放入一定数量如一百万粒糖的咖啡在甜度上是相同的。这足以使无差异性偏好关系的传递性在传统选择理论中瓦解掉。

② 一般来讲，这种偏好是行动主体通过3个方案或事物所形成的2个偏好所建构的。在所形成的2个偏好中，有1个方案或事物为中项，使得另外2个方案事物能够通过非直接性表达而建立起偏好关系，这一偏好关系就是分布式偏好，意思是指分布于另外2个偏好中所形成的。这类似于我们推理中的连锁推理，可以把建构分布式偏好关系的方法加以推广，进一步建构分布式偏好关系，即分布式偏好关系与另一有共同方案或事物的偏好关系，能够建构新的分布式偏好关系。

③ 这里的循环性主要是针对严格偏好的传递性而言的，行动主体偏好中循环的出现意味着选择的无法决断，继而在选择面前犹豫不定。然而，在严格意义上，无差异性偏好关系以及不可判定性偏好关系是允许循环的，如a与b是无关的，b与c是无差异的，那么a与c也是无差异的，这一推导的结论无疑地能够被行动主体接受，但他也能够接受c和a是无差异的这一结论。因此严格偏好关系产生的循环是“恶”循环，而无差异性偏好关系、不可决定性偏好关系所产生的循环是“良”循环，因为前者影响了行动主体选择的做出，而后者则没有。

［1］Fishburn P C.Utility Theory for Decision Making［M］.Malabar:Robert E.Krieger Publishing Company，1979:15.

［2］Luce R D.Semiorders and a Theory of Utility Discrimination［J］.Econometrica，1956(24):178－191.

［3］Luce R D，Raiffa H.Games and Decisions［M］.New York:Wiley，1957:61 －68.

［4］Armstrong W E.Utility and the Theory of Welfare［J］.Oxford Economic Papers，1951(3):259 －271.

［5］Weinstein A A.Individual Preference Intransitivity［J］.Southern Economic Journal，1968(34):335 －343.

［6］Condorcet M de.Essai sur LApplication de LAnalyse à la Probabilité des Decisions Rendues à la Pluralité des Voix［M］.Paris:De Limprimerie Royale，1785.

［7］Wang Z Y.Existence of Satisfied Alternative and the Occurring of Morph-Dictator［C］//Xiandong H，John H，Eric P.Proceedings of Second Logic，Rationality，and Interaction.Heidelberg:Springer-Verlag，2009:327－328.

［8］王志远.TESA及其在孔多塞选择中的应用［J］.天津商业大学学报，2010(1):51－55.

［9］Arrow K J.Social Choice and Individual Values［M］.New York:Wiley，1963:2－5.

［10］May K O.Intransitivity，Utility and the Aggregation of Preference Patterns［J］.Econometrica，1954(22):1 －3.

［11］Tversky A.Intransitivity of Preferences［J］.Psychology Review，1969(76):31－48.

［12］Schwartz T.Rationality and the Myth of the Maximum ［J］.No^us，1972(2):97 －117.

［13］王志远.分布式偏好及其在选择中的作用［J］.河南社会科学，2010(4):93－96.

［14］van der Hoek W，Meyer J J Ch.Group Knowledge is not Always Distributed(Neither is it Always Implicit)［J］.Mathematical Social Sciences，1999(38):215 －240.

［15］Gerbrandy J.Bisimulations on Planet Kripke［D］.Amsterdam:University of Amsterdam，1999.

［16］Roelofsen F.Distributed Knowledge［J］.Journal of Non-classical Logics，2006(16):1－16.

［17］Von Neumann J，Morgenstern O.Theory of Games and Economic Behavior［M］.Princeton:Princeton University Press，1944:55.

［18］Savage L J.The Foundations of Statistics［M］.New York:Wiley，1954:67.

［19］王志远.模糊偏好的形成机制研究［D］.南京:南京大学，2010:67－71.

［20］Luce R D，Suppes P.Preference，Utility and Subjective Probability［C］//Luce R D，Bush R R，Galanter E.Handbook of Mathematical Psychology:Vol.3.New York:John Wiley and Sons，1965:249 －410.

［21］Suppes P，Krantz D H，Luce R D，et al.Foundations of Measurement:Geometrical，Threshold，and Probabilistic Representations［M］.New York:Academic Press，1989.

［22］Scott D，Suppes P.Foundational Aspects of Theories of Measurement［J］.The Journal of Symbolic Logic，1958(23):113－128.

［23］Luce R D.Individual Choice Behavior:A Theoretical Analysis［M］.New York:John Wiley and Sons，1959.