涉及微分多项式的亚纯函数族的正规性

李三华，罗节英

涉及微分多项式的亚纯函数族的正规性

*李三华，罗节英

(井冈山大学数理学院，江西，吉安 343009)

在给定的条件下，讨论亚纯函数正规族与其微分多项式之间关系。

亚纯函数；零点；微分多项式；正规族

0 引言

平面区域内的一族亚纯函数在内正规,如果内的任一函数列都含有在内按球距内闭一致收敛的子列。

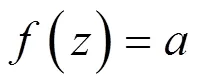
方明亮和L.Zalcman在文献[1]中证明了下面的结果：

在本文中，我们证明了：

1 引理

2 定理1的证明

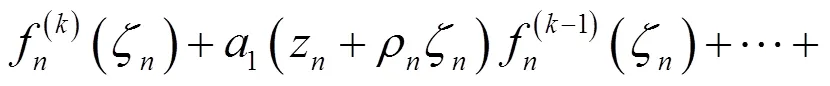
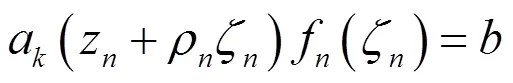
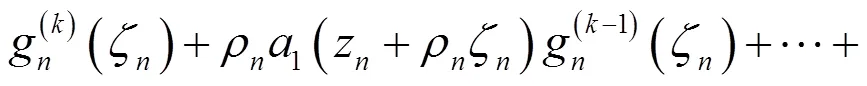
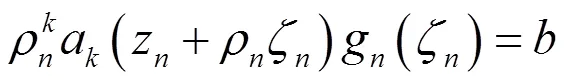
下面证明：

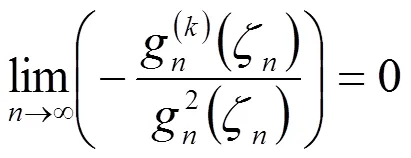
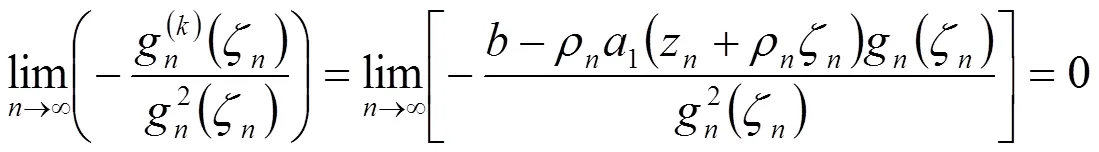
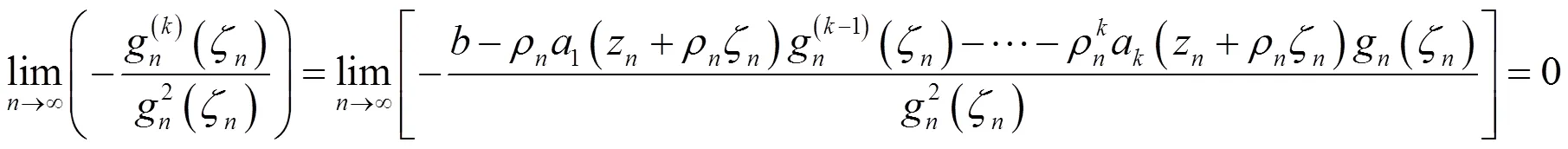
由数学归纳可知(2.2)成立。

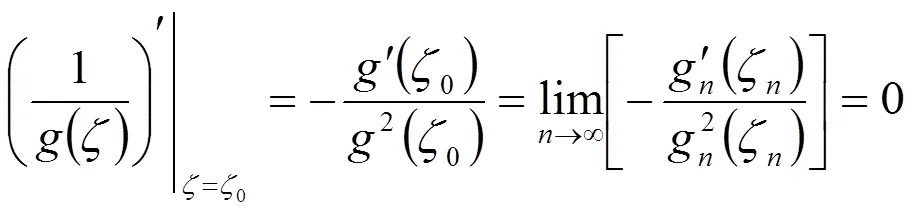
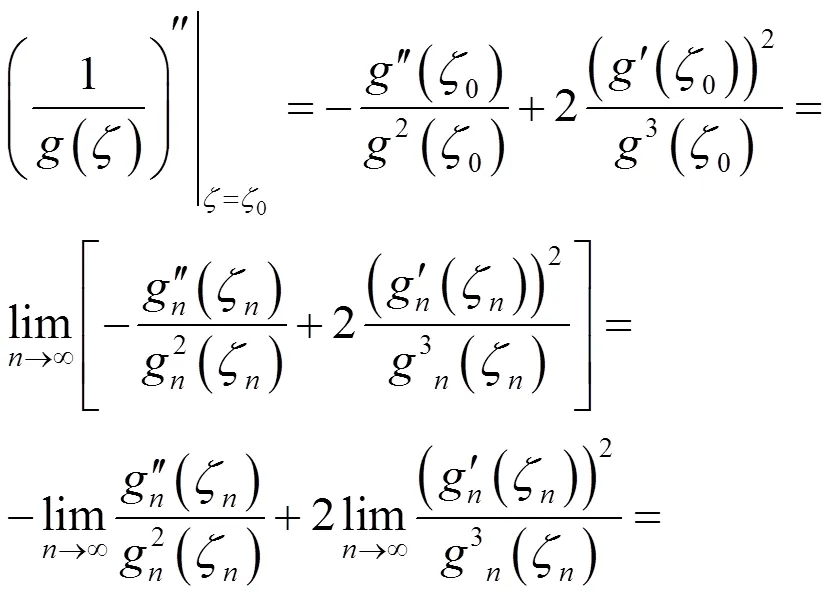
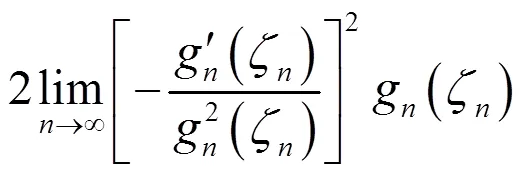
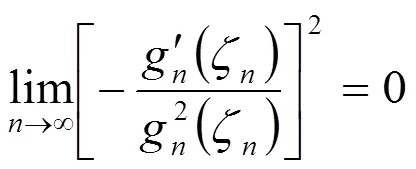
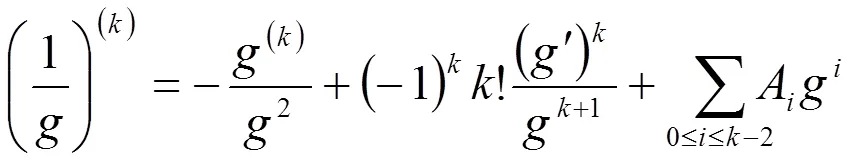
因此由(2.1)和(2.5)得

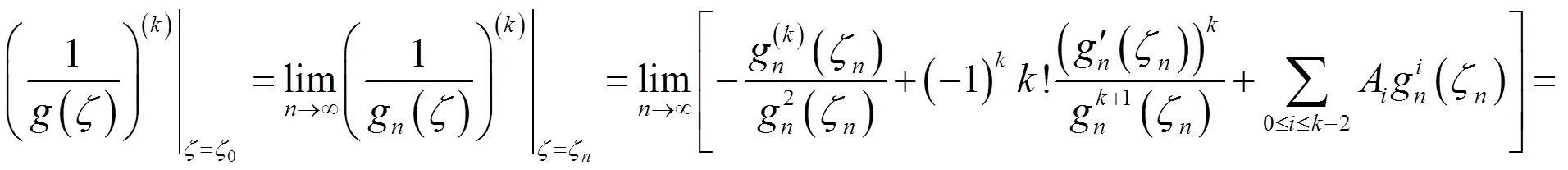
(2.6)

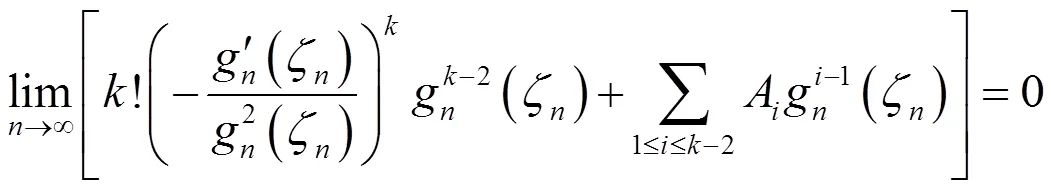
类似地可得

如此进行下去，归纳可得

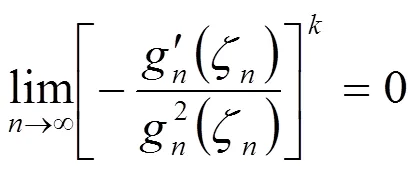
由引理 3 知，是有理函数。若是多项式,则由的零点重级至少为+1及(1)可知，是常数, 矛盾；若是非多项式有理函数，则由的零点重级至少为+1，(1)以及引理4可知，有一单级极点，与没有单级极点矛盾。

[1] Fang MingLiang, Zalcman L. Normal families and shared values of meromorphic function III [J]. Comput Methods Funct Theory, 2002, 2(2): 385-395.

[2] Pang XueCheng, Zalcman L. Normal families and shared values [J]. Bull London Math Soc, 2000, 32: 325-331.

[3] Clunie J, Hayman W K. The spherical derivative of integral and meromorphic functions [J]. Comment Math Helvet, 1966, 40: 117-148.

[4] 顾永兴,庞学诚,方明亮. 正规族理论及其应用[M]. 北京: 科学出版社, 2007.

[5] 李三华.分担一个全纯函数的亚纯函数族与正规性[J].华东师范大学学报, 2011,(2): 54-61.

Normal families associated with differential polynomial

*LI San-hua, LUO Jie-ying

(School of Mathematics, Jinggangshan University, Ji’an, Jiangxi 343009, China)

We discuss the normal families of meromorphic functions associated with its differential polynomial in given conditions.

meromorphic function; Zero point; differential polynomial; normal families

O174.52

A

10.3969/j.issn.1674-8085.2012.02.005

1674-8085(2012)02-0019-03

2012-01-05；

2012-02-23

井冈山大学科研基金项目(JZ11002)

*李三华(1982-)，女，江西吉安人，讲师，主要从事复分析研究(E-mail: lisanhua@sina.com)

罗节英(1979-)，女，江西吉安人，讲师，主要从事数学课程研究(E-mail:webshiplxj@126.com).