固定接触界面法向静弹性刚度的改进弹簧分形模型

田红亮 朱大林 秦红玲

（三峡大学 机械与材料学院，湖北 宜昌 443002）

结合材料是利用某种结合方法（如螺栓、双头螺柱、螺钉、紧定螺钉、键、花键、销、铆钉、榫齿连接等）把两种不同或者相同的材料连接在一起使用的结构或组合材料，而结合材料的结合部统称为界面［1］，界面占机床总柔度的60%.随着各类功能材料、复合材料等先进材料的工业应用范围的不断扩大，由不同材料组成的界面的力学行为，越来越受到人们的重视.一方面在宏观范围内，各类结构及材料的结合部，如薄膜涂层材料的涂层界面、金属／陶瓷结合界面、异种金属结合界面、功能器件与承载构件的结合界面、复合材料层合板的层间等，对材料或结构整体的力学行为乃至其功能性能有着十分重要甚至是支配性的影响；另一方面在细观范围内，纤维与基体材料等的界面、晶粒界面、颗粒增强体与基体的界面、介在物与基体的界面等的力学行为，对先进材料的性能设计与开发及其结构寿命的精确评价等，具有举足轻重的意义.界面问题有它许多自身固有的特性，现实生活中总在自觉或不自觉地利用界面的特性.例如，利用粘接界面的抗剥离能力较弱的特性，来设计包装的封口，或引入复合材料中的桥联增韧机构等.然而，在新材料和新结构的设计开发中，则一般要求界面强度达到一定的要求，甚至为了提高界面强度，而不断进行结合方法、工艺和界面结构的革新.20世纪末，许多更为可靠和有效的结合手段应运而生，如扩散结合、锡焊、激光焊接等，使得结合界面更为精致，甚至出现了结合部位的强度超过被结合的母材的情况.由于界面层一般很薄，通常在几微米，大至数百个微米的量级，因此界面没有厚度，却有自身固有的强度特性、弹性特性.界面有3类：完全结合界面、剥离界面、接触界面.其中接触界面有2类：固定接触界面、滑移接触界面.

以线性或非线性的弹簧，来表征双材料结合部的相互约束，即为界面的弹簧模型.通过引入法向和切向的弹簧，必要时甚至可以引入相应的阻尼，理论上应该可以描述界面层材料对界面两侧材料的约束作用.弹簧模型的特点是，界面处的面力是连续的，而位移则通常有一个落差，是不连续的，这种模型较适宜于描述结合相对较软的界面.山田昭夫和角张毅［2］引入GW模型［3］从理论上研究了接触面全体的法向刚度、切向刚度.Burdekin等［4］给出了机床结合部变形量－界面名义接触压应力方程.Thornley等［5］给出了机床结合部平均界面压应力－法向变形量的加载、卸载曲线.Gao等［6－7］给出了单峰法向、切向弹性刚度的解析解.张学良等［8］引用 MB模型［9］首次提出粗糙表面的法向接触刚度.

本文根据Hertz接触理论推导两个微凸体间互相作用的法向接触静弹性刚度.利用改进分形几何理论给出结合部的总法向接触静弹性条件刚度、总条件载荷的解析解.依靠文献［10］的机床结合部变形量－界面压应力的经验幂律关系形式，推导界面静弹性刚度、总载荷.

1 分形几何理论的改进

Weierstrass－Mandelbrot函数能模拟一个表面轮廓的几何形貌，根据 Weierstrass－Mandelbrot函数能够计算一个单峰顶端的变形量，法向弹性载荷与一个单峰顶端的变形量、分形维数D、分形粗糙度G等参数有关，故法向弹性载荷与 Weierstrass－Mandelbrot函数间接有一定的联系.处处连续、统计学自相似性、点点不可微的Weierstrass－Mandelbrot函数为

式中，X为表面上高度是Z的一点的平面直角坐标；L为取样长度；G为分形粗糙度；D为表面轮廓的分形维数；γ为与表面轮廓频谱密度相关的参数.

引入以下3个无量纲参数

式（1）可改写为

考虑工程粗糙表面的最低频率，式（5）可改写为

式中，n1为最低频率的初始项.

需要强调的是：式（6）是严格的无量纲形式，式（6）与文献的式（1）有本质区别，式（6）中的γn无量纲，文献中γn的量纲是 m－1.

当g＝0.01，γ＝1.5，n1＝1，n＝n1～100时，式（6）表达不同分形维数的表面轮廓高度如图1所示.

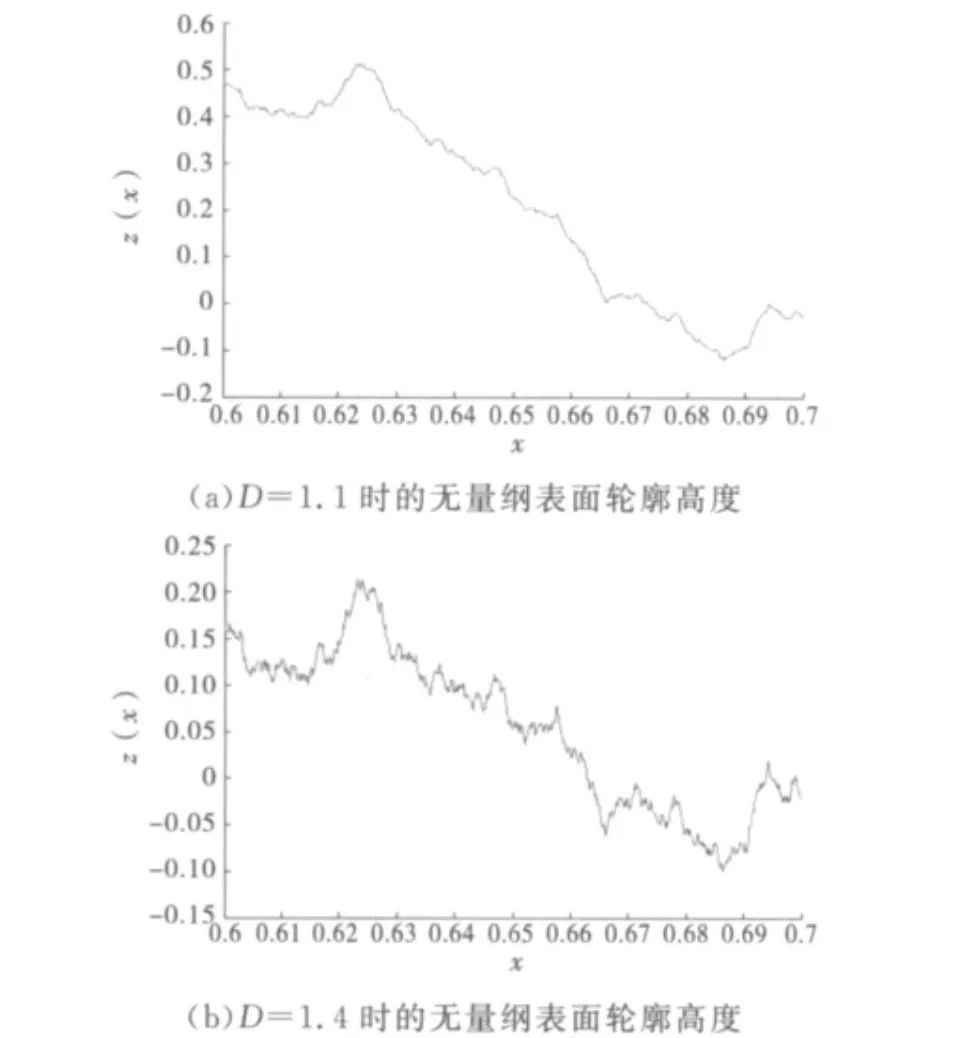
图1 不同分形维数的无量纲表面轮廓高度

依照式（1），一个单峰顶端的变形量由 Weierstrass－Mandelbrot分形函数决定，取决于余弦函数的波峰和波谷的幅值（即谐波分量的系数）［9］，故一个单峰顶端的变形量为

式中，a为一个接触点的面积，且

赫兹的峰顶曲率半径为

值得一提的是：式（9）不同于文献［9］的式（7）.

式中，K＝H／σy，H 为硬度，0.5≤K≤3；σy为较软材料的屈服强度；φ＝σy／E′为材料特性.

值得指出的是：式（10）也不同于文献［9］的式（9）.

式（7）／式（10），得

式中，ac为划分弹塑性区域的临界面积，且

需要指出的是：式（12）亦不同于文献［9］的式（10）.

一个接触点面积a的尺寸分布为

式中，aL为最大的接触点面积.

面积在a与a＋da之间的接触点数是n（a）da，故实际接触面积为

单峰承受垂直于界面的法向弹性载荷为

需要指出的是：式（15）亦不同于文献［8］的式（1）.将式（9）的第一部分δ＝代入式（15）得

将式（9）代入式（16）得

值得一提的是：式（17）亦不同于文献［9］的式（14）.

单峰承受的法向塑性载荷为

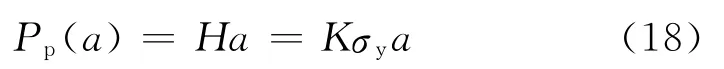
当aL＞ac时，总法向载荷为

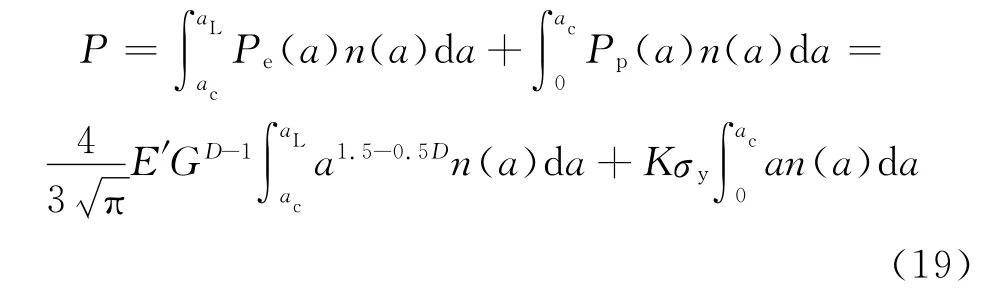
根据L＇Hospital法则，可得极限

将式（13）代入式（19）并顾及式（20）得

需要指出的是：式（21）也不同于文献［8］的式（15a）、式（15b）.由式（14）得

式中，Aa为表观接触面积；＝为接触率.

根据式（20）及式（22），可将式（21）化为无量纲形式

需要指出的是：式（23）也不同于文献［11］的式（11）.

2 固定接触界面的法向静弹性刚度

由式（15）可得函数Pe（δ）对自变量δ的导数为

必须明确的是：在两个微凸体间互相作用的法向接触静弹性刚度kn不能按照文献［12］提供的“集中载荷除以挠度”方法

可以看出，式（24）中的系数“2”不同于式（25）中的系数“4／3”.

将式（9）的变形式a＝πRδ代入式（24）得

根据式（26），可得整个界面的总法向刚度为

将式（13）代入式（27）且鉴于式（20）得

根据式（20）暨式（22），可将式（28）化为无量纲形式

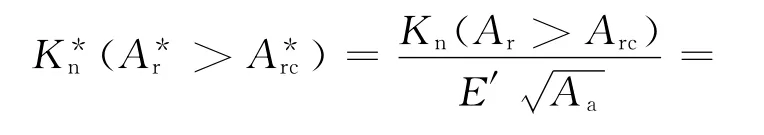
值得指出的是：文献［13］中的函数g3（D）＝应为

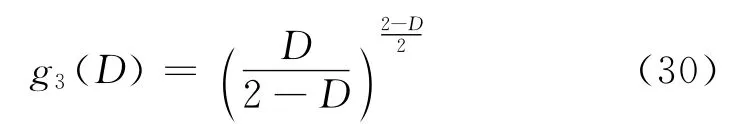
根据式（23），P＊是（图2）的显函数，一般的，用对应关系P＊＝φ（）表达.同理根据式（29），也是的显函数，用＝ψ（）表示.因此，通过中间变量可确定与P＊间的参数方程

故自变量P＊和因变量确定了一个隐函数

图2 工程粗糙表面的实际接触面积

3 工程粗糙表面实例与实验比较

当K＝1，G＊＝10－10，D＝1.5，最小材料特性、总法向接触刚度如图3所示.由图3（a）可知最小有效材料特性为2.641×10－5.

图3 最小有效材料特性、总法向接触刚度

当K＝1，φ＝10－2，D＝1.9，最大有效分形粗糙度、总法向接触刚度如图4所示.按照图4（a）可获得最大有效分形粗糙度为0.000 38.

图4 最大有效分形粗糙度、总法向接触刚度

当K＝0.5，φ＝10－2，G＊＝10－10，最小有效分形维数、总法向接触刚度如图5所示.由图5（a）可得到最小有效分形维数为1.251.

图5 最小有效分形维数、总法向接触刚度

文献［10］通过位移传感器测量35个圆环体的法向、切向变形量，给出机床结合部变形量－界面压应力的经验幂律关系形式

式中，λn为法向变形量，单位是（μm）；pn为表观法向压应力，单位是（Pa）；对研磨－手动刮抛光表面，C＝0.001 3，m＝0.46；对研磨－研磨抛光表面，C＝0.001 4，m＝0.5.

由式（33）得

界面法向静弹性刚度为

式（36）、界面总载荷的无量纲形式分别为

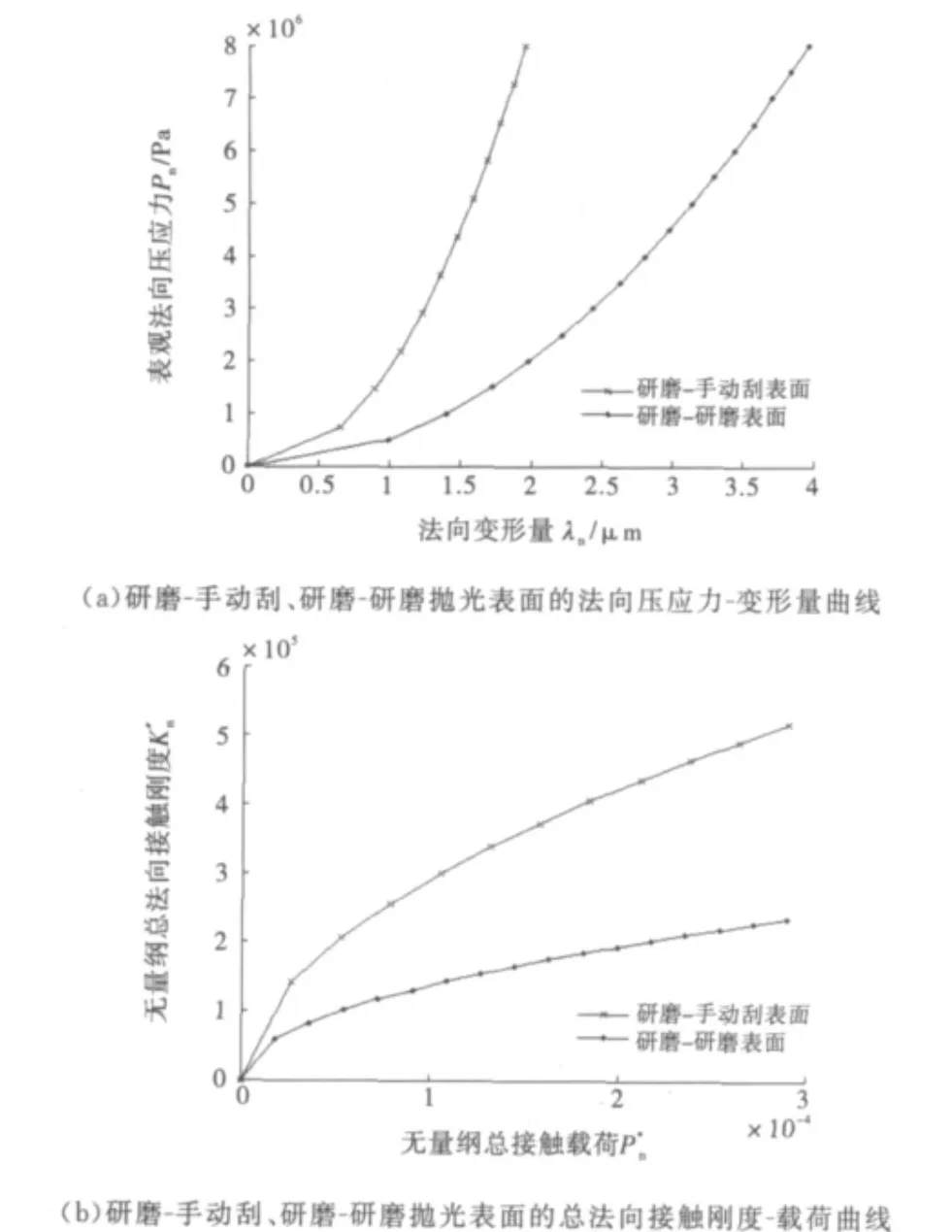
图6 文献［10］的实验法向压应力、法向刚度

通过上述数值仿真与实验比较，可得下列结论：①图3（b）、图4（b）、图5（b）都说明，总法向接触静弹性刚度线性地随总法向载荷增加而增加，这与图6（b）总法向刚度－载荷微凸弧曲线的实验结论基本一致.②图5（b）说明，总法向接触静弹性刚度随分形维数增加而增加，因为表面越粗糙，分形维数越小.③图4（b）显示，总法向接触静弹性刚度随分形粗糙度减小而增加，因为部分弹性接触面积随分形粗糙度增加而减小.④图3（b）论证，总法向接触静弹性刚度随材料特性增大而增大，因为材料特性越小，部分弹性接触面积减小.

4 结 论

根据Hertz接触理论推导两个微凸体之间互相作用的法向接触静弹性刚度.引用改进分形几何理论给出结合部的总法向接触静弹性条件刚度、总条件载荷的解析解.按文献［10］的机床结合部变形量－界面压应力的经验幂律关系形式，推导界面静弹性刚度、总载荷.工程粗糙表面的算例表明，本文的总法向刚度－载荷曲线与文献［10］的实验结论基本一致.

［1］ 许金泉.界面力学［M］.北京：科学出版社，2006：1.

［2］ 山田昭夫，角张毅.接触结合部をもつはりの动特性推定［J］.精密工学会志，1986，52（12）：2051－2057.

［3］ Greenwood J A，Williamson J B P.Contact of Nominally Flat Surfaces［J］.Proceedings of the Royal Society of London：Series A Mathematical and Physical Sciences，1966，295（1442）：300－319.

［4］ Burdekin M，Back N，Cowley A.Analysis of the Local Deformations in Machine Joints［J］.The Journal of Mechanical Engineering Science，1979，21（1）：25－32.

［5］ Thornley R H，Connolly R，Barash M M，et al.The Effect of Surface Topography Upon the Static Stiffness of Machine Tool Joints［J］.International Journal of Machine Tool Design ＆ Research，1965，5（1／2）：57－74.

［6］ Gao Y F，Lucas B N，Hay J C，et al.Nanoscale Incipient Asperity Sliding and Interface Micro－Slip Assessed by the Measurement of Tangential Contact Stiffness［J］.Scripta Materialia，2006，55（7）：653－656.

［7］ Gao Y F，Xu H T，Oliver W C，et al.Effective Elastic Modulus of Film－on－Substrate Systems under Normal and Tangential Contact［J］.Journal of the Mechanics and Physics of Solids，2008，56（2）：402－416.

［8］ 张学良，黄玉美，傅卫平，等.粗糙表面法向接触刚度的分形模型［J］.应用力学学报，2000，17（2）：31－35.

［9］ Majumdar A，Bhushan Bharat.Fractal Model of Elastic－Plastic Contact Between Rough Surfaces［J］.ASME Journal of Tribology，1991，113（1）：1－11.

［10］Burdekin M，Back N，Cowley A.Experimental Study of Normal and Shear Characteristics of Machined Surfaces in Contact［J］.The Journal of Mechanical Engineering Science，1978，20（3）：129－132.

［11］张学良，黄玉美，温淑华.结合面接触刚度分形模型研究［J］.农业机械学报，2000，31（4）：89－91.

［12］程耀东，李培玉.机械振动学［M］.2版.杭州：浙江大学出版社，2006：26.

［13］张学良，黄玉美，韩 颖.基于接触分形理论的机械结合面法向接触刚度模型［J］.中国机械工程，2000，11（7）：727－729.

［14］濮良贵，纪名刚.机械设计［M］.7版.北京：高等教育出版社，2003：412.