SOI纳米波导的优化制备与弯曲损耗测试*

臧俊斌，薛晨阳，韦丽萍，王景雪，崔丹凤，王永华，仝晓刚

(1.中北大学仪器科学与动态测试教育部重点实验室，太原 030051；2.中北大学电子测试技术国家重点实验室，太原 030051)

随着集成光学的迅猛发展，基于硅基光网络传输的微电子芯片突破了传统微处理器内部互联中带宽和能量的限制，成为未来光通信和光计算的主要发展方向。光波导作为集成光学的主要部件，在与激光器、调制器、放大器等光电器件［1－2］的光互联和光传输中起着至关重要的作用。由于光电子芯片发展的微型化和集成化促使光波导器件也必须朝着高集成度、微小型化的方向发展，所以实现光波导器件中的弯曲是必须的。波导的弯曲势必会产生弯曲损耗，如何实现并制备出超低弯曲损耗的纳米波导结构，成为人们广泛研究的热点。

高品质的硅基 SOI(Silicon-on-insulator)材料，由于其高的折射率差、通信波段的透明传输以及制作工艺与CMOS工艺完全兼容等优点成为研制纳米光波导的首选。但目前采用SOI材料直接刻蚀制备得到的波导结构其侧壁非常粗糙以至于损耗特别严重［3－5］，所以国外针对这一问题提出了采用H2退火处理来降低波导的侧壁粗糙度［6］。而国内由于工艺水平受限，只能试探性采用可替代的处理工艺来完成。因此，本文主要阐述了SOI纳米光波导的设计与制备，并结合国内MEMS工艺的可行性对纳米光波导的表面优化处理进行了研究，最后采用透射谱法对制备出的波导进行弯曲损耗测试。测试结果表明，优化处理后的环形波导的弯曲损耗提高了2倍。

1 光波导的设计与制备

1.1 光波导结构设计

为实现光波导超低损耗的光能量传输，必须要保证波导传输的单模性和高光场局域性［7－8］。因此需要对波导的整体结构进行理论分析，设计出最优的波导结构。本文采用Optiwave-FDTD和Rsoft对SOI硅基纳米光波导结构的单模性和高光场局域性进行了理论仿真分析。

当输入光波长为1.55 μm时，波导厚度为0.03 μm、0.15 μm、0.22 μm、0.27 μm 和0.273 μm 的 TE模态光场分布图如图1所示。由仿真结果可以看出，当波导层厚度小于0.03μm时，光场局域性很弱，光能量几乎全部外泄；当波导层厚度大于0.273 μm时，光场会出现0阶和1阶的双模态性，致使波导不再是单模态传输；当波导层厚度处于0.03 μm到0.273 μm时，波导为单模传输。但由于工艺条件的限制，几十纳米厚度的光波导结构很难在制备中得到控制；再结合波导模有效折射率的变化关系图(如图 2 所示)，波导厚度在 0.2 μm ～ 0.23 μm时，有效模折射率达到最大敏感值，因此我们选定波导层的厚度为 0.22 μm。

图1 不同波导层厚度对应的光场分布图

图2 有效模折射率随波导层厚度变化关系图

采用FDTD仿真分析得到了波导单模态传输特性下的最佳波导层厚度。图3为波导层厚度为0.22 μm、入射波长为 1.55 μm 时，采用 Rsoft仿真分析得到的TE模态下不同波导宽度对应的高光场局域能力图。由图可以清晰看出当波导宽度为0.45 μm时，中心红色区域最亮、最集中，及光场的局域性最好。基于以上仿真分析结果，确定了SOI硅基光波导的结构如图4所示(波导厚度h=0.22 μm，宽度d=0.45 μm)。

图3 不同波导宽度对应的波导截面局光强度分布图

图4 SOI硅基光波导结构截面图

1.2 光波导制备

本文主要采用电子束光刻(Electron Beam Lithography)、ICP刻蚀、高温退火、BOE湿法腐蚀等工艺对图4所示的光波导结构进行制备加工与优化［9－10］，其整个制备过程示于图 5。

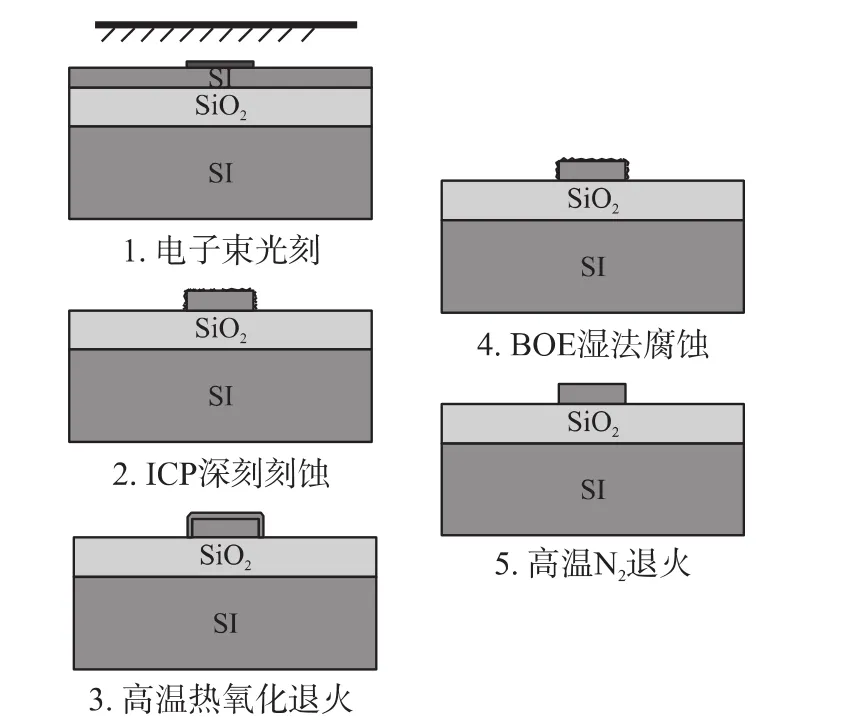
图5 光波导的制备和后处理流程

制备中采用的电子束光刻机为直写式JBX5500ZA，其制作的线条精度低于10nm；所用的ICP深硅刻蚀机为STS HRM，ICP刻蚀技术由于结合了化学、物理刻蚀方法的优点，不但可以获得好的刻蚀方向性和选择性，而且其刻蚀速度也得到了很大提高，使得最终制备的波导陡直度将达(89±1)°。此外，我们还进行了后期的表面结构优化处理，主要步骤为300℃到1 200℃热氧化退火、BOE湿法腐蚀以及1 000℃高温N2退火等。其中图6所示为885℃热氧化退火、BOE湿法腐蚀和1 000℃高温N2退火后的SEM图。

图6 处理后的环形波导SEM图(插图为侧壁SEM)

2 实验测试分析

基于§1.2中制备的纳米波导结构，采用Dimension3100原子力显微镜对波导的表面粗糙度进行测试，其垂直方向的最小测试范围小于0.05 nm。此外，由于透射谱测试法适用于纳米级尺寸光波导的损耗测试，且对环形波导谐振腔的测试误差较小［11］，所以本文拟采用透射谱测试法对光波导的弯曲损耗进行测试。

考虑到实际中对波导侧壁粗糙度进行测试的可行性，制备中采用未完全刻蚀的等效方法，用200 nm刻蚀深处的表面粗糙度来近视估测侧壁的粗糙度。Dimension3100的AFM测试结果如图7所示，由图可以看出波导的侧壁陡直度达89°(与理论值基本一致)。同理，由AFM测试得到了在不同热氧化退火温度下，经过BOE腐蚀和高温N2退火处理后对应的表面粗糙度实验值Ra，由Ra拟合得到的对应曲线示于图8。

图7 纳米波导结构的AFM测试图

图8 BOE腐蚀和高温N2退火后处理相同时Ra随热氧化退火温度变化曲线图

由图8可见，随着热氧化退火温度的增大，光波导的侧壁粗糙度Ra值在600℃以内基本保持不变，超过600℃后Ra值会先减小后又急剧增大，当退火温度处于900℃左右时Ra值达到最小。这是因为当温度低于600℃以下时，光波导表面未被氧化为SiO2，以至于后续的BOE腐蚀以及高温N2退火对其基本没有影响；而当温度处于600℃到900℃之间时，表面部分被氧化了，再加上BOE腐蚀和高温N2退火后最大化了表面晶粒尺寸使得表面粗糙度得以降低；但是当退火超过1 000℃后，由于波导基本被完全氧化为SiO2，致使波导发生形变以至于表面粗糙度又急剧增大。

由此，结合我们实际的波导结构和AFM的测试结果，采用透射功率法对弯曲损耗进行精确测定。其弯曲损耗计算可由下式得出:

上式中，是环形波导每周的功率损耗百分比，δλd是透射谱线的半高宽，rt是谐振峰对应的最低功率值，FSR是自由频谱宽度，以上各参量都可以在谐振透射谱线中得出。其中图9所示为未经过任何优化后处理的半径为15 μm环形波导通过示波器测试得到的透射功率图；图10为对应于图6环形波导的透射功率图(半径也为15 μm)。

图9 未优化处理得到的半径为15 μm的透射功率图

图10 对应图6优化处理后得到的半径为15 μm功率透射图

由图9和图10测试得到的环形波导透射功率谱可得到各自的 δλd、rt、FSR 值，再根据式(2)得到其对应的为 7.32×10－3和 2.502×10－3，代入式(1)即可得到半径为15 μm的环形波导优化处理前后的弯曲损耗 αbend分别为(0.032±0.001)dB/turn和(0.0109±0.001)dB/turn。进一步根据 Miller和Marcatili给出的解析式［12］:

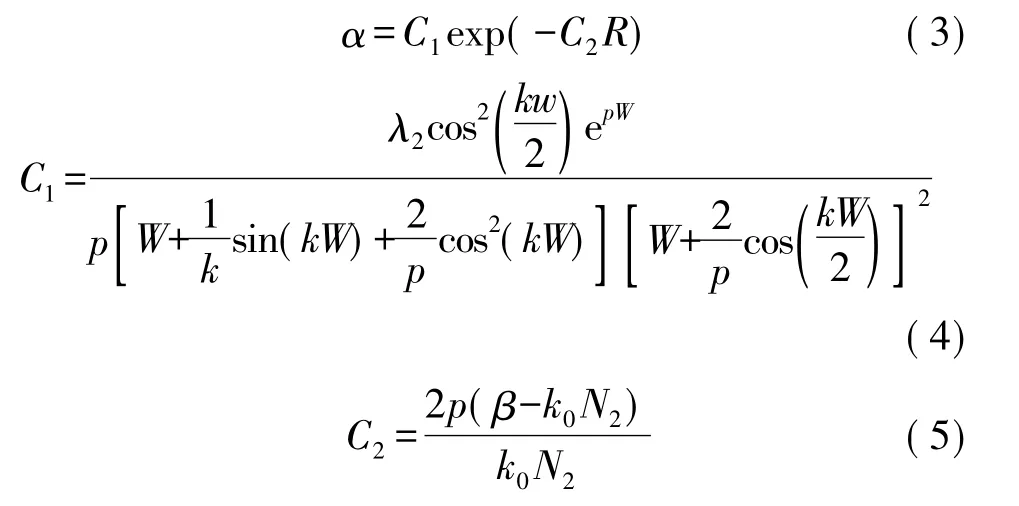
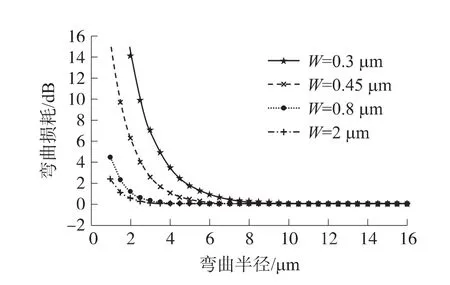
图11 弯曲损耗随弯曲半径变化关系图

由图11可见，环形波导的弯曲半径越大，则波导弯曲损耗越小；且当弯曲半径小于9 μm的情况下，弯曲损耗受弯曲半径的影响非常显著，将随着弯曲半径的增加而以指数形式迅速减小。当弯曲半径大于9 μm时，不同宽度环形波导的弯曲半径对弯曲损耗的影响不大，同理也验证了我们以上测试得到的半径为15 μm的环形波导弯曲损耗的合理性，同时也更进一步说明优化处理后的弯曲损耗更接近理论值。

3 结论

本文依据Optiwave-FDTD和Rsoft对纳米光波导的单模态性与高光场局域性的仿真分析结果，采用电子束光刻(Electron Beam Lithography)与ICP刻蚀制备得到了纳米光波导结构。进一步采用不同的后处理工艺对制备出的波导结构进行了优化后处理。又使用高精度原子粒显微镜对优化处理后的纳米波导结构进行表面粗糙度测试，并给出了表面粗糙度随热氧化退火温度变化的拟合曲线。在此基础上采用透射谱测试法对未优化处理的纳米波导结构和最小Ra值的纳米波导结构分别进行了弯曲损耗测试。结果表明:在BOE腐蚀和高温N2退火不变的情况下，随热氧化退火温度的增大，表面粗糙度Ra值呈先下降后又急剧增大的趋势；而且，在900℃附近时Ra值达到最小。此外，通过比较两组弯曲损耗的测试结果可知，半径为15 μm的纳米环形光波导经过885℃高温氧化退火、BOE腐蚀以及1 000℃高温N2退火后的弯曲损耗降低到(0.0109±0.001)dB/turn，其实验结果与理论值相一致。

［1］Wang P，Semenova Y，Farrell G.Temperature Dependence of Mac-robending Loss in All-Fiber Bend Loss Edge Filter［J］.Optics Communications，2008，281(17):4312－4316.

［2］武继江，石邦任，郭丽君.退火质子交换Y分支波导弯曲损耗分析［J］.传感技术学报，2006，19(3):786－789.

［3］Shijun Xiao，Maroof H Khan，Hao Shen，et al.Modeling and Measurement of Losses in Silicon-on-Insulator Resonators and Bends［J］.Optics Express，2007，15(17):10553－10561.

［4］Victoria Astley，Julianna Scheiman，Rajind Mendis，et al.Bending and Coupling Losses in Terahertz Wire Waveguides［J］.Optics Letter，2010，35(4):553－555.

［5］Shankar Kumar Selvaraja，Wim Bogaerts，Dries Van Thourhout.Loss Reductions in Silicon Nanophotonic Waveguide Micro-Bends Through Etch Profile Improvement［J］.Optics Communications，2011，284:2141－2144.

［6］Ling Liao，Desmond R Lim.Optical Transmission Losses in Polycrystalline Silicon Strip Waveguides:Effects of Waveguide Dimensions，Thermal Treatment，Hydrogen Passivation，and Wavelength［J］.Journal of Electronic Materials，2000，29(12):1380－1386.

［7］Zendehnam A，Mirzael M，Farashiani A，et al.Investigation of Bending Loss in a Single-Mode Optical Fibre［J］.Pramana-Journal of Physics，2010，74(4):591－603.

［8］Ngoc Hai Vu，In-Kag Hwang，Yong-Hee Lee.Bending Loss Analyses of Photonic Crystal Fibers Based on the Finite-Difference Time-Domain Method［J］.Optics Letters，2008，33(2):119－121.

［9］Jaime Cardenas，Carl B Poitras，Jacob T Robinson，et al.Low Loss Etchless Silicon Photonic Waveguides［J］.Optics Express，2009，(17)6:4752－4757.

［10］祝洪良，杨德仁，汪雷，等.氮气氛中高温热处理硅片表面的直接氮化［J］.半导体学报，2003，24(10):1049－1052.

［11］Shaowu Chen，Qingfeng Yan，Qingyang Xu，et al.Optical Waveguide Propagation Loss Measurement using Multiple Reflections Method［J］.Optics Communications，2005，256(1－3):68－72.

［12］Marcatili E A J，Miller S E.Improved Relations Decribing Directional Control in Lectromagnetic Wave Guidence［J］.Bell Syst Tech J，1969，48(9):2161－2188.