广义动态模糊神经网络对软件质量的预测

宫丽娜，马怀志

0 引言

随着计算机技术的发展，软件质量在软件工业中变得越来越重要。软件质量是软件的天然属性，因此人们需要在软件开发的早期发现软件的质量问题，从而实现对最终软件的质量控制，缩短软件开发周期，减少软件开发和维护成本。软件质量预测建模技术是软件质量评价中的关键技术，通过软件质量预测模型建立软件的内部属性和软件质量之间的非线性关系。

目前国内外在软件质量预测模型领域已有了一定的研究成果。主要有传统的软件质量预测模型和基于神经网络的软件质量预测模型。在传统的软件质量预测模型方面，主要有基于软件的规模和复杂度为度量来预测软件的缺陷数[1],采用了回归方法。此外也有基于测试数据的软件质量预测模型[2]。美国Florida Atlantic University的Khoshgoftaar教授在该领域也做了大量卓有成效的研究工作。Khoshgoftaar和Seliya提出了基于回归树( Regression Tree) 模型对软件各模块中的错误数进行预测的方法[3]，同时Khoshgoftaar 等提出了一种软件质量预测的建模技术，结合了模糊聚类( Fuzzy Clustering)和软件质量预测的模块级别模型( Module-Order Model)[4]。我国的蔡开元教授首先将模糊方法引入软件质量及可靠性领域，提出了模糊软件可靠性的确认模型[5][6]。但是这些方法均有一定的局限性，所基于的模型也比较粗糙，不能比较好地描述软件内部的缺陷和软件所表现出的失效之间的非线性关系。

1 人工神经网络的状况

人工神经网络于 1992年开始应用于软件质量预测模型，取得了比较好的效果。Karunanithi第一次在软件质量预测模型中采用人工神经网络方法，基于一个实际项目的错误数据集合，并采用3个不同的神经网络估计模型来估计累计错误数，通过比较得出比统计模型更好的结果[7]。Nidhi Gupta和Manu Pratap Singh 采用执行时间为B P 神经网络的输入来预测软件可能发生的错误数[8]。Liang Tian和Afzel Noore采用遗传算法来选择最优的神经网络输入层和隐含层神经元个数[9,10]。2001年，Khoshgoftaar介绍了基于高可信系统工程的模糊非线性回归技术，并采用模糊非线性回归技术跟模糊逻辑及神经网络技术结合来预测软件的质量，通过实验产生了更好的实验结果[11]。2002年，Donald E.Neumann 将主成分分析和神经网络技术相结合建立了一个PCA —A N N网络的软件质量预测模型，并通过该模型对软件中的错误进行预测[12]。

综上所述，软件质量预测模型主要是基于软件错误测试报告和软件质量度量，主要应用了统计学和神经网络方法，但目前还没有一个模型被证明是既简单而又广泛通用的。所以针对软件质量预测过程中难以建立精确数学模型的特点，本文将广义动态模糊神经网络应用于软件质量预测模型中，以提高学习效率和精确度。

2 基于广义动态模糊神经网络的软件质量预测模型

2.1 模型自变量

软件质量预测的目的是在软件开发的早期根据与软件质量有关的数据，通过分析计算得到软件质量的预测值，从而对软件系统有个宏观的认识。为了达到这个目的，本文的软件质量预测模型是建立在以软件质量度量为基础上的。

模型的自变量为C&K度量指标表征的面向对象软件的内部属性的 6个度量元，模型的因变量为软件的可靠性[13]-[17]。C&K度量方法是基于继承树的一套面向对象的度量方法，具体的六个度量指标如下：

（1）类的加权方法数 WMC(Weighted Methods per Class )：即为类中方法数的总和；

（2）继承树的深度DIT(Depth of Inheritance Tree)：即为类在继承树的最大深度；

（3）子类的数目NOC(Number of Children)：即为继承树中一个类的直接子类数目；

（4）对象类之间的耦合CBO（Coupling Between Object Class）：即为该类与其他类有耦合关系的数目；

（5）响应集合RFC（Response For a Class）：即为类内部及类之间的通信；

（6）方法内聚缺乏度LCOM(Lack of Cohesion in Methods).

2.2 广义动态模糊神经网络的软件质量预测模型的结构

广义动态模糊神经网络的质量预测模型主要有 4层组成[18]，其具体结构，如图1所示：

图1 广义动态模糊神经网络的软件质量预测模型结构图

第一层为输入层，由C&K度量指标的6个度量元作为输入变量，每个节点对应于输入向量x的第i个分量xi。

第二层为隶属函数层，每个节点代表一个模糊语言变量值，并且每个输入变量 xi有 u个隶属函数Aij(i=1,2…,6;j=1,2…,u)，这些隶属函数为高斯函数，具有表示为公式（1）：

其中，μij是xi的第j个隶属函数，cij和分别为xi的第j个高斯函数的中心和宽度。

第三层为 T-范数层，该层的每个节点代表了一个 RBF单元，模糊规则等同一个RBF节点数。该层用于计算每个触发权的 T-范数算子是乘法，该层第j个规则 Rj的输出是公式（2）：

第四层为输出层，该层的每个节点代表一个输入信号加权和的输出变量，如公式（3）：

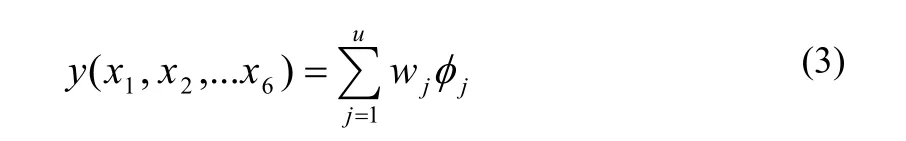
其中，y是一个输出变量的值，即为软件的可靠性，wj是第j个的连接权。该层执行模糊化的功能，同时考虑了所有输出语言值的隶属函数的影响。

通过以上构造的模糊神经网络GD-FNN具有以下特点：

(1)每条模糊规则的T-范数由式（2）来表示，它可以看做是对角化的马氏距离，如公式（4）：

其中，

由此可知，这个模型的接收域是超椭球体而不是 RBF单元中的超球体。

(2)不同的输入变量xi有不同的隶属函数数目也就是说，某个输入变量的隶属函数Aij(j=1,2,…,u)可能会有重复。

2.3 学习算法

广义动态模糊神经网络是基于椭圆基函数，以模糊ε-完备性作为高斯函数宽度的确定准则，避免了初始化过程中选择的随机性，通过对模糊规则和输入变量的重要性的评价使得每个输入变量和模糊规则可以根据误差较少率来修正。该算法能够使参数的调整和结构的辨识同时进行，加快了学习速度。算法的流程图，如图2所示：

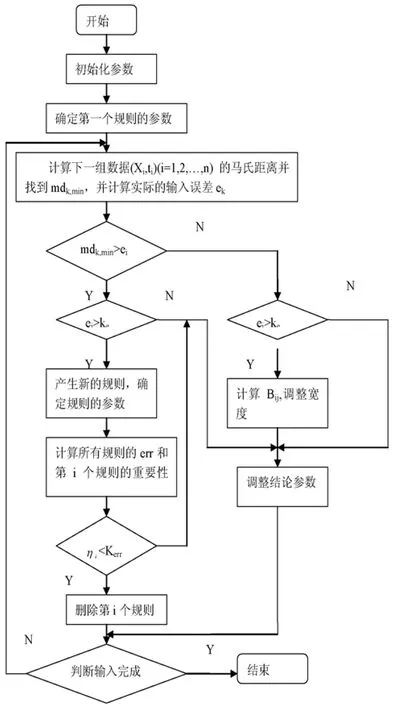
图2 GD-FNN的学习算法流程图

具体的步骤如下：

(1)初始化参数：εmin，εmax，emin，emax，Kmf，ks，kerr；

(2)根据第一组数据产生第一个规则，并确定第一个规则的参数；

(3)计算下一组数据(Xi,ti)(i=1,2,…,n) 的马氏距离并找到mdk,min，并计算实际的输入误差ek

(4)比较 mdk,min和 ei，如果 mdk,min＞ei，则转到（5），否则转到（7）

(5)比较ei和ke，如果ei＞ke，则产生一条新的规则，确定最新产生规则的参数，并计算所有规则的err和第i个规则的重要性jη,否则调整结论参数，转到第(8)；

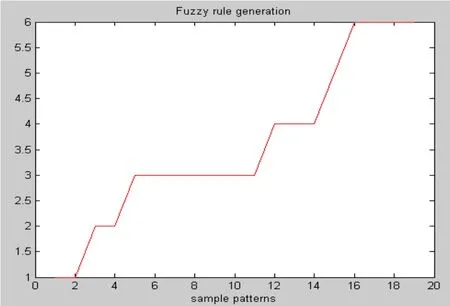
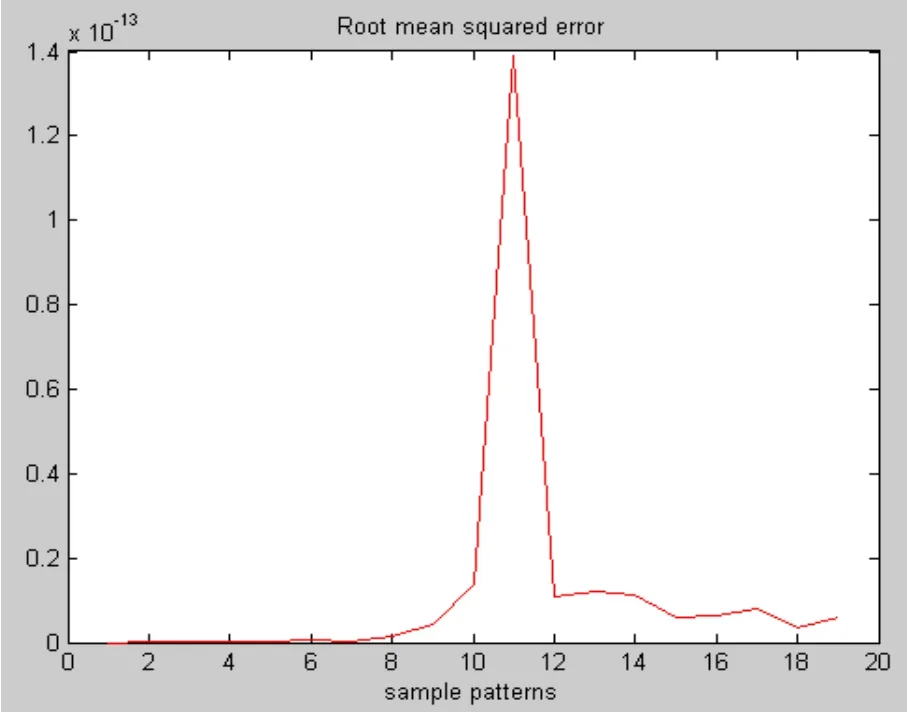
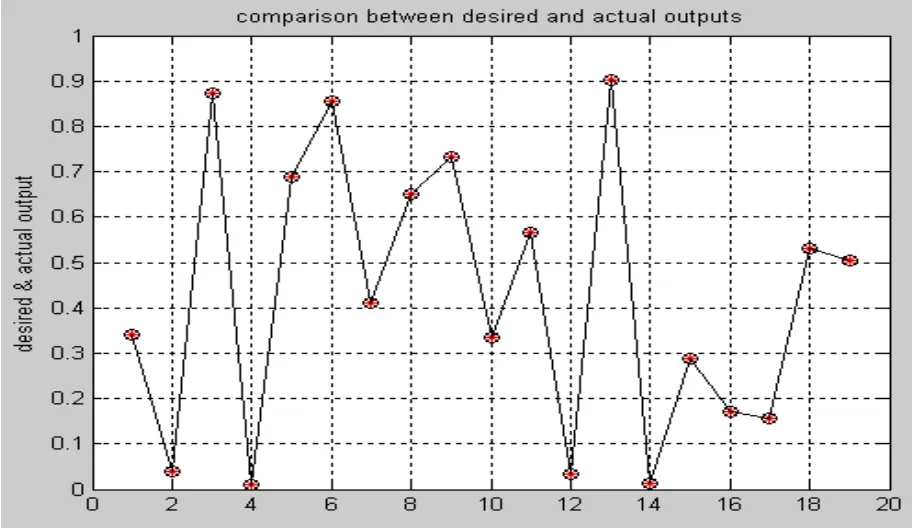
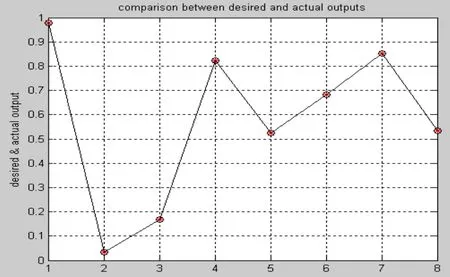
(6)比较Kerr和jη，如果jη

(7) 比较 ei和 ke，如果 ei＞ke，则计算 Bij，调整宽度，调整结论参数，否则，调整结论参数；

(8)判断样本数据是否输入完，完成则结束，否则转到第(3)。

3 仿真实验

本实验选用的软件质量神经网络预测模型是广义动态模糊神经网络，以C&K度量方法的6个度量元：CBO、DIT、NOC、RFC、 WMC、 LCOM作为模型的输入，以可靠性质量属性作为模型的输出。用matlab编程实现，先用19个数据对广义动态模糊神经网络进行训练，然后用8个数据进行验证。在广义动态模糊神经网络中初始化参数为：εm in =0.5；εmax=0.9；emin=0.03；emax=0.5；Kmf=0.5；Ks=0.9；Kerr=0.005。仿真结果，如图3-7所示：

图3 模糊规则产生图

图4 训练样本的均方根误差曲线图

图5 训练样本的实际输出和预期输出比较曲线图

图6 验证样本的均方根误差曲线图

图7 验证样本的实际输出和预期输出比较曲线图

由图3可知，采用广义动态模糊神经网络产生的模糊规则数为6，而通过粗糙集属性约简得到的为16个，明显减少。计算可得训练样本的均方差误差为2.6918×10-14，误差很小，基本上与实际输出相重合，由图5可知拟合的程度，并且由图 4均方根误差曲线图可知每个样本数据的误差都很小。

由图6和图7可知，广义动态模糊神经网络在对前19个训练样本进行学习后，对后8个数据辨识预测的结果基本上和实际数据相重合，每个数据的误差达到 10-15，验证样本的均方差误差为8.4565×10-16，辨识结果比较理想，并且广义动态模糊神经网络的训练速度非常快，效率和学习性能很高。因此，将广义模糊神经网络应用到软件质量预测模型中具有一定的实际意义。

4 结论

广义动态模糊神经网络的结构是扩展的径向基函数神经网络，它基于椭圆基函数，以模糊ε-完备性作为高斯函数宽度的确定准则，避免了初始化过程中选择的随机性，通过对模糊规则和输入变量的重要性的评价使得每个输入变量和模糊规则可以根据误差较少率来修正，并且该算法能够使参数的调整和结构的辨识同时进行，加快了学习速度。因此该模型很适合应用于系统建模。基于此，本文将广义模糊神经网络应用到软件质量预测模型中，通过仿真实验表明，该模型能够比较好的反应软件的内部属性和外部属性之间的非线性关系，在学习效率和性能方面具有更突出的优势。

[1]Hatton, L.C.Safety Related Software Development:Standards, Subsets, Testing, Metrics, Legal Issues,McGraw-Hill, 1994

[2]Fenton, N.E, Lawrence S., Glass, R.Science and substance: a challenge to software engineers, IEEE Software,1994, pp.86-95

[3]Khoshgoftaar, T.M.Seliya, N.Tree-based software quality estimation models for fault prediction, Proceeding of the 8th IEEE Symposium on Software Metrics, 4-7 June 2002, pp.203-214

[4]Khoshgoftaar, T.M., Liu, Y., et al.Multiobjective module-order model for software quality enhancement, IEEE Transactions on Evolutionary Computation, 2004.Vol8,N0.6,pp.593-608

[5]蔡开元，软件可靠性工程基础，[M]清华人学出版社，1995

[6]蔡开元，一个模糊软件可靠性确认模型, []航空学报，1993 年11期，95-98页

[7]Karunanithi, N.Whitley, D.Malaiya.Y.K.Using neural networks in reliability prediction.IEEE Software,1992,9(4): 53-59

[8]Nidhi Gupta, Manu Pratap Singh.Estimation of software reliability with execution time model using the pattern mapping technique of artificial neural network.Computer and Operations research, 2005,32(1):187-199

[9]Liang Tian, Afzel .Noore.Evolutionary neural modeling for software cumulative failure time prediction.Reliability Engineering and System Safety, 2005,87(1):45-51

[10]Liang Tian, Afzel Noore.On-line prediction of software reliability using an evolutionary connectionist model.Journal of Systems and Software, 2005,77(2):173-180

[11]Zhiwei,T.M.Khoshgoftaar.Software quality prediction for high-assurance network telecommunications systems.The Computer Journal,2001,44(6):557-568.

[12]Donal E.Neumann.An Enhanced Neural Network Technique for Software Risk Analysis.IEEE Transaction on Software Engineering,2002,28(9):904-912.