虚拟样机技术在气垫船推进系统特性研究中的应用

张洪田，耿瑞光，孙远涛

(1.哈尔滨工程大学动力与能源工程学院，黑龙江 哈尔滨 150001;2.黑龙江工程学院，黑龙江 哈尔滨 150050)

0 引言

气垫船作为发展迅速的一种特种船舶，有推进系统部件组成复杂、船体刚度较小等结构特点，其推进系统动力学特性同时受船体刚性运动及弹性变形影响［1］。由于船体－轴系耦合问题的复杂性，传统的船舶轴系计算大都建立在刚性船体或船体静态变形的假定上，采用的方法主要为传递矩阵法和有限元法［2－6］。

由于传统计算方法对气垫船推进系统研究的局限性，因此，涉及气垫船推进系统的研究成果还较少。虚拟样机技术是以多体动力学理论为基础、随着现代计算机技术发展起来的研究复杂机械系统的有力工具，常见于航空、航天、汽车等典型多体系统领域［7－9］。鉴于此，本文针对气垫船的结构特点，将虚拟样机技术引入气垫船推进系统的特性研究中。

与典型链式结构的传统船舶轴系相比，气垫船推进系统与船体需要作为一个受外界环境激励影响的整体系统来考虑。

1 多体动力学基本方程

1.1 系统坐标系

高速系统中柔性体的变形对系统整体动力学行为产生很大的影响，针对气垫船推进轴系高速及船体轻质等特点，采用混合坐标来描述气垫船柔性体位形［10］，见图1所示。其中，O为惯性坐标系;o为动坐标系;P为弹性坐标系。

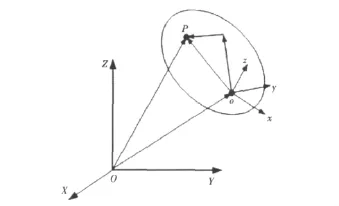
图1 柔性体的坐标系Fig.1 Coordinate system of flexible body

1.2 系统能量表示

1)系统动能

考虑柔性体节点P变形前后的位置、方向和模态，柔性体的动能可表示为:

式中:mp和IP分别为节点P的节点质量和节点惯性张量;vp为节点速度;ωGBp=Bpψ˙为动坐标相对于惯性坐标系的角速度在局部坐标系中的斜方阵表示。

2)系统势能

势能分为重力势能和弹性势能，可用下列二项式表示:

在弹性势能中，K为对应于模态坐标q的结构部件的广义刚度矩阵;ξ为广义坐标;Wg为重力势能。

3)多柔体动力学方程

柔性体的运动方程可由拉格朗日方程导出

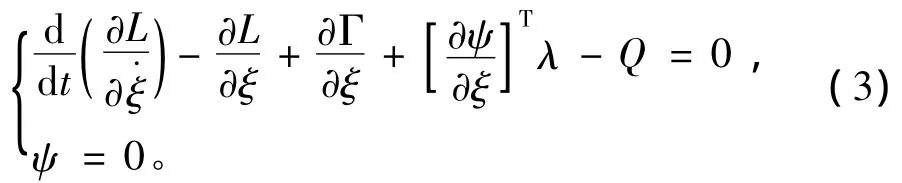
式中:ψ为约束方程;λ为对应于约束方程的拉氏乘子;Q为投影到ξ上的广义力;L为拉格朗日项，定义为L=T－W，T和W分别表示动能和势能;Γ为能量损耗函数。

将求得的T，W，Γ代入式(3)，得到最终的运动微分方程为:

2 气垫船推进系统建模研究

2.1 气垫船推进系统虚拟样机分析流程

气垫船推进系统虚拟样机分析流程如图2所示。

图2 船体－推进轴系虚拟样机分析流程Fig.2 General flow to analyze ship hull-shafting system

2.2 船体建模

为考虑气垫船推进系统受船体弹性变形及刚性运动的影响，需对船体进行虚拟样机建模。柔性船体虚拟样机建模的方法可分为全船有限元建模和空心矩形截面梁建模。

按照Timoshenko梁理论建立的柔性连接梁如图3所示。

图3中，s1，s2和s3为沿梁J标记点坐标轴的作用力;s4，s5和s6为绕J标记点坐标轴的力矩;s7，s8和s9为沿梁I标记点坐标轴的作用力;s10，s11和s12为绕I标记点坐标轴的力矩。

柔性梁按照式(5)计算作用在柔性梁两端的作用力。

图3 柔性梁Fig.3 Flexible beam

式中:Fx，Fy和Fz分别为沿J标记点坐标轴的作用力;Tx，Ty和Tz分别为绕J标记点坐标轴的力矩;x，y和z分别为I标记点相对于J标记点的x向、y向和z向位移;a，b和c分别为I标记点相对于J标记点绕 x轴、y轴和z轴的相对转角;vx，vy和vz分别为x，y和z的时间导数;ωx，ωy和ωz为I标记点相对于J标记点的角速度。柔性梁阻尼阵中的元素Cij可由刚度矩阵中的元素kij与阻尼比R的乘积得到，即Cij=kijR。

分别对柔性梁建模的矩形截面船体和有限元建模的矩形截面船体进行动静刚度比较。图4和图5分别为静态刚度和动态刚度比较。

由图4和图5可以看出，柔性梁船体模型和有限元船体模型在动静载荷的作用下，变形特性是很接近的。同有限元建模相比，柔性梁可以大大减少模型中的自由度数量。因此，基于弹性梁模型建立的船体模型，适用于在概念阶段了解系统的总体性能。在设计初期，可以采用结构简单的弹性梁模型，以减少计算工作量。

2.3 推进轴系建模

推进轴系结构相对简单，可采取有限元方式建模。为处理轴承支承约束单元及柔性体部件和刚体部件的连接以及定义载荷、约束等关系，采用定义有限元模型刚性区域方法并引入主、从节点。其中，轴系部件两端连接弹性联轴器的中心处及轴承支承中心处定义主节点，轴两端及轴承支承处的轴外圆节点定义为从节点，主、从节点通过刚性区域连接。其他部件可通过主节点与柔性体部件相连，外部载荷也可通过主节点均匀加载到柔性体部件上。图6为使用六面体单元SOLID95划分，定义主、从节点及刚性区域的轴系有限元模型。

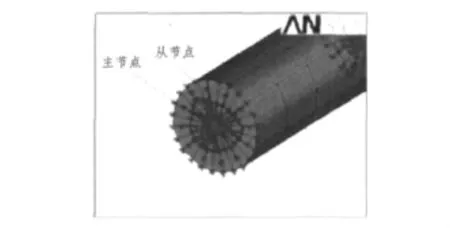
图6 轴有限元模型Fig.6 FEM model of shaft

3 船体－轴系耦合动力学模型

根据气垫船船体－推进轴系耦合运动的结构特点，通过在虚拟样机仿真环境中建立船体运动的状态变量输出和轴系支承运动驱动的状态变量调用，得到船体－轴系耦合动力学模型。

建立系统状态变量的具体步骤为:在船体相对轴系支承处建立船体垂向位移测量监测，通过运行函数表达式定义状态变量函数，定义的状态变量为:

F(time，…)=.model_1.PART_x_MEA_a。(6)其中:model_1.PART_x_为船体名称;MEA_a为船体a点处建立的垂向位移测量。

调用状态变量函数为VARVAL(id)，其中id为所调用的系统状态变量的编号。

4 应用算例

采用本文提出的虚拟样机技术对某型气垫船进行中拱状态下的推进系统动态支承力的仿真研究。仿真结果如图7所示。

图7 中拱时轴系动态支承力Fig.7 Bearing forces of shafting when base's middle haunch-up deformation

5 结语

气垫船推进系统的动力学计算，需要综合考虑船体运动及变形对轴系的影响。针对气垫船的结构特点，本文提出一种基于虚拟样机技术的气垫船推进系统动力学特性的研究方法，对气垫船船体及推进轴系的建模方法进行了比较研究，确立了气垫船船体－推进系统的耦合运动方法。

应用本文的研究成果，可充分考虑海洋环境导致的船体运动变形对推进系统运动特性的影响，为进一步研究气垫船推进系统动力学提供有效的研究手段。

［1］Б.A.柯雷扎耶夫.水翼艇气垫船设计手册［M］.北京:国防工业出版社，1985.

［2］SANKAR S.On the torsional vibration of branched systems using extended transfer matrix method［J］.Journal of Mechanical Design，1979，101(4):546 －553.

［3］WAKABAYASHI K， etal.Analysisofvibrationsof reciprocatingengine shaftings by the transfermatrix method:analysis of forced vibration of a crankshaft［J］.Bulletin of the Marine Engineering Society in Japan，1980，8(1):27－31.

［4］NELSON H D，Mc VAUGH J M.The dynamics of rotorbearing systems using finite elements［J］.ASME Journal of Engineering，for Industy，Transaction，1976，98(2):593 －600.

［5］姜雪洁，耿厚才.船舶推进轴系的动态模型［J］.振动与冲击，2005，24(2):21 －23.JIANG Xue-jie，GENG Hou-cai.Dynamic model of marine shafting system［J］.Journal of Vibration and Shock，2005，24(2):21－23.

［6］魏海军，王宏志，满一新.关于船舶轴系校中计算中的弯矩影响问题的探讨［J］.船舶力学，1999，3(2):44 －48.WEI Hai-jun，WANG Hong-zhi，MAN Yi-xin.The problem on moment influence number of the shaft system alignment of ships［J］.Journal of Ship Mechanics，1999，3(2):44 －48.

［7］邸彦强，李伯虎，柴旭东，等.多学科虚拟样机系统建模与仿真平台及其关键技术研究［J］.计算机集成制造系统，2005，11(7):901 －908.DI Yan-qiang，LI Bo-hu，CHAI Xu-dong.Research on collaborative modeling＆ simulation platform for multidisciplinary virtual prototype and its key technology［J］.Computer Integrated Manufacturing System，2005，11(7):901－908.

［8］王钢林，武哲.基于虚拟样机的飞机总体设计环境的体系研究［J］.航空学报，2005，26(2):162 －166.WANG Gang-lin，WU Zhe.System frame research on aircraftconceptualdesign platform based on virtual prototyping［J］.Acta Aeron Et Astronautica Sinica，2005，26(2):162－166.

［9］钱德猛，赵韩，魏映.汽车振动系统的虚拟样机仿真及试验研究［J］.现代制造工程，2006，(1):74－77.QIAN De-meng，ZHAO Han，WEI Ying.The research on simulation of virtual prototype and experinment to the libration system of automobile［J］.Modern Manufacturing Engineering，2006，(1):74 －77.

［10］MEIROVITCH L.A new method ofsolution ofthe eigenvalue problem for gyroscopic systems［R］.AIAA J.，1974，14(2):453 －465.