基于颗粒轨迹分析的分级机切割粒径计算
岳大鑫,刁 雄,李双跃,黄 鹏
(西南科技大学制造科学与工程学院,四川 绵阳 621010)
研究开发
基于颗粒轨迹分析的分级机切割粒径计算
岳大鑫,刁 雄,李双跃,黄 鹏
(西南科技大学制造科学与工程学院,四川 绵阳 621010)
为研究超细分级机的切割粒径,采用计算流体力学技术对分级机气固两相流进行了数值模拟。计算中气相采用RNGk-ε湍流模型,颗粒相采用随机轨道模型。通过分析颗粒轨迹与切割粒径的关系,揭示了颗粒在分级机内运动的物理机制;通过分析切割粒径随转子转速、风量、喂料浓度和物料密度的变化规律,阐述了各参数对切割粒径的影响。结果表明:切割粒径的理论推算中,忽略叶片厚度的影响将导致计算值偏小;低转速(450 r/m in,600 r/m in)时,受局部涡流的影响,切割粒径模拟值与理论计算值相差较大,最大误差为13.58%;与风量相比,转速对切割粒径的影响更为显著。模拟结果与理论计算值吻合较好,为求取分级机的切割粒径提供了一种新方法。
超细分级机;切割粒径;颗粒轨迹;数值模拟
超细分级机是超细粉体制备过程中的重要设备,其性能的好坏关系到产品的质量和产量,为此,国内外较多学者对其做了相应的研究[1-6]。随着科技的进步和工业的发展,生产、实验中不仅要求分级机有较高的分级效率和分级精度,而且要有较小的切割粒径。陆厚根[7]以离心逆流式气流分级机为研究对象,推导了切割粒径计算式,分析了风量、叶片参数对切割粒径的影响,理论计算值与试验值基本一致;金镛国等[8]通过理论推导研究了操作条件对切割粒径的影响,并提出了新的切割粒径求解方法及适用范围;Xu等[9]模拟了转子叶片间的速度和颗粒轨迹,但并未提出颗粒轨迹与切割粒径之间的关系;杜妍辰等[10]引入一个单颗粒动力学模型,分析了转速、风量、叶片间距及倾角对分级机切割粒径的影响,但未给出切割粒径与这些参数之间的具体关系。以上研究对分析分级机切割粒径起到了一定的指导作用,但由于实验设备和测试手段的限制,研究进展相对缓慢。随着计算流体力学(CFD)的发展,采用数值模拟的方法对分级机进行研究受到了工程技术人员的青睐,但关于分级机切割粒径的数值研究还鲜有报道,而切割粒径是评价分级机性能的重要指标。因此,本文作者采用CFD技术对分级机切割粒径进行研究,并对其影响参数进行分析,为分级机的参数控制奠定基础。
1 切割粒径的理论计算
在分级室内径向方向上,颗粒主要受到剩余离心力Fu和气体曳力Fr的作用,在这两个力作用下,颗粒完成分级,如式(1)、式(2)[11]。

当Fu=Fr时,颗粒在径向方向上处于平衡状态,即一半可能随气流被带出作为产品,一半可能作为粗粉被收集,该颗粒的粒径就是切割粒径d50,如式(3)、式(4)。
不考虑转子叶片厚度的影响

考虑转子叶片厚度的影响

2 物理模型与数值计算
2.1 物理模型与网格划分
分级机叶片数量为36片,厚5 mm,均匀分布在外径为400 mm的圆周上。对超细分级机的模型进行简化和划分网格,由于模型不规则,采用六面体和四面体网格相结合对模型进行分块划分网格,并对转子区域进行网格的加密。经过网格无关性验证,当网格超过83×104时,进出口压差已经变化不明显,继续增加网格数量对流场影响较小,同时考虑计算的经济性,最终确定网格数为837 346,分级机简化结构和网格划分如图1所示。
2.2 数学模型
2.2.1 基本控制方程
分级机内压力低,气体常温流动且速度较低,可视为不可压缩黏性流体,其时均方程组如式(5)、式(6)。
连续性方程

动量守恒方程

式中,为雷诺应力,是湍动对时均流动产生的影响。
2.2.2 RNG k-ε湍流模型
RNGk-ε湍流模型考虑了平均流动中的旋转和旋流流动情况,可以更好地处理高应变率和流线弯曲程度较大的流动[12]。其湍动能与耗散率的输运方程如式(7)、式(8)。
湍动能k

湍动耗散率ε

2.2.3 颗粒运动方程
在拉格朗日坐标系下,采用随机轨道模型计算颗粒运动轨道,颗粒的运动微分方程如式(9)、式(10)。
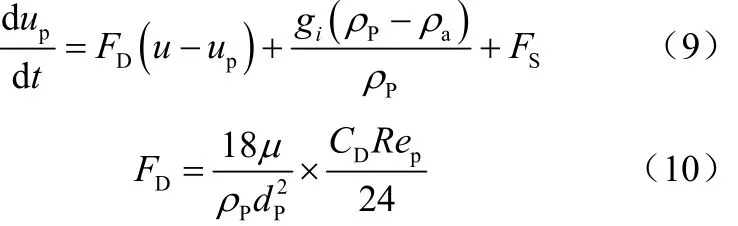
式中,Rep=(ρadp|up-u|)/μ,CD=a1+a2/Rep+a3/Rep,式中a1、a2、a3为常数[13]。
2.3 边界条件
(1)入口边界条件 气相采用速度入口;颗粒相采用面喷射源,颗粒均匀的分布在入口截面上,且速度与入口气速相同。
(2)出口边界条件 气相按充分发展管流条件处理;颗粒相设置为逃逸,下锥体底部设为颗粒捕捉。
(3)壁面处 气相采用无滑移边界条件,并采用标准壁面函数法处理,颗粒相与壁面碰撞恢复系数取0.9。
2.4 求解方法
采用有限体积法进行流体控制方程的离散求解,压力-速度耦合问题采用经典的SIMPLE算法求解,压力项选用标准的Standard差分格式,动量、湍动能、湍流耗散率均采用收敛性较好的一阶迎风格式。两相计算时,由于颗粒体积分数较低(远小于 10%),因此只考虑气相对颗粒相的作用,先计算气相,收敛精度达到10―4后,再将颗粒相从入口截面注入,进行两相求解。
3 模拟结果分析
3.1 颗粒轨迹与切割粒径
粉体分级过程中,颗粒轨迹能较为直观地描述颗粒在分级机中运动过程和变化经历,揭示分级机内气、固分级的机理。在分级室内,颗粒主要在离心力和气流曳力的作用下完成分级。对理想分级来说,当颗粒粒径等于切割粒径时,颗粒作为细粉和粗粉被收集的概率均为50%,而粒径小于切割粒径的颗粒应完全进入转子内部成为细粉,大于切割粒径的颗粒不能进入转子内部而被作为粗粉收集。
以重质碳酸钙(密度为2800 kg/m3)为分级物料,分析不同粒径的颗粒在分级机内的运动轨迹。图2为转子转速900 r/m in、风量3000 m3/h、喂料浓度0.75 kg/m3时,不同粒径的颗粒在分级机内的运动轨迹。模拟结果表明,不同粒径的颗粒在分级机内的运动轨迹不同,粒径小于11 μm的颗粒能通过细粉出口成为细粉,而粒径大于12 μm的颗粒均不能进入转子内部,最终作为粗粉被收集。这与理想分级较为相似,为此,本文定义数值模拟中能进入转子内部作为细粉被收集的最大颗粒粒径为切割粒径d50。由此得出,在此操作条件下,模拟得到的分级机切割粒径在11~12 μm之间,这与按照式(1)计算的10.38 μm和按式(2)计算的11.41 μm较为接近。同理,对转子转速1800 r/min、风量3900 m3/h、喂料浓度1.25 kg/m3时不同粒径的颗粒在分级机内的运动轨迹进行了分析,数值模拟得出的切割粒径在6~7 μm之间,这与按照式(1)计算的5.92 μm和按式(2)计算的6.50 μm吻合较好。说明采用数值模拟的方法能够有效地预测分级机的切割粒径,为切割粒径的求取提供了一种新方法。
3.2 转速的影响
表1反应了物料密度ρ为2800 kg/m3、喂料浓度c为0.75 kg/m3时,切割粒径随着转子转速的变化情况。由表1可知,随着转速的增加,分级机切割粒径显著减小。随着转速的增加,分级室内的分级力场强度相应增加,相同粒径的颗粒所受离心力增加,使得更小的颗粒也能向边壁运动,与壁面碰撞,最终作为粗粉被收集。只有更细的颗粒才能通过转子叶片间隙作为细粉被收集,因此,切割粒径下降。对比不考虑叶片厚度以及考虑叶片厚度的理论计算值和数值模拟得到的结果可知,模拟值与考虑叶片厚度的理论计算值更为接近,而不考虑叶片厚度的理论计算值相对偏小。这主要是因为不考虑叶片厚度,使得气体过流面积增加,在相同体积风量下,径向速度减小。由曳力公式(2)可知,颗粒受到的曳力降低,气体对颗粒的携带能力下降,只有更细的颗粒能够进入转子内部,切割粒径减小。
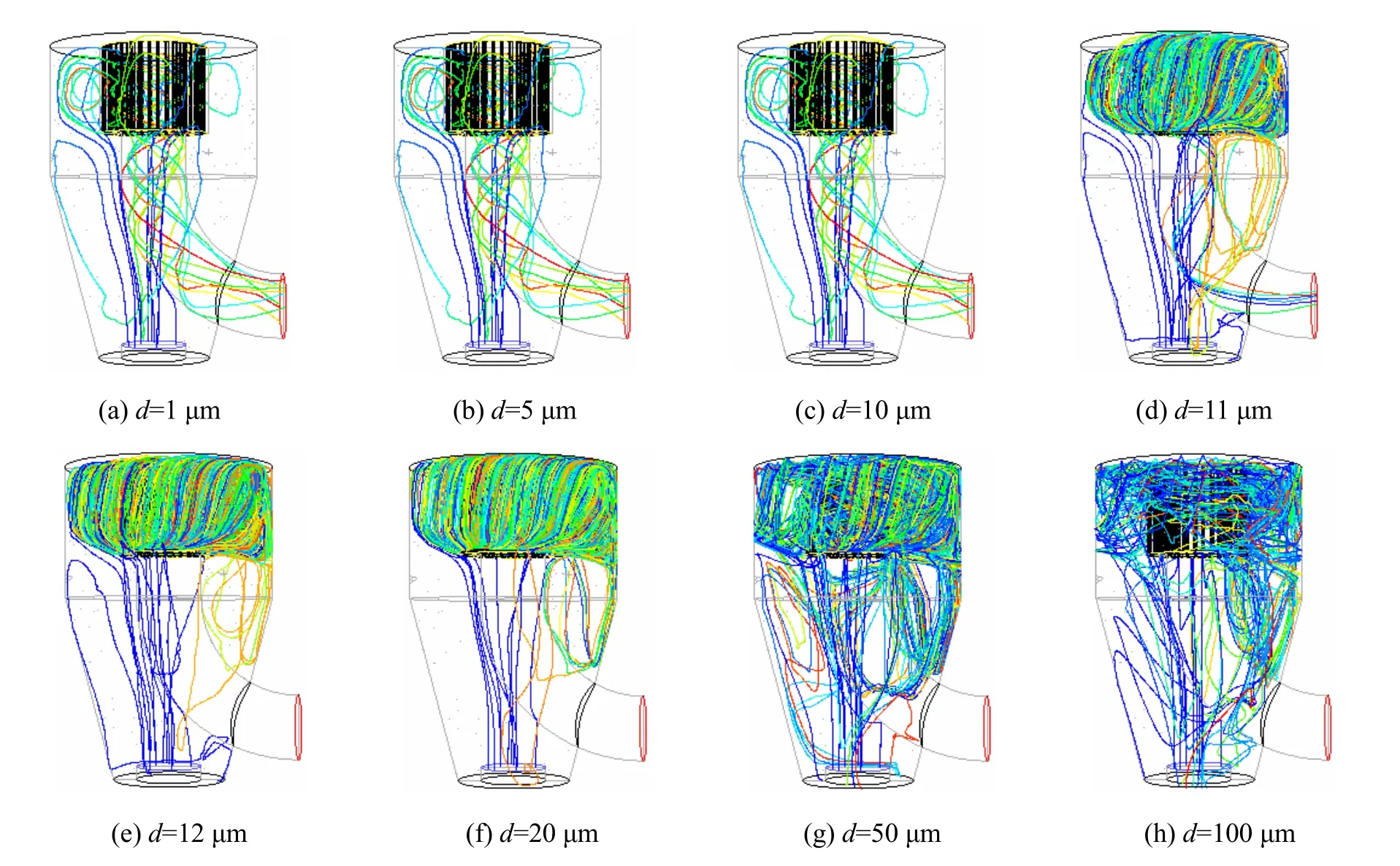
图2 不同粒径颗粒的轨迹线(ρ=2800 kg/m3,n=900 r/min,Q=3000 m3/h,c=0.75 kg/m3)
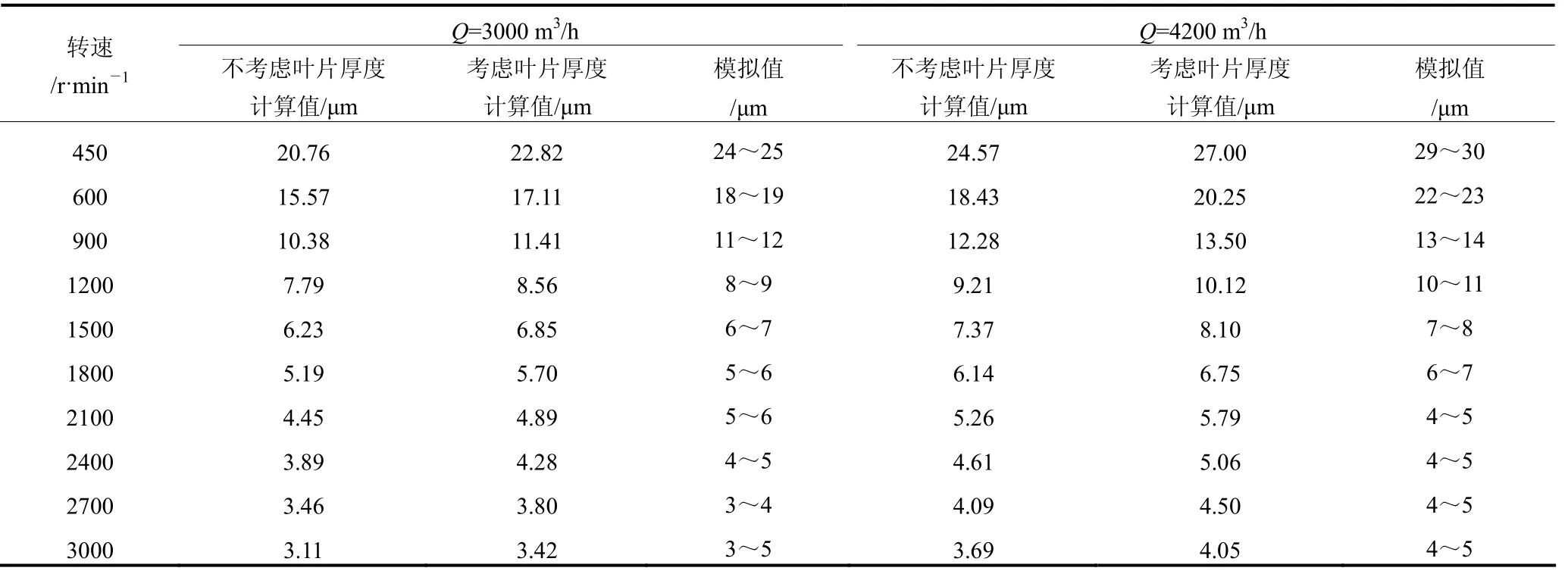
表1 转速对切割粒径的影响
对表1中考虑叶片厚度的理论计算值与模拟值进行误差估计,风量为 3000 m3/h时,在转速为450 r/min处误差最大,为 9.55%,在转速为 1500 r/m in处误差最小,为2.14%;风量为4200 m3/h时,转速为600 r/m in处误差最大,为13.58%,转速为2400 r/min处误差最小,为1.2%。说明在转速较低(450 r/m in,600 r/min)时,模拟得到的切割粒径与理论计算值相差较大。其主要原因为,转速较低时,分级室内易产生局部涡流,涡流会消耗流体的部分能量,同时不利于分级流场的均匀性;而转速的增加有利于提高分级机气流流场的整流性,流场相对稳定,产生较大局部涡流的概率和涡流强度相对较低[14],稳定的流场有利于粉体分级的进行。

表2 风量对切割粒径的影响
3.3 风量的影响
表2描述了物料密度2800 kg/m3、喂料浓度0.75 kg/m3时,切割粒径随着风量的增加而逐渐增大。流过分级机的风量决定了转子叶片外沿气流的径向速度,从而影响颗粒的运动轨迹。随着风量的增加,叶片间气流的径向速度增加,由式(2)可知,颗粒受到的气流曳力增加,气流对颗粒的携带能力增强,在相同离心分级力场中,粒径更大的颗粒能够通过转子叶片间隙进入转子内部并被当做成品收集,切割粒径增大,同时也导致成品中不合格粒径的颗粒增加,影响产品质量。与表1对比可知,风量对切割粒径的影响比转速的影响小,这与理论计算公式的结论是一致的,切割粒径公式中d50正比于风量Q的开方,而反比于转速n。因此,对于切割粒径,风量的影响不如转子转速显著。
对表2中理论计算值(考虑叶片厚度的影响)与模拟结果进行误差估计,转速为900 r/min时,在风量2700 m3/h处误差最大,为8.2%,在风量3900 m3/h处误差最小,为0.08%;转速为1500 r/min时,在风量2400 m3/h处误差最大,为18.3%,在风量4200 m3/h处误差最小,为1.23%。
3.4 喂料浓度的影响
表3分析了两种工况下切割粒径随喂料浓度的变化情况(工况1:物料密度2800 kg/m3,风量3000 m3/h,转速900 r/m in。工况2:物料密度4000 kg/m3,风量3900 m3/h,转速1500 r/min)。由表3可知,随着喂料浓度的提高,数值模拟得到的分级机切割粒径与理论计算值吻合较好,但无明显变化,这与文献[14-16]的试验结果有所不同,文献研究结果表明,随着喂料浓度的增加,单位体积内颗粒的数量增加,颗粒发生碰撞,干涉的概率增加,分散性下降,致使较多细小颗粒相互聚集成为假大颗粒,同时部分小颗粒黏滞在大颗粒上,这些大颗粒最终作为粗粉被收集,而只有更为细小的颗粒能够进入转子内部,切割粒径减小。本文在进行数值模拟的时候并未考虑颗粒的碰撞,团聚作用,同时理论计算公式的推算也是针对分散的单颗粒进行的,因此在结果上与试验结果有所不同,在以后的研究工作中,对于这方面需进一步的深入与细化。
对表3中理论计算值(考虑叶片厚度的影响)与模拟值进行误差估计,工况1最大误差为12.36%,最小误差为3.59%;工况2最大误差为23.43%,最小误差为7.19%。
3.5 物料密度的影响
如表4所示,随着物料密度的增加,切割粒径减小(工况3:风量3000 m3/h,转速900 r/min,喂料浓度0.75 kg/m3。工况4:风量3900 m3/h,转速1500 r/m in,喂料浓度1.25 kg/m3)。密度的增加使得相同粒径颗粒的质量增加,在分级力场中颗粒受到的离心力增大,由于风量并未改变,颗粒受到气流运动所产生的曳力不变,因此在离心力和气流曳力的共同作用下,只有粒径更为细小的颗粒能够进入转子内部,切割粒径减小。
对表4中理论计算值(考虑叶片厚度)与模拟值进行误差估计,工况3最大误差为11.76%,最小误差为0.58%;工况4最大误差为15.25%,最小误差为0.29%。
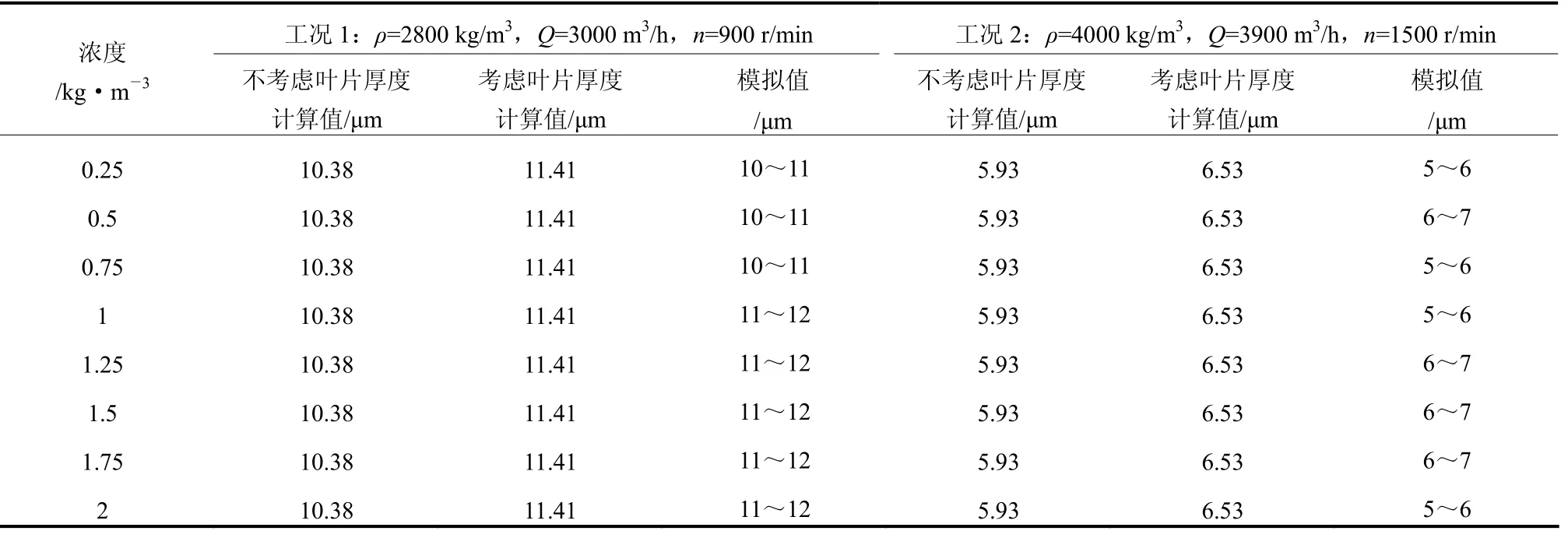
表3 喂料浓度对切割粒径的影响

表4 物料密度对切割粒径的影响
4 结 论
采用RNGk-ε湍流模型和DPM离散相模型对超细分级机气固流场进行了数值模拟,分析了颗粒轨迹与分级机切割粒径两者之间的关系,得到如下结论。
(1)采用数值模拟方法根据颗粒运动轨迹求得的切割粒径与理论计算值吻合较好,为求取分级机切割粒径提供了一种新方法。
(2)切割粒径的模拟值与考虑叶片厚度影响的理论计算值更为吻合。在切割粒径的理论推算中,不能忽略叶片厚度的影响,忽略叶片厚度的影响致使转子叶片间气流速度降低,气流对颗粒的携带能力下降,导致计算的结果比考虑叶片厚度的理论计算值和模拟值小。
(3)在转速较低(文中450 r/min,600 r/m in)时,模拟值与考虑叶片厚度的理论计算值相差较大,最大误差为13.58%,主要是局部涡流使得分级流场不均匀所致。
(4)切割粒径随着转速的增加显著减小,随着风量的增加而变大,随着物料密度的增加而减小。但与风量相比,转速对切割粒径的影响更为显著。
(5)由于文中模拟并未考虑颗粒间的碰撞、干涉和团聚作用,因此在分析喂料浓度对切割粒径的影响时,得出的结论与文献中的试验结果有所差异。减小模拟结果与理论计算值和试验值之间的差距将是以后工作的重点。
符 号 说 明
b——叶片通道宽度,m
CD——曳力系数
c——颗粒浓度,kg/m3
cμ——经验系数
d——颗粒直径,μm
d50——切割粒径,μm
FD(u-up) ——颗粒单位质量曳力,N
Fr——气体曳力,N
Fs——其它相间作用力,N
Fu——颗粒受到的剩余离心力,N
gi——重力加速度分量,m/s2
H——转子高度,m
n——转子转速,r/min
Q——风量,m3/h
R——分级机转子半径,m
Re——气体雷诺数
Rep——颗粒雷诺数
u——气体速度,m/s
up——颗粒速度,m/s
ui,uj——时均速度分量,m/s
ui',uj'——速度脉动量,m/s
Vr——气流径向分速度,m/s
Vu——颗粒切向速度,m/s
xi——坐标轴分量,i=1, 2, 3
z——叶片数量
ρ——物料密度,kg/m3
ρa——气体密度,kg/m3
ρp——颗粒密度,kg/m3
μ——气体动力黏度,0.18×10―4Pa·s
下角标
i——i方向,1,2,3
j——j方向,1,2,3
[1] Ro land N.Fine classification w ith vaned rotors:At the outer edge of the vanes or in the interior vane free area[J].International Journal of Mineral Processing,2004,74(s):137-145.
[2] Rao B V.Analytical expressions for classifier product size distributions[J].Minerals Engineering,2005,18(5):557-560.
[3] Guo L J,Liu J X,Liu S Z,et al. Velocity measurements and flow field characteristic analyses in a turbo air classifier[J].Powder Technology,2007,178(1):10-16.
[4] Feng Y G,Liu J X,Liu S Z.Effects of operating parameters on flow field in a turbo air classifier[J].Minerals Engineering,2008,21(8):598-604.
[5] 刁雄,李双跃,黄鹏,等.SCX超细分级机进料管内气固两相流数值模拟[J].化工进展,2012,31(1):41-46.
[6] Eswaraiah C,Angadi S I,M ishra B K.Mechanism of particle separation and analysis of fish-hook phenomenon in a circulating air classifier[J].Powder Technology,2012,218:57-63.
[7] 陆厚根.离心逆流式气流分级机分级粒径计算与分析[J].同济大学学报,1992,20(3):263-269.
[8] 金镛国,金振中,葛晓陵,等.离心空气分级机中操作条件对分离粒径的影响[J]. 涂料工业,2009,37(9): 54-56.
[9] Xu Ning,Li Guohua,Huang Zhichu.Numerical simulation of particle motion in turbo classifier[J].China Particuology,2005,3(5):275-278.
[10] 杜妍辰,王树林.颗粒在涡轮式分级机分级轮中的运动轨迹[J].化工学报,2005,56(5):823-828.
[11] 刁雄,李双跃,黄鹏,等.超细粉碎分级系统设计与实验研究[J].现代化工,2011,31(4):83-86.
[12] 王福军.计算流体动力学分析——CFD软件原理与应用[M].北京:清华大学出版社,2004:124-125.
[13] Morsi S A,Alexander A J.An investigation of particle trajectories in two-phase flow systems[J].Journal of Fluid Mechanics,1972,55(2):193-208.
[14] 陈海焱,陈文梅,胥海伦.气流分级机操作参数对分级性能的影响[J].四川大学学报:工程科学版,2006,38(3):87-91.
[15] 刘雪东,卓震.超细气流粉碎分级系统产品粒径的确定与控制[J].石油化工高等学校学报,2001,14(1):59-63.
[16] 刘家祥,徐通模,徐德龙.涡流空气分级机内固体浓度对其分级效果的影响[J].西安建筑科技大学学报,2001,33(2): 135-137.
Com putation of classifier cut size based on analysis of particle tracks
YUE Daxin,DIAO Xiong,LI Shuangyue,HUANG Peng
(School of Manufacturing Science and Engineering,Southwest University of Science and Technology,M ianyang 621010,Sichuan,China)
In order to study the cut size of a superfine classifier, computational fluid dynam ics was used to simulate the gas-solid two-phase flow in the classifier. The RNGk-εturbulence model was adopted to describe the gas phase, and the particle stochastic trajectory model was used to describe the solid phase. The physical mechanism of particle movement and the classification process in a superfine classifier was revealed by analyzing the relationship between particle tracks and cut size. By analyzing the change of cut size, the effects of rotational speed, air volume, feeding concentration and material density on cut size were established. The results showed that in the theoretical calculation of cut size, ignoring the effect of blade thickness would lead to overly small calculated value. When rotational speed was low (450 r/m in,600 r/m in), the simulation value and calculated value had a large difference due tor the effect of local turbulence, and the max error was 13.58%. Compared w ith air volume, the effect of rotational speed on cut size was much more significant. The simulation cut size value agreed well w ith theoretical calculation. The results provide a new method of obtaining the cut size of a superfine classifier.
superfine classifier;cut size;particle tracks;numerical simulation
TD 454
A
1000–6613(2012)09–1919–06
2012-03-21;修改稿日期:2012-05-10。
国家科技支撑计划(2011BAA04B04)及西南科技大学研究生创新基金(11ycjj30)项目。
岳大鑫(1956—),男,副教授,从事机械设计与制造方面的教学与研究。E-mail 514027154@qq.com。联系人:刁雄。E-mail diaoxiong1986@163.com。

