三维计算全息显示技术研究概况

张发平

（电子科技大学物理电子学院，四川 成都 610054）

三维计算全息显示技术研究概况

张发平

（电子科技大学物理电子学院，四川 成都 610054）

文章简单介绍了计算全息的原理、发展概况和计算全息的制作方法，分析总结了目前计算全息在三维显示方面所面临的技术瓶颈问题。

计算全息；全息编码；三维显示；发展概况；技术瓶颈

在科技和信息技术飞速发展的今天，三维立体显示技术备受人们亲睐。特别是3D电影和全息投影仪的推广与普及以及对立体电视贫民化的期待，人们在不断地追求着高质量高要求的立体观感需求。然而，真正的立体显示技术仍然是全息显示。全息是一种不同于普通照相的光学技术，利用了光的干涉和衍射原理，制作全息图和再现真三维立体图像，可以给人身临其境的逼真感。全息发展至今已经到了第三个阶段，关于用全息技术再现虚拟大场景也是这个阶段的热门研究方向之一。

1 计算全息的原理和发展简介

20世纪70年代，随着计算机制图和全息技术的高速发展，促使一种很特殊的全息技术——计算全息（CGH）的产生。之所以说计算全息是一种很特殊的全息方法，因为它和之前普通的光学全息有很大的不同，计算全息的输入图片不是实景图片，而是应用计算机软件和数学建模绘制出来的所需要的虚拟的图像场景图片，然后把这种图片做全息编码后输入到空间光调制器显示屏，用干涉光对其照明重现。由于全息图是根据计算机软件任意绘制的，所以从理论上讲可以随心所欲地得到需要的全息图，增强了制作全息图的灵活性。最开始提出计算全息的是柯兹玛和凯里（A.Kozma and DL.Kelly），他们在研究复数空间滤波器时应用数字计算机综合制作了全息图【1】。后来罗曼（A.W.Lohman）引入抽样定理，保证了用离散数学公式描述的复振幅的完整性，并提出迂回相位效应，证明了编码绘制图的正确性。1967年巴里斯（D.P.Paris）把快速傅里叶变换算法应用到快速傅里叶变换计算全息图中，并且与罗曼一起完成了几个用光学方法很难实现的空间滤波，让计算全息得到了长足发展。1969年赖塞姆等人又提出相息图，1974李威汉提出计算全息干涉图的制作技术。计算全息的最常见的应用范围有：二维和三维物体像的显示、在光学信息处理中用计算全息制作各种空间滤波器、产生特定波面、全息干涉计量、激光扫描器和数据存贮等。

2 计算全息制作方法简介

计算全息制作主要包括以下三个步骤：场景的绘制、抽样、编码、计算和再现。傅里叶变换是一种经典的数学变换，在光学中，光经过傅里叶透镜的结果就相当于做一次傅里叶变换，因此采用菲涅耳快速傅里叶变换的方式制作全息图是最常见的方法。

2.1 抽样并计算输入光波

计算全息的物体不是实际物体，可以是电脑绘制的虚拟场景或者图像信息。常使用Matlab编程绘制简单图形进行数值计算，对物光取样时，需满足Whittaker-Shannon采样定律。绘制“128 128”像素大小的字母“F”，设定好“128 128”大小的零矩阵O，用Imread()函数读入到零矩阵O中。

由于需要做离散快速傅里叶变换，处理结果动态变化范围较大，会影响最终的全息图效果。因此需要对读入的光波信息附加一个随机相位，即用值在0到1之间与O数组等大的随机函数矩阵 r = r and(J,K) 乘以光波函数，结果为：O(m,n)=Amnexp(j2r )，此步骤相当于在做光学全息拍照时加上一块毛玻璃，使物光均匀散射照在干板底片上。

在使用离散傅里叶变换（DFT）时，在 ，y方向上会发生J/ 2，K/ 2的相移，需采用fftshift（）相移函数将低频部分调整到中心。

2.2 编码

输入的光波函数是复函数，设Omn=Pmn+Qmni，则其幅值和相位分别为：

编码是将物光的复函数变为非负实数在物理介质中记录下来。常见的编码方式有两种：博奇型编码法和罗曼Ⅲ型编码法。

2.2.1 博奇型编码法【2】

博奇型编码是利用物光和参考光干涉叠加编码振幅和相位，用抽样单元上灰度变化来表示非负实数完成编码。设物光为：O(m,n)=Amnexpj(m,n)，干涉光表达式为：R(m,n)=Rexp(j2πβm)。设记录底片透射率是线性相关的，则相干叠加后：

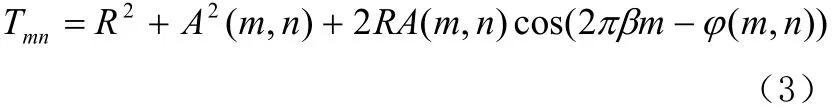
式中，第一，二项是零级干涉项，是直透光部分，第三项是干涉调制项，记录了干涉条纹。可以去掉零级信息，改造函数为：

对上式用Matlab计算，通过空间光调制器调制输出全息编码图。

2.2.2 罗曼Ⅲ型编码法【3】

罗曼编码也称为迂回相位编码，下面以二元计算中最广泛的编码方式罗曼Ⅲ型编码为例作简单介绍。

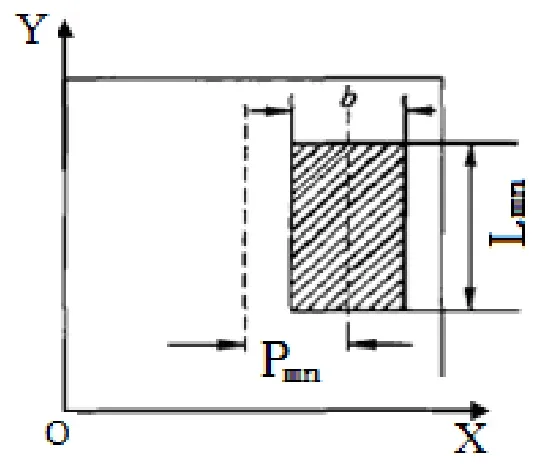
图1

如图1所示，在抽样单元内设定一个矩孔作为透光孔。孔的高度与归一化振幅成正比，比例系数为y，设高为mnL，光波振幅为mnA，mnP为抽样中心到孔中心的间距，与归一化后的相位成正比，比例系数为x，则有：

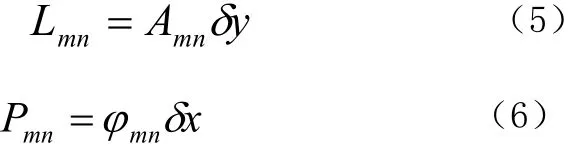
所有取样单元宽度相同，都为b，一般取到倍x。依次确定出矩形孔的位置和大小后，在 Matlab中将其值置零，再翻拍成负片后成为透明孔，这样就完成了对物光的编码。要注意的是当ϕmn大于 时，会造成相邻取样单元重叠，需要将溢出部分移至两端。

2.3 再现

再现方式包括光学再现和计算机仿真再现。以博奇型编码方式获得全息图后，对其用fftshift(fft2())函数实现傅里叶逆变换，模拟再现全息图像。图2为输入图像，图3为利用博奇编码后得到的全息图，图4为模拟再现图【4】。

图2

图3

图4

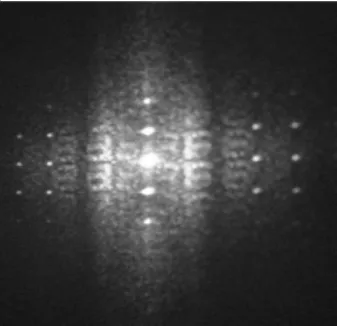
图5

计算全息图也可以利用光学的方法再现。图6是计算全息光学再现的一种光路图，细激光束经过扩束准直起偏后，入射到空间光调制器显示全息图像，在空间光调制器后置一偏振片，调制后的光束通过偏振片再进入傅里叶透镜进行逆傅里叶变换，用CCD接受再现光学图像。由于用到CCD接收光信息，此种方法也可以叫做数字全息，其实在实际中计算全息和数字全息技术总是交叉相关联地使用。图5为采用罗曼Ⅲ型编码光学再现全息图【5】。

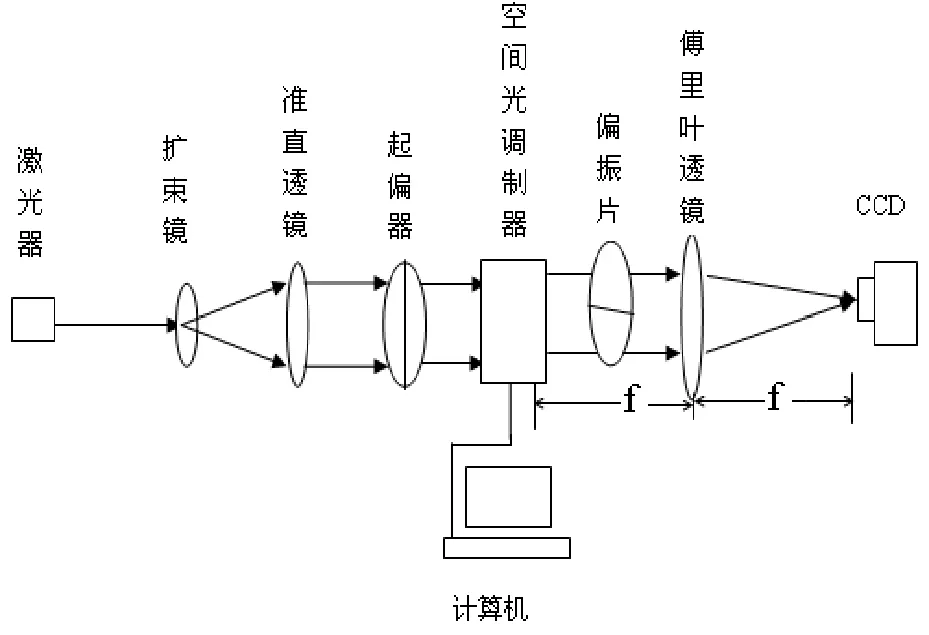
图6

3 计算全息在三维显示方面研究现状

计算全息三维立体显示在军事地图演示，广告展览等方面蕴含着巨大的发展潜力。但是由于现有技术和条件的限制，在合成大场景大视角的计算全息方面还存在诸多的技术瓶颈，下面就计算全息在三维立体显示方面的研究现状和需要解决的问题作一个简述。

3.1 理论模型和算法

理论模型和算法一直是研究计算全息技术的重点与难点，国内外很多研究人员都做了这方面的工作。Haist等【6】基于二维 Gerchberg-Sax-on算法，提出三维Gerchberg-Saxton算法， 通过在全息图中引入发散球面波因子,优化迭代生成能再现空间三维光场的傅里叶计算全息图。Courtial等利用这种方法，在7 mm×7 mm×100 cm的空间内再现出层间距大于 30 cm 的“1”、“2”、“3” 等数字【7】，但由于没有使用大数值孔径的透镜会聚，再现像的尺寸和层间距相当大， 所用的 SLM 较低的填充率和分辨率也造成再现时散斑较多和图像均匀性欠佳。Shimobaba等【8】利用反射型LCD 作为空间光调制器，红、绿、蓝三种颜色的LED 作为参考光源照射LCD，投影出真三维彩色图像，在此基础上,又采用红、绿脉冲激光器以及时分复用的方法重构出了三维彩色像【9】。Makow ski等【10】则利用一种基于GS 算法的多平面迭代菲涅尔卷积算法，生成多平面的位相型计算全息图。但卷积算法决定了三维再现的每一截面的分辨率与SLM的像素大小相同，受限于目前普遍较大的SLM 像素尺寸，局域性也逊于菲涅尔透镜法【11】。Yamaji等【12】用电子束光刻和反应离子刻蚀的方法在玻璃上制作二元位相全息图，获得 8层 16个点组成的分散双螺旋结构。但采用了计算效率较低的直接搜索算法; 每个截面只包含数量极少的点，也难以形成连续变化的复杂结构。我们小组提出的一步全息光刻法【13】，结合位相控制技术【14】，可以快速、方便地曝光感光材料以制备带缺陷的一维、二维和三维光子晶体。葛宝瑧等【15】以博奇编码法制作三维物体的离轴菲涅尔全息图，并通过计算机进行数字再现，得到层间距为5 cm较清晰的再现像。另一类方法是，记录三维物体在非相干光照明下两个正交方向上不同视角的一系列投影像，用这些投影像的频谱信息合成三维物体的波前【16-18】，或将组成三维物体的各点的菲涅尔波带叠加【19-20】，获得三维物体的全息图，这类方法适于记录和再现物体表面形貌，但无法表现被遮挡的结构。

3.2 透镜和记录材料对大幅面计算全息的影响

自从90年代起，美国MIT media实验室致力于大角度，大视场数字合成全息图的研究，并为能克服大视场而引起的图像变形问题提出了新的方法，Michael等人运用一种数字图象变换技术，在拍摄全息图之前对二维图象进行处理，以校正由观察视场较大引起的图象畸变。该实验室制作了首幅大视角全息图，一幅lm×lm的有雪佛来汽车标志的车轮【21】。同时还制作出其他一系列高质量，高象素，无畸变的数字合成全息图，这些标志着运用图象变换技术在实验室研究阶段取得了成功。后来美国Zebra公司制作出了全世界最大的全息图，它是一幅光聚合物干板的，16英尺×4英尺，真彩色，全视差，大视角数字合成全息图【21】。该全息图拍摄了一辆福特公司的概念车，全部图象由计算机生成，每一微元(hoge1)为2mm×2mm，上万个hogel共同显示了一个2英尺×2英尺的“小板”(tile)，由多个tile显示整个图象的各个部分，最终构成一个大幅合成全息图。在合成大幅面动态计算全息图时，往往采用狭缝来分割场景，以获得水平视差图合成动态立体图像。但是相邻狭缝会在相邻亮条纹之间形成重叠暗纹，并且狭缝太细，没有足够光透过，最终影响成像暗淡。后来人们使用平行柱状透镜组来实现场景的分割，虽然解决了图像暗淡的问题，但是由于柱状透镜的像差和像散问题，使得在图像拼接时不能恢复原图。因此改善光路系统，寻找更高分辨率和大尺度记录材料方面对大幅面计算全息的制作是十分必要的。

3.3 三维物体光波场的获取

限制计算全息不能实用化的关键因素，就是如何有效地获取三维物体的光波复振幅光场。主要报道有利用普通体视照相机获得多视角平面图，然后进行适当的数字处理融合出三维信息，但是这种技术计算十分繁琐和费时。还有采用三维数字扫描仪获得三维物体数字化空间分布，然后根据光的传播原理模拟物光的分布，建立三维物体的光场分布，并且根据消隐原理，采用全息分区消隐方法，减少计算量。这种方法能够有效快捷地获得物体的三维光场信息，但是限于较为简单的三维物体。如何能快速有效地获得复杂物体的三维光场信息，需要提出新的获取方法。

3.4 获取大视场全息方法

目前获得大视场全息方法有两种：一是预成像法，二是图像拼接法。预成像法是指先将较大的三维物体用透镜成像后，在用CCD接收干涉图样。虽然这种方法可以有效地扩大视角，但是需要平行光对三维物体照明，而当物体很大时，就不容易实现。况且由于CCD像素限制，扩大了视场，降低了分辨率，影响成像质量。拼接法是将三维物体移动，分各个小部分采集全息图，然后将各个小全息图拼接起来，以扩大视场。这样就可以克服CCD接受面小的缺点，但是增加了图像信息，从而增加了计算量。采用图像拼接法还受限于空间光调制器尺寸和分辨率的影响。因此大尺寸高分辨率 SLM的制作对计算全息来说也是个迫切需要解决的问题。

4 小结

总之，计算全息技术正在逐渐发展之中，很多研究人员在相关方向上都取得了突破性的进展。但是仍然在算法方面，在获得大场景大视角计算全息图方面还存在一些技术或者客观条件限制问题，期待我们进一步研究解决。

[1] 林铁生,徐长远,杨志敏,等.计算全息术的现状和展望[J].中央民族大学学报,1997,6(2).

[2] 康果果,谢敬辉,齐月静,等.用Matlab和LCD实现数字全息图的制作和再现[J].北京理工大学学报,2005,25(6).

[3]刘继芳.现代光学[M].西安:西安电子科技大学出版社,2004(8).

[4][5]黄永峰,孙欣.傅里叶计算全息术及光学再现[J].青岛大学学报(自然科学版),2006,19[1](4).

[6] HAIST T,SCHKLEBER M,TIZIAN I H J. Computer generated holograms from 3D-objects written on twistednematic liquid crystal displays[J]. Opt Com mun,1997,140:299-308.

[7] SINCLAIRG,LEACH J. JORDAN P,et al Interactive application in holographic optical tweezers of a multi-plane Gerchberg-Saxton algorithm for three-dimensional light shaping[J].Opt Express,2004,12(8):1665-1670.

[8] ITOT,SHIMOBABA T,GODOH,et al Holographic reconstruction with a 10 m pixel-pitch reflective liquid crystal display by use of a light-emitting diode reference light[J]. Opt Lett.2002,27(16):1406-1408.

[9] SHIMABABAT,ITOT. A color holographic reconstruction system by time division multiplexing with reference lights of laser[J].Opt Rev,2003,10( 5):339-341.

[10]MAKOWSKIM,SYPEKM,KOLODZIEJCZYK A,et al.Three-plane phase- only computer hologram generated with iterative Fresnel algorithm [J]. Opt Eng,2005,44(12):125805-1-125805-7.

[11]MAKOW SKIM,SYPEKM,KOLODZIEJCZYKA，et al Iterative design of Multi-plane hologram s: experiments and applications [J].Opt Eng,2007,46(4):045802-1- 045802-6.

[12] YAMA JIM， KAWASHIMAH,SUZUKI J,et al. Three-dimensional micromachining inside a transparent material by single pulse fem to second laser through a hologram [J]. ApplPhysLett.2008,93(4):041116-1-041116-3.

[13]LI JT,LIU YK,XIE XS,et al Fabrication of photonic crystals with functional defects by one-step holographic lithography[J].Opt Express,2008,16(17):12899-12904.

[14]XIE XS,LIM,GUO J,et al Phase manipulated multi-beam holographic lithography for tunable optical lattices[J].Opt Express,200715(11): 7032-7037.

[15]葛宝臻,罗文国,吕且妮,等. 数字再现三维物体菲涅耳计算全息的研究[J].光电子 ·激光,2002,13(12): 1289-1292.

The research overview on CGH technology of three-dimensional display

This paper gives a brief introduction to the principle of CGH, study progress and method of making CGH. Analyze technical bottleneck problems in three-dimensional technology of CGH in currently.

the current calculation in3 d holographic display in the face of

Computer-hologram; Holographic code; Three-dimensional display; Development situation; Technical bottleneck

O438

A

1008-1151(2012)06-0051-03

2012-04-21

张发平（1980-），男，四川乐至人，电子科技大学在读硕士研究生，研究方向为信息光学。