修正Kalman滤波在北斗授时中的应用

张向征，乐四海，陶春燕，孔 维

(北京环球信息应用开发中心，北京 100094)

0 引言

北斗卫星导航系统采用主动式双向测距实现二维导航，且三维定位精度约几十米，授时精度约100 ns［1］。北斗系统为了统一时间，需要一种手段将基准时间信号传递给用户以实现时间同步，这就是时间的传递，也叫做授时。北斗单向授时用户利用北斗卫星的出站信号广播2颗卫星的位置、速度和电波传播修正以及中心站至导航卫星的精确上行传播时延值等参数，通过计算机对采集的数据进行统计处理，根据处理结果对本地时钟进行改正，实现北斗时间同步［2］。由于北斗用户单向授时精度要求高，而影响单向授时精度的因素较多，下面通过对北斗单向授时原理进行了分析，结合北斗用户设备单向授时精度，针对卫星广播参数的上行时延值连续波动影响授时精度问题，提出了基于修正Kalman滤波算法能够彻底解决用户单向授时异常问题。

1 单向授时原理

中心站每分钟以一个超帧的形式经卫星向用户发送出站信号，在每一超帧的广播信息中发播授时信息，授时信息包括时刻、闰秒、时差、卫星位置、卫星速度、上行时延和电波传播修正模型参数等。用户接收中心站播发的授时信息，同时用户机的时间间隔计数器以本地钟秒信号1 pps作开门脉冲，以调制解调器检测出的第n帧询问信号的参考时标作关门脉冲测得ΔT'，如图1所示。

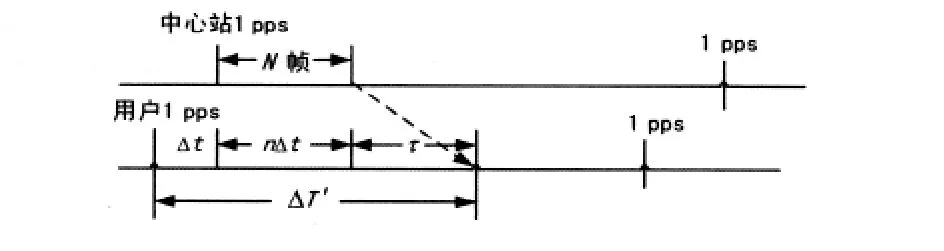
图1 单向授时原理

则用户钟差ΔT与ΔT'的关系为:

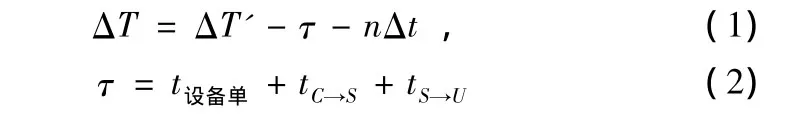
式中，t设备单为指信号在单向传播过程中所经设备的总时延;tC→S为上行时延，即中心站至卫星的距离时延值;tS→U为下行时延，包括卫星至用户的距离时延即真空传播时延tS→U'以及该路径上由对流层和电离层折射产生的传播附加时延t(θ，φ)，计算方法如下:

卫星至用户的真空传播时延为:

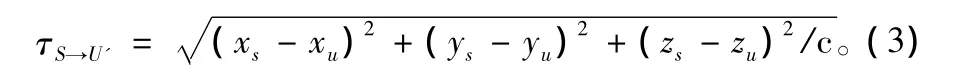
卫星至用户的电波传播附加时延为t(θ，φ)，根据单向授时电波修正的数学模型:

由于 ( xs，ys，zs)与 ( xu，yu，zu)已知，则卫星至用户的真空传播时延τS→U'为真值;ΔT'为定时终端计数器测量时差值(假设为准确值)，nΔt为常数，用户钟差ΔT仅与tC→S和t(θ，φ)有关。而传播附加时延 t(θ，φ) 误差约为 20 ns［3］。

因此，若单向授时用户时间跳数大于100 ns，由式(1)～式(4)可知，用户钟差ΔT仅与tC→S相关。

2 修正卡尔曼滤波算法

根据卡尔曼滤波算法原理可知，当在测量序列中出现野值时，必将影响新息序列的原有性质，导致滤波器估计不准，滤波精度下降。基于卡尔曼滤波器新息序列的特性，这里采用对卡尔曼滤波新息序列进行修正，提高测量野值鲁棒性:在判断存在测量野值的情况下，用一个活化函数加权于新息序列，通过在线修正新息序列，使修正的新息序列能够保持原有的性质，从而达到消除测量野值对滤波器估计结果的不利影响，提高估值的准确性［4，5］。

包含测量野值的离散Kalman滤波模型为:

式中，ρk为测量野值;yk∈Rm。上述离散系统的卡尔曼滤波递推公式为:

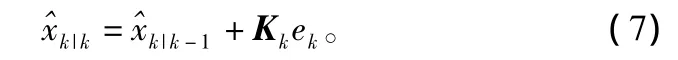
式中，Kk为当前时刻滤波器增益矩阵;ek=yk－为传感器测量值与卡尔曼滤波器输出估计值之差即新息，ek可以看作是yk与的线性组合，容易得到，在滤波结果趋于稳定时，新息序列服从多维正态分布 ek～ N( 0)，其 中=+Rk，Px，k|k－1为状态变量当前时刻估计协方差。

新息序列的统计特性直接反映出测量参数的统计特性，因此可以通过对新息序列的分析判断当前系统测量参数中是否存在野值。由于新息序列为高维向量，直接对其进行分析比较复杂，因此构造新息序列的标量变量为:

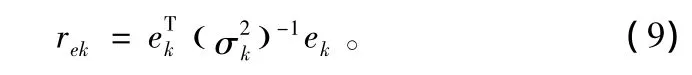
容易得出，变量rek服从自由度为m的分布，即有rek～λ2(m)。rek反映了新息序列的统计特性，而新息序列的统计特性又可以反映出测量值的统计特性［6］。当测量参数中存在野值时，rek特性也随之发生改变。在判断是否存在测量野值后，通过对卡尔曼滤波算法进行修正，提高算法对于测量野值的鲁棒性，减小野值对估计结果的影响。

式中，Φk( rk)为活化函数，用于消除测量参数中野值对于滤波器估计结果影响，通过活化函数对新息序列进行修正，保证新息序列特性不变，消除野值对于滤波器估计值的影响，保证上行时延估值的准确性，算法仿真如图2所示，图2(a)为仿真信号图，图2(b)为加入修正前后卡尔曼滤波算法仿真图。仿真结果表明，针对脉冲野值信号，修正的卡尔曼滤波算法平滑野值，效果明显。

图2 修正卡尔曼滤波效果

3 实例分析

提取2010年4月19日中心站广播星历数据(包含上行时延和附加时延值)和北斗单向定时终端设备的数据分析，验证单向授时精度异常与上行时延值波动较大有关。

由于中心站广播上行时延频度为1次/min，而中心站→卫星→中心站的单向时延测量值τ更新频度为1次/5 s，利用每分钟内多个单向时延测量值，采用线性Kalman滤波算法进行滤波，估计并给出下一整分钟上行时延值的插值，即为该时刻所广播的上行时延值，而当某时刻中心站测量的单向时延测量值τ发生大的跳变时，若仍采用线性Kalman滤波算法估算上行时延值，其值会变化较大而无法使用，如图3(a)所示，直接影响用户单向授时精度。为了解决问题，提出了基于修正的卡尔曼滤波算法估计上行时延值的方法，通过对卡尔曼滤波算法进行修正，提高算法对于测量野值的鲁棒性，减小野值对估计结果的影响，上行时延值经过卡尔曼滤波后结果如图3(b)所示。

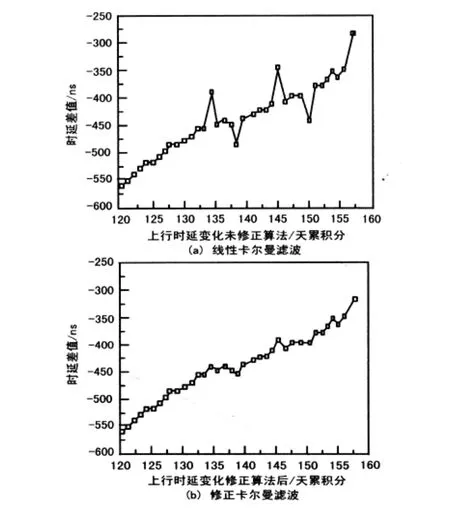
图3 上行时延变化

4 结束语

通过对北斗卫星导航系统广播上行时延值的分析，确定其变化直接影响了用户单向授时精度。采用修正卡尔曼滤波算法估计上行时延值，结果显示，在存在测量野值的情况下，线性Kalman滤波估计出现了较大的偏差，而修正卡尔曼滤波算法保证了较高的估计精度，从而确保了北斗用户单向授时精度。■

［1］张继荣.基于SDH的时间传递方法研究［D］.北京:中国科学院研究生院，2008:12－15.

［2］谭述森.卫星导航定位工程(第2版)［M］.北京:国防工业出版社，2010.

［3］谭述森.广义RDSS全球定位报告系统［M］.北京:国防工业出版社，2011.

［4］张 鹏，黄金泉.基于双重卡尔曼滤波器的发动机故障诊断［J］.航空动力学报，2008(5):10－14.

［5］张 帆，卢 峥.自适应抗野值 Kalman滤波［J］.电机与控制学报，2007，11(2):188 －190.

［6］罗志斌，刘先省，胡振涛，等.基于新息特性抗野值Kalman预测算法［J］.河南大学学报，2006，36(4):79－82.