数学规划在企业管理中的应用探讨:以服装企业为例
成都职业技术学院 左莉
随着全球化经济过程的加快,企业所处的环境越来越变得复杂,现代企业处在一个竞争激烈、瞬息万变的国际市场中。各国企业都在加强技术创新,改革的步伐急剧加速,管理更加科学化、精益化、信息化,强调精密控制的现代系统管理理论尤其是数学规划在企业管理中的地位和作用越来越突出。
数学规划是运筹学的一个分支,是解决多阶段决策过程的最优化问题的一种方法,在企业管理中有着非常重要的作用。数学规划作为系统管理中的重要手段,在现代企业管理中发挥着越来越重要的作用。针对实际问题中某些非线性问题可能有最优解这一特点,数学规划是众多解决方案中求解该类问题最优解的一种有效的方法。许多看似无法精确的企业实际问题,通过用数据规划,建立相关的数学模型,常比非线性估计来得更为精确和有效。
用线性规划法解决问题的过程,首先是提出经济问题,然后建立数学模型,再解决计算方法,最终根据求解结果进行决策。求解线性规划问题的方法有几何解法(图解法)、单纯型法、代数解法。
1 数学规划方法与模型
在现代企业管理中,不同的行业、不同的企业采用适合其自身的数学规划的方法和模型。有几类数学规划方法与模型是在企业管理中运用得最为广泛的,也是最为重要的。
AHP层次分析法是美国管理学家T·L·Saaty经过研究得出的一种系统性的分析方法,在决策、预测、评估等企业管理活动中运用非常广泛,是系统研究最为常用的研究方法,AHP层次分析法是根据所要解决的问题的性质和企业需要达到的总体目标,将非常复杂的问题按照一定的逻辑关系进行分配,从上到下形成有序的逐阶分解。在学术研究和管理实践中,人们通过比较不同的组确定层次分析法中各个层次因素的相对重要性,然后通过综合判断与比较,判断各个因素的重要性和总体顺序。最终,经过研究和分析,得到各个影响因素的权重和候选对象的因素的分值,从而进行相关的评价。
如运用层次分析法分析企业营销资源力量化评价问题,结合实施企业内外的营销资源,可以构建企业营销资源力的评价指标体系,将灰色系统理论与层次分析法相结合,建立了企业营销资源力的灰色多层次评价模型。再如运用层次分析法对高速公路企业运营效益风险评价,可以将灰色理论和层次分析法结合起来,并对高速公路企业运营效益风险进行评价,得出评价结论。运用该模型对某省的高速公路企业运营风险进行评价,验证了此模型的正确性。结果表明,运用该模型可以对高速公路企业运营效益风险评价得更科学合理,该方法具有一定的使用价值,更可靠,可以让管理者对风险程度有清晰的认识。
动态规划是求解某类问题的一种方法,是考察问题的一种途径,而不是一种特殊算法,就目前而言,动态规划没有统一的标准模型,其解法也没有标准算法,在实际应用中,需要具体问题具体分析。在计划工作中,经常会碰到这样的问题,就是在人、财、物都有限的情况下,如何合理地利用有限的人力、物力、财力,以求达到最大的效率,最有效地实现预定的计划。这是一个统筹规划问题,用数学语言表达出来,就是在一组约束条件下,寻求一个函数的极大值和极小值的问题。比如,经济效益、利润、销量等我们希望越大越好——求极大值;成本、各种消耗等我们希望越小越好——求极小值。寻求的这个函数,我们称之为目标函数。当约束条件表现为线性等式或线性不等式,目标函数表现为线性函数,就属于线性规划问题。
2 企业管理中数学规划程序与风险
2.1 数学规划的程序
在企业管理的数学规划过程中,必须遵循先需求分析,后解决方案的程序。首先是分析企业在日常经营活动中的业务需求,在此基础上,将业务需求转换为相对应的数学规划需求,用数学的语言将相关的要求表达出来,然后,分析自身发展的数学规划需求以及需要获取的数据需求,最后,根据获得的资源和已经掌握的资料,针对企业的数学需求进行求解和运算,从而得出相关的理论结论,根据理论结论来指导生产。
2.2 企业管理实践中运用数学规划存在的风险
企业运用数学规划来辅助管理是一个涉及企业内部核心业务与各个业务之间配合的大系统工程。因此,在决策层面与实施层面上可能遇到各种各样的问题,形成数学规划风险。企业在运用数学规划进行辅助管理的过程中,必须认真识别到这些风险,并且采用相关的策略来规避风险。
(1)动机风险。数学规划能提高企业的管理效率,同时也能够提升企业的形象,增强企业管理的透明度,引进先进的管理模式。但是,因为企业管理的目标不同,数学规划会带来不同的动机。如果动机的方向性发生错误,必然会影响企业实际管理的效果,从而带来巨大的战略性风险。
(2)变革风险。数学规划是一种高效的、新兴的管理方法。信息技术和管理技术的不断发展推动了整个企业管理的方法论变革,从而使企业的经营管理理念发生了最为本质的改变。管理变革必然涉及企业各种主体的核心,其风险是必然的。因此,企业应该做好变革管理工作,从而降低变革风险。
(3)数据资料风险。数学规划对所掌握资料的来源要求比较高,一个错误的资料可能导致整个规划失败。因此,企业数学规划的技术方案确定后,即将面临的风险就是数据来源的掌握。企业必须保证数学规划所需要的数据资料保持完整性、真实性、全面性和有效性。
3 企业管理中数学规划应用实践
ABC公司是国内知名的服装企业,2009年1~4月,公司工业产值83470万元,制造出成品衣302667件,总销量304267件,营业收入78318万元,利润总额11799万元,超额完成了全年净增长5万件的任务以及公司曾提出的五年达到50万件的战略计划。

表1 公司2009年1~4月各月销售额
从表1中可以得知,第2、3月的市场销售较大,1、4月份的需求量较小,为很好的满足定货的需求,采用改变库存水平的方法,求出每月份的最优生产量,使之能正好完成1~4月定货的生产计划且使生产费用与库存费用总和最小。ABC服装企业1~4月销售额达到了250475400元,那么每月需要的费用为65128850元。
3.1 假设和约束条件
根据ABC服装公司市场营销的实际情况,在不影响制定的生产计划最优化并接近公司实际情况的前提下,设立如下假设:(1)年初、年终都没有存货;(2)市场营销人员工资、行程费、场地费等不存在制约因素;(3)市场销售足够满足每月定货量的要求,但是不超过16万件;(4)企业库存容量不超过10万件;(5)设dk为第k月产品的需求量;xk为第k月产品的生产量;vK为第k月开始时产品的库存量:ckxk为第k月生产产品时的成本费用,包括固定费用和产品成本;hkvk为第k月的库存费:ckxk+ hkvk为第k月产品的成本费;故状态转移方程为:Vk+1=Vk+XK-dK。
其中ak=min(vk+dk,m),m为每阶段生产的上限。边界条件为:f5(v5))=0,v5=0,v1=0;约束条件为

其中q为最大库存量,p为每月生产的最大能力。
3.2 模型的建立
把连续决策处理为离散决策,则可将ABC服装企业1~4月份每月的订货量列示出来。

表2 ABC服装企业2010年1~4月每月的市场销售量
依据ABC服装企业实际调查情况可知,每件衣服的出厂价为22.99元,第k月的生产成本为:
ckxk=m+1.025*l07xk,当0 当k=4时,有: 其中v4+x4-d4=v5,而v5=0,所以v4=8- x4; 当k=3时,有: 其中v3+x3-d3=v4,所以v3=23-x4; 当K=2时,有 当k=1时,有 其中v1+x1-d1=v2,所以v1=43-x4-x3-x2-x1 通过Matlab程序实现得到结果,由此可知,x1=13,x2=15,x3=15,x4=0,v1=0,v2=5,v3=8,v4=8,其中m=65118850(元),f1(v1)=6.80*108(元)。即最佳预计销售方案为:第一个月卖了13万件,第二个月卖了15万件,第三个月卖了15万件,第四个月最好卖4万件,总最低费用为6.80*108元。 数学规划在现代企业管理中扮演着不可或缺的角色,对企业的产品营销、市场、企业运营方面等问题都能提供较好的解决方案。本文在层次分析法和动态规划的基础上,运用实际数学模型,计算得出了ABC服装企业1~4月的预计市场销售量安排。通过对定量订货模型的理论探讨和实例验证,表明衣服销售量和盈利情况可以通过数学规划来进行优化,数学规划在企业的实际管理中承担了重要的任务,从量化的角度对企业管理决策提供了理论依据,使企业管理更加科学。 [1]马克M.戴维斯等.运营管理基础[M].北京:机械工业出版社,2005(7). [2]姜启源.数学模型(第二版)[M].北京:高等教育出版社,1993(8). [3]钱西汉,王成焘.AHP在动态联盟企业的盟员选择中的应用[J].机械设计与制造工程,2000(7).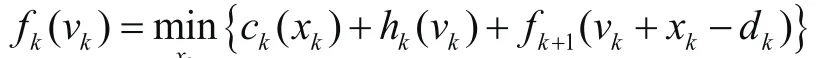
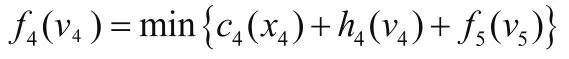
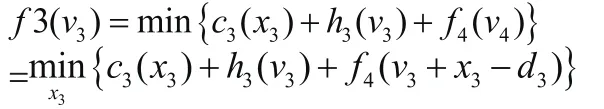

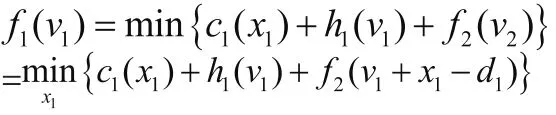
3.3 运算结果分析
4 结语

