基于水基系统的地区健康评价—以富锦市为例

纪 毅，付 强，邢贞相，姚 巍

（东北农业大学 水利与建筑学院，哈尔滨 150030）

0 引 言

水基系统是指在一定水文尺度和空间范围内，水及与其相关的涉水介质和涉水工程共同构成的基础生境承载系统，对流域而言，它涵盖了流域内水、气、生物、土壤、社会经济等诸多内容［1－2］。水基系统将与水有关联的事物综合到一个巨系统内，然后研究该系统的状态和承载力，这使得评价更具全面性、科学性和系统性。但是，目前对水基系统的研究尚处于初级阶段，相关研究较少并且很少有人应用于实例当中。周惠成等［3－4］基于水基系统概念提出了城市水基系统，证明了水基系统在进行健康综合评价时具有很好的效果。富锦市位于黑龙江省三江平原地区，是全国重要的产粮基地，近年来由于经济发展造成的环境破坏，对地区健康产生了影响，因此，本文应用水基系统对富锦市进行健康评价。

1 基于水基系统的地区健康评价指标

根据水基系统的定义，评价水基系统健康状态时，以3个特征属性来表征水基系统的状态：稳定性、和谐性、演进性，并分别用稳定态、和谐度和演进率对这3个特征属性加以描述。由于研究区域主要以农业为主，参考相关规范及文献 ［3～5］并结合研究地区的自然和社会特点，制定了稳定态评价指标及评价标准 （表1）、和谐度评价指标及评价标准 （表2）。演进率是对稳定态及和谐度的动态描述，因此，将演进率分为稳定态演进率及和谐度演进率，利用历年稳定态及和谐度的特征值绘制稳定态折点图和和谐度折点图，将过程线上点的斜率作为演进率特征值，演进率标准值见表3。

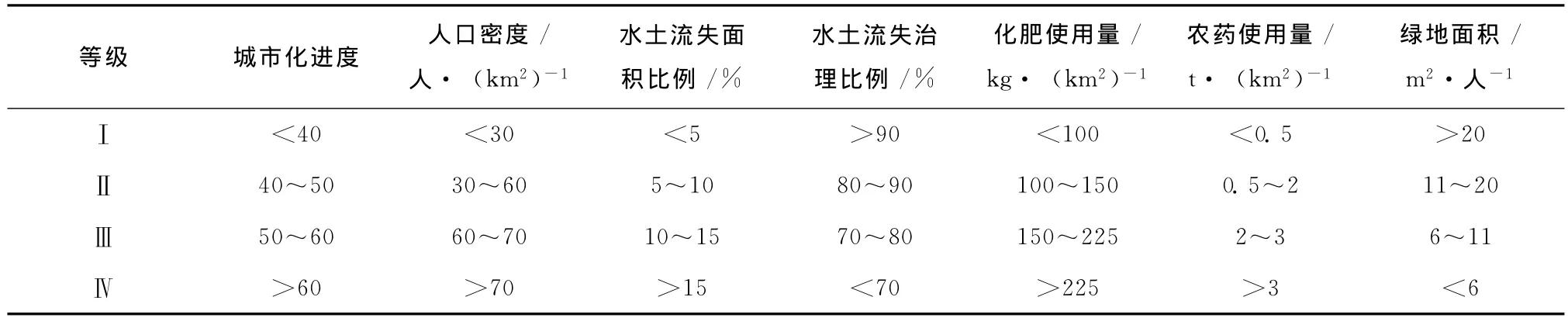
表1 稳定态指标及评价标准Table 1 Index and standard value of steady state

表2 和谐度指标及评价标准Table 2 Index and standard value of harmonious degree

表3 演进率标准值Table 3 Index and standard value of evaluation rate

2 水基系统健康的综合评价

Topsis模型是一种常用的有限方案多目标决策分析法［6－7］，又称逼近理想解排序法，它根据指标性质和数据，以一组最优指标数据作为虚拟正理想方案 （1），以一组最劣指标数据作为虚拟负理想方案 （2）：

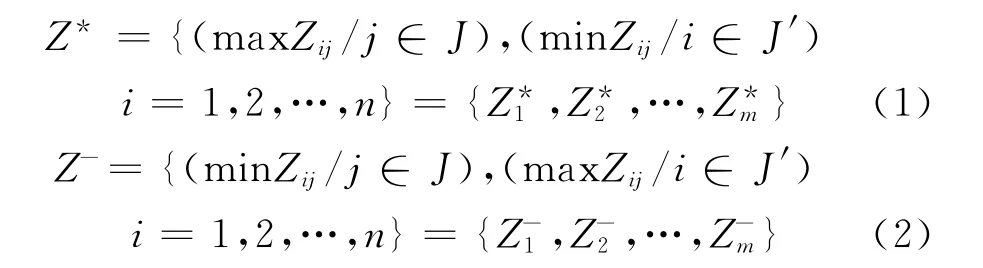
式中Zij为加权归一化矩阵中的元素，J、J′分别代表越大越优型指标集和越小越优型指标集。

通过计算实验点距正、负理想点的欧氏距离，通常采用欧几里德距离系数计算每个监测点到理想解的距离S＊i和到负理想解的距离S－i：

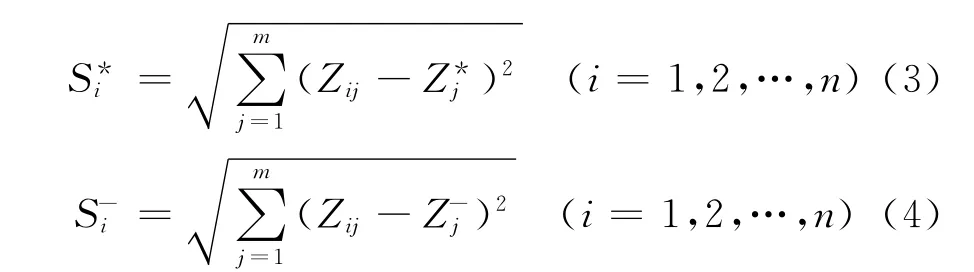
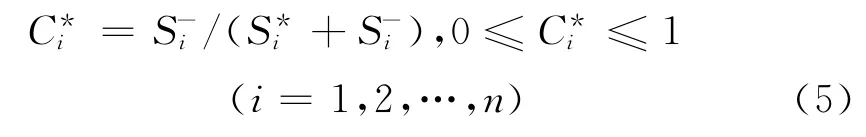
在运用Topsis模型进行水基系统健康评价时，首先应该确定水基系统稳定态及和谐度的特征值，然后通过两者的特征值求得演进率，最终通过稳定态、和谐度、演进率进行综合评价。

2．1 确定指标权重

目前，计算多指标综合评价中各指标权重的方法很多，如特尔菲法、层次分析法、均方差法、隶属频度法、主成分分析法等。熵权法能根据熵的概念和性质，充分挖掘数据本身所携带的信息，从而确定指标权重［8－9］，尽可能地避免主观意识带来的误差。通过熵权法计算得到稳定态指标及和谐度指标权重向量。

稳定态权重向量：αi＝ ［0．141 5 0．142 9 0．142 9 0．141 9 0．143 3 0．144 9 0．142 2］

和谐度权重向量：βi＝ ［0．124 3 0．126 1 0．123 8 0．127 6 0．124 7 0．123 9 0．126 2 0．123 3］

2．2 稳定态及和谐度评价

2．2．1 稳定态及和谐度等级特征值的确定

将表1、表2中的标准值建立矩阵，通过归一化处理，然后结合权重向量，得到加权归一化矩阵，最后计算得到各等级的欧式贴近度，即为稳定态及和谐度等级的标准值，见表4。

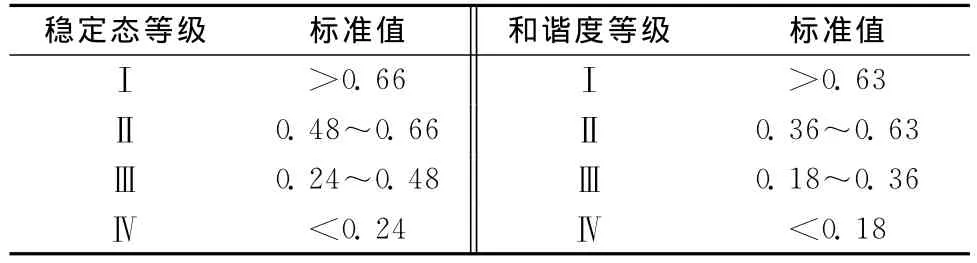
表4 稳定态及和谐的等级标准值Table 4 Grade standards of steady state and harmonious degree

2．2．2 稳定态及和谐度特征值计算

将研究区域的稳定态及和谐度指标值与标准值组成指标特征矩阵，带入Topsis模型，计算贴近度可得到富锦市2005～2009年的稳定态及和谐度特征值，然后通过与稳定态及和谐度等级特征值进行比较，得到富锦市2005～2009年稳定态等级及和谐度等级，见表5。

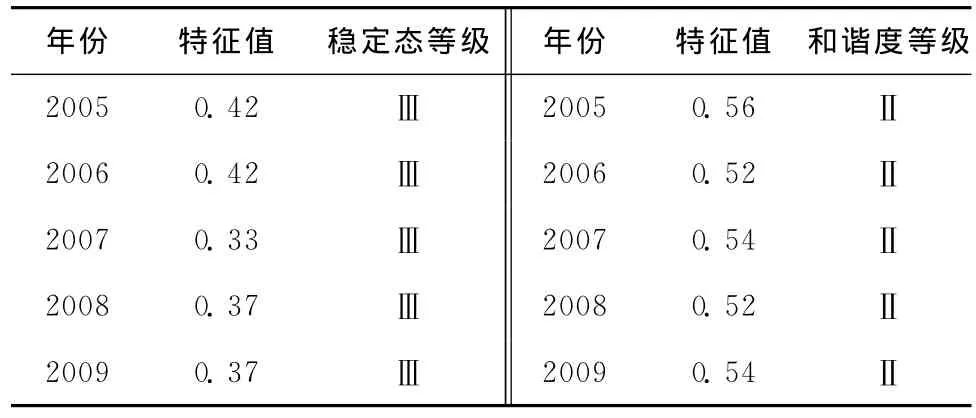
表5 稳定态及和谐度等级结果Table 5 Grades of steady state and harmonious degree

2．3 演进率评价

根据表5中的稳定态及和谐度特征值，计算2006～2009年的稳定态及和谐度演进率，结合表3中的演进率标准值，可以得到2006～2009年富锦市水基系统的演进率见表6。

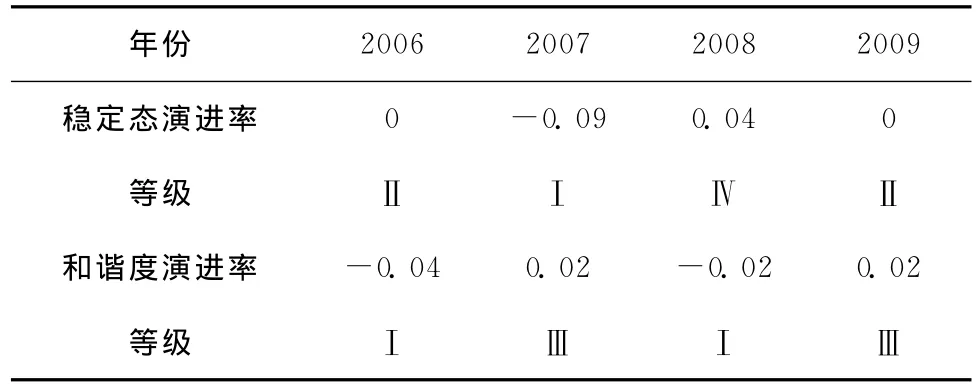
表6 演进率等级结果Table 6 Grades of evaluation rate

2．4 水基系统健康的综合评价

在分别对稳定态、和谐度和演进率分析的基础上，可以对富锦市水基系统的健康状况做出综合评价。根据研究区域的实际情况，对稳定态、稳定态演进率、和谐度、和谐度演进率权重进行分配，最终确定权重分别为0．40、0．10、0．40、0．10。另外，由于上述计算获得的演进率数值偏小，不能直接与稳定态、和谐度综合以获得评价结果，因此，需要对演进率进行归一化计算，然后进行综合评价。若评价值≥0．62时，系统处于健康状态；评价值在0．42～0．62间属于较健康状态，评价结果列于表7。

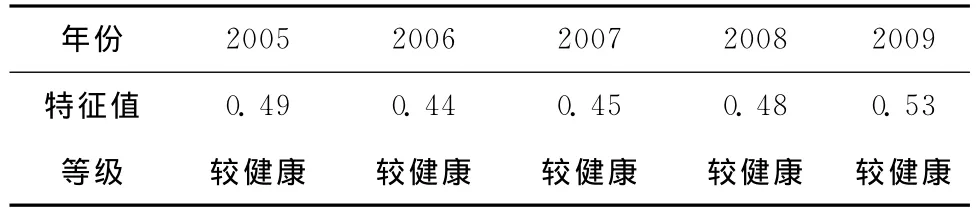
表7 富锦市水基系统评价结果Table 7 Assessment result of Fujin water－based system

2．5 评价结果分析

由表5可见：富锦市的稳定态在2005～2009年间处于Ⅲ级，造成稳定态较低的主要原因在于研究区域水量较少，导致饮水安全及用水量得不到有效保证，因此，当加大水资源开发力度时很容易造成水基系统的不稳定状态；和谐度的等级优于稳定态的等级，处于Ⅱ级，这主要是因为该研究区域主要以农业为主，对水基系统的改造和破坏相对较少，和谐度较高；水基系统的综合健康状态处于较健康状态，并且在2007年以后出现回升状态。

3 结 论

本文采用基于熵权法的Topsis模型对富锦市水基系统进行了健康综合评价，评价结果显示富锦市水基系统的健康状态相对较低，制约系统健康的关键因素是水基系统的稳定态较弱。富锦市水基系统健康状态提高的关键措施在于加大地表水控制力度、增加节水灌溉面积、提高工业污水处理率及重复利用率等。

［1］刘 宁．水基系统的概念内涵与演进研究 ［J］．水科学进展，2005，16 （4）：475－481．

［2］刘 宁，杜国志．集成水文技术解读水基系统 ［J］．水科学进展，2005，16 （5）：696－699．

［3］周惠成，丛方杰．大连市水基系统健康多目标模糊评价 ［J］．大连理工大学学报，2008，48 （5）：720－725．

［4］周惠成，丛方杰．基于指标权重可靠性分析的大连市水基系统评价 ［J］．辽宁工程技术大学学报，2008，27 （5）：770－773．

［5］向碧为，黄国如，冯 杰．基于AHP法的东江流域水基系统健康模糊综合评价 ［J］．水电能源科学，2011，29 （10）：1－4．

［6］胡永宏．对TOPSIS法用于综合评价的改进 ［J］．数学的实践与认识，2002，32 （4）：572－574．

［7］李春辉，李爱贞．TOPSIS法在环境质量综合评价中的应用 ［J］．地质灾害与环境保护，1992，11 （10）：33－35．

［8］潘竟虎，冯兆东．基于熵权物元可拓模型的黑河中游生态环境脆弱性评价 ［J］．生态与农村环境学报，2008，24 （1）：1－4．

［9］王艳芳．灌溉水质综合评价的熵权可拓模型 ［J］．灌溉排水学报，2009，28 （3）：73－76．