水泥混凝土强度推定的多参数模型应用研究
王正君,毛继泽,于雪峰,刘春花,王大智,陈 瑶
(1.黑龙江大学 水利电力学院,哈尔滨150080;2.中国地震局 工程力学研究所,哈尔滨150080;3.哈尔滨工程大学航天与建筑工程学院,哈尔滨150001;4.黑龙江大学 建筑工程学院,哈尔滨150080)
水泥混凝土强度是影响混凝土结构正常使用的一个重要因素,因此,应采用无损、快速的检测方法掌握其强度分布情况,并及时采取相应的处理措施,以保证其使用寿命[1-5]。而目前应用超声法评定混凝土板强度时主要是采用单参数的强度推定模型,检测精度较低。为提高水泥混凝土板强度推定的精度,本文开展了多参数强度推定模型的应用研究。
1 模型参数的引入
现在国内外报道的有关用超声声速对水泥混凝土质量信息进行反映的研究较多,而忽略了其他参数对水泥混凝土质量信息的反映。声波在一种物质中传送,或由一种物质传入另一种物质时,由于受到衰减,反射及折射的作用,其能量必然愈来愈弱。亦即声波在传输过程中能量是有衰减的,这种衰减的大小与水泥混凝土的组成材料和结构是直接相关的[6-15]。混凝土的强度综合地反映了上述质量情况,而描述这种衰减恰恰可以通过超声的相应参数来完成。
衰减系数与混凝土物性有着密切关系。在致密、强度高的混凝土中,声波衰减系数较小,波幅衰减慢;在强度低的混凝土中,声波衰减系数大,波幅衰减快。因此,有必要把波幅的变化考虑到强度推定模型中。在超声检测过程中,中心频率能表征声波传播过程的衰减,也能很好地反映相应质量信息。为此,对超声参数之一的频率与混凝土强度的关系也应进行系统的研究。
2 超声法检测混凝土多参数强度推定模型的建立
由于常用的单参数声速强度推定模型用指数型用得较多,那么引入衰减系数以后的数学模型是否也可以与单参数指数模型具有相类似的表达形式呢?为此,首先从平面运动方程出发,去探索双参数的模型形式。
通过平面波运动方程式 (1),分别求时间t和坐标x的两次偏导数可得平面简谐波的微分方程,见式 (2):

纵、横波的波动方程为式 (3)和式 (4):
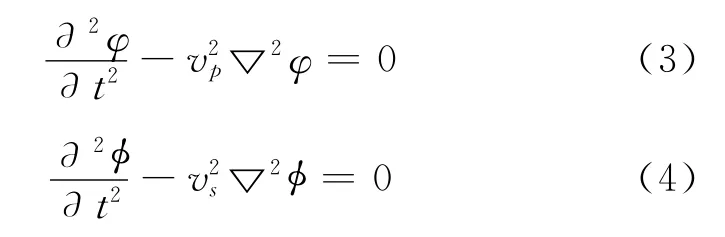
由于均匀介质中的x,y,z三维问题可简化为x,z二维问题来研究,所以式 (3)和式 (4)可写为式 (5)和式 (6):

式中C,B为与振源强度有关的系数;a,b为振幅衰减系数;k为波数。
由于式 (5)、式 (6)具有相同的表达形式[16],如z方向为一定值 (在一固定深度时),故可将其表示为式 (7):

可以将距离、速度及时间的关系式表示成为v(x,t)=x/t的形式[17],如x 为定值,则可写成式 (8):

由于强度的指数推定公式fcu=aeav,依据式(8)可将式 (7)中的fcu(t)写成为式 (9):

Tharmarntnam等研究认为推定强度和振幅可以使用式 (2~20):
后阴即肛门,为大肠的下口,又称魄门、谷道。魄门为粕之通道,魄门即粕门,饮食糟粕由此排出体外,所以称为魄门。

考虑到声压与衰减系数的表达式 (10),并且超声波探伤仪示波屏上的波高 (振幅)与声压成正比,即振幅Ar(x)=p/p0=e-ax。故可将式 (2~13)中的fcu(x)写成式 (11):

比较式 (17)、式 (19)、式 (10)和式 (11),则有式 (12):

根据以上的推导发现:在建立超声和混凝土强度的数学模型时,单一地考虑速度参数是不够的,还应考虑衰减。而衰减的表征既可以通过振幅来体现,也可以通过中心频率来体现。因为,声波的频率与混凝土物性也存在着密切关系。这是因为超声检测用的是脉冲波,含有多种频率成分。而混凝土的衰减系数α是频率的函数,频率越高衰减越快,并且脉冲波的高频成分容易衰减掉。当混凝土质量较差时,接收到的声信号中高频成分已损失掉,频率变低。既然强度与声速和振幅之间遵循式 (12),那么,强度与声速和频率之间是否也遵循类似的关系式呢?衰减系数一方面可用声压、振幅来体现,另一方面超声衰减与中心频率有密切关系。由前面分析可知,扩散衰减与声波传播的声程 (x)有关,故该数学模型可按照如下方法建立:由式 (12)及扩散衰减系数α(x)=1/f,故可用中心频率的变化来体现公式中的衰减项,得到式 (13)的数学模型:

在测量距离已知的情况下,得到式 (14):

基于以上分析,推定强度可能具有以上的两种表达式,那么是否具有如式 (15)、式 (16)的两参数及三参数的模型型式呢?

为书写及描述方便,将考虑声速和表征振幅衰减的衰减系数α1的强度推定模型式 (2~22)称为双参数模型I,并表示为式 (17):

将考虑声速和表征频率衰减的衰减系数α2的强度推定模型式 (13)称为双参数模型II,并表示为式 (18):

同时将考虑声速、衰减系数α1和衰减系数α2的强度推定模型称为三参数模型,并用式 (19)表示:

目前,对混凝土进行超声检测时,声时或声速用得较多,而对应的其他参数,如振幅、中心频率应用的研究却很少见。故本文开展了超声检测双参数、三参数强度推定数学模型方面的应用研究。
由前面分析过程得知,推定强度可应用式(9)、式 (10)、式 (11)进行,其中式 (9)用得很多,也很成熟;式 (10)和式 (11)用得较少,但回归分析过程和式 (9)一样,通过简单的变换就可以转换为一元线性回归,这里不再赘述。本文以式 (12)为例介绍二元非线性转化线性回归的分析过程。
对式 (12)两边取对数,得到式 (20):
ln fcu(x,t)=ln A+ln eBv(t)+ln eCα(x)(20)即ln fcu(x,t)=ln A+Bv (t)+Cα (x)。令y=ln fcu(x,t),x1=v (t),x2=α (x),得到b0=ln A,b1=B,b2=C,则式 (12)转化为式(21):

这样,式 (12)由二元非线性转换为二元一次回归计算。
3 水泥混凝土的多参数强度推定模型建立
为建立水泥混凝土的多参数强度推定数学模型,给出了该种水泥混凝土的配比及检测龄期见表1。
水泥混凝土试块数据处理见表2,表中声速取试块3点检测声时计算的均值,振幅与中心频率对应3点的均值;表中衰减系数I用α1表示,其计算将振幅单位dB转化为Np后,再除以测试距离15cm得到;表中衰减系数II用α2表示,其计算是将中心频率除以测试距离15cm得到。
混凝土抗压强度与超声声速的拟合曲线见图1,抗压强度与声速的指数曲线拟合的相关系数R=0.787,拟合的数学模型为式 (2~22):

水泥混凝土双参数模型I和双参数模型II的三维分析见图2和图3。
通过以上拟合建立的水泥混凝土的单、双及三参数强度推定数学模型见表3。从表3可以看出:水泥混凝土的双参数模型I和双参数模型II比单参数的强度推定模型相关系数略高,三参数模型与双参数模型I的相关系数相同。试验表明超声声速与混凝土的抗压强度相关性较好,振幅和中心频率虽然都与混凝土的抗压强度有一定的相关性,单只考虑二者和抗压强度时其相关性较差,但同时和声速两因素综合考虑时,相关性有一定的提高。所以在工程上可适当考虑两参数或三参数的强度推定模型。

表1 水泥混凝土配比及检测龄期Table 1 Mix proportion of cement concrete and testing age

表2 水泥混凝土测试数据Table 2 Testing data of cement concrete


图3 双参数模型II三维图Fig.3 Three dimensional graph of dualparameter model II of concrete

表3 强度推定数学模型及相关系数表Table 3 Strength speculation mathematical models and correlation coefficient
4 结 论
本文建立了双参数及三参数水泥混凝土抗压强度推定的数学模型。通过采用当地的自采材料,制作标准试件 (150mm×150mm×150mm),结合时域及频域曲线,得到相应的声参数,考虑到振幅与中心频率的衰减,得到其相应的衰减系数,以此建立不同强度等级的水泥混凝土双参数以及三参数的抗压强度推定的数学模型,并分别与用同样试块所建立的单一强度推定模型进行对比:双参数模型I、双参数模型II及三参数的抗压强度推定的数学模型的相关系数要比单一强度推定模型的相关系数要高。
[1]程朝霞,徐银芳,王毅翔.超声波法检测混凝土强度的发展 [J].华中科技大学学报:城市科学版,2003,20(4):95-98.
[2]Demirboga R,Turkmen I,Mehmet A B.Relationship between ultrasonic velocity and compressive strength for high-volume mineral-admixtured concrete [J].Cement and Concrete Research,2004,(34):2 329-2 336.
[3]Kewalramani M A,Gupta R.Concrete compressive strength prediction using ultrasonic pulse velocity through artificial neural networks [J].Automation in Construction,2006,(15):374-379.
[4]Chang T P,Lin H C,Chang W t,et al.Engineering properties of lightweight aggregate concrete assessed by stress wave propagation methods [J].Cement & Concrete Composites,2006,(28):57-68.
[5]Akhras N M.Detection freezing and thawing damage in concrete using signal energy [J].Cement and Concrete Research,1998,(28):1 275-1 280.
[6]Prassianakis I N,Prassianakis N I.Ultrasonic testing of non-metallic materials:concrete and marble [J].Theoretical and Applied Fracture Mechanics,2004(42):191-198.
[7]Del R L M,Jimenez A,Lopez F,et al.Characterization and hardening of concrete with ultrasonic testing[J].Ultrasonics,2004,(42):527-530.
[8]吴庆曾.论声参量波幅的应用 [J].岩土工程界,2000,(3):9-12.
[9]Gudra,Stawiski B.Non-destructive strength characterization of concrete using surface waves [J].NDT&E International,2000,(33):1-6.
[10]韩建刚,赵伟封,郑南翔.灌注桩的超声检测研究[J].铁道建筑,2002,(10):3-5.
[11]Lee H K,Lee K M,Kim Y H,et al.Ultrasonic in-situ monitoring of setting process of high-performance concrete[J].Cement and Concrete Research,2004,(34):631-640.
[12]缪 群,李为杜.硅灰高强混凝土超声测强及影响因素研究 [J].无损检测,1999,21(8):356-358.
[13]童寿兴,李为壮.高强、超高强混凝土的超声测强技术研究 [J].施工技术,1993,(3):412-413.
[14]琚晓辉,马荣贵,孙建民.水泥混凝土路面厚度超声检测系统 [J].公路,2005,(8):125-128.
[15]傅竹武,胡家富,温一波,等.混凝土路面强度与厚度无损检测的超声模拟 [J].云南大学学报:自然科学版,2000,(22):54-60.
[16]王 辉,张青山.公路工程地质勘探使用技术 [M].北京:人民交通出版社,2004:254-284.
[17]Liang M T,Wu J.Theoretical elucidation on the empirical formulae for the ultrasonic testing method for concrete structures [J].Cement and Concrete Research,2002,(32):1 763-1 769.

