1.5岁大通牦牛公牛体重与体尺指标的相关回归分析

王 伟

(青海省大通种牛场，青海 西宁 810102)

大通牦牛是中国农科院兰州畜牧与兽药研究所和青海省大通种牛场培育成功的牦牛新品种[1]。对大通牦牛体尺与体重相关性分析未见报道。然而研究牦牛体重与体尺的相关与回归在大通牦牛上有着很重要的意义。在以往的畜牧兽医工作中，无论是品种资源调查、选种选配，或者是计算日粮、考虑用药量等等，都需要了解牛的体重。实称牛的体重一般不易做到，尤其是在牧区更难做到，但根据牛的体尺来估算牛的体重是可靠易行的简便方法。在实际工作中发现，如把每个年龄段的样本合在一起分析，体重与体尺的相关系数差异性不显著，说明不同的年龄和性别体重与体尺的相关系数也有差异，为此按年龄和性别分别进行分析，旨在为以后实际工作中估测体重把误差控制在最小的范围内。

1 材料与方法

1.1 材料来源与样本

青海省大通种牛场2011年11月测定31头大通牦牛1.5岁公牛。体重是空腹进行称重。为了便于描述，将体重、体斜长、体高、胸围、管围5个指标用下列大写字母代替，分别为TZ、TXC、TG、XW、GW。

1.2 统计方法

所得数据采用Spss17.0程序Pearson和Linear过程[5]进行处理。

1.2.1 Pearson相关系数分析计算模型

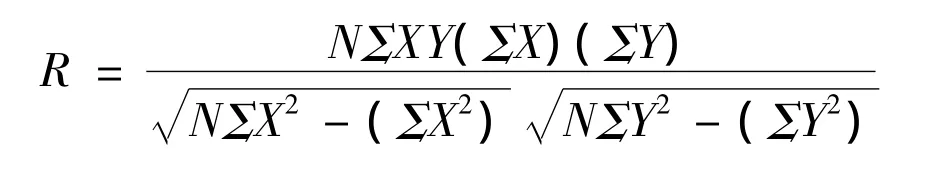
式中，R为Pearson相关系数，数值介于-1～1之间。当R值为正数时为正相关，表示依变量随自变量的增大而增大;当R值为负数时为负相关，表示依变量随自变量的增大而减小;当R值等于0时表示依变量与自变量之间没有相关性。X为自变量，Y为依变量。

1.2.2 多元线性回归分析计算模型

Y=b0+b1X1+b2X2+…+bn+Xn，其中Y为依变量，b0为常数、b1，b2+…bn，为回归系数，X1，X2，…Xn，为回归系数对应的自变量。

2 结果与分析

2.1 相关分析

设TXC、TG、XW、GW的值作为自变量，TZ的值作为依变量。

2.2 回归分析

分别采用 Linear过程 “Enter”法和“Stepwise”建立多元线性回归方程，统计结果见表2和表3。

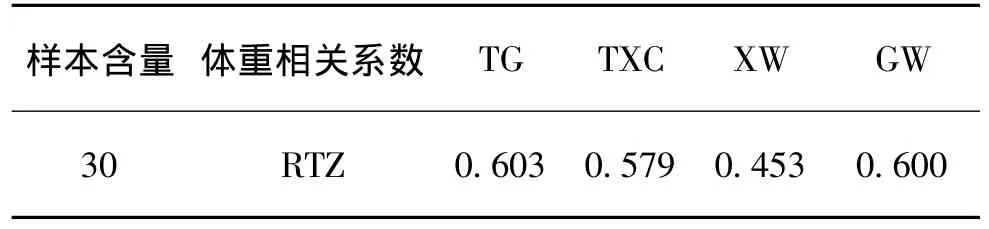
表1 相关系数统计结果

表2 回归模型系数

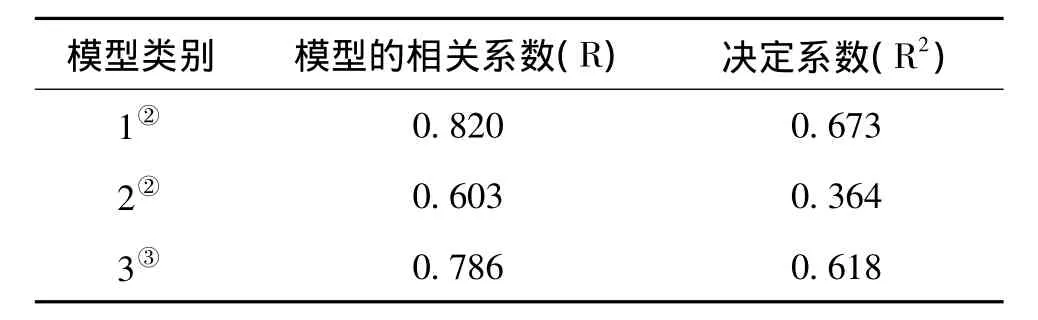
表3 回归模型拟合度综述①

从表2可知，这3个回归模型分别为:

第1个回归模型:TZ=-126.519+1.297×TG+0.643×TXC+0.316×XW+6.586×GW

第2个回归模型:TZ=-126.519+2.499×XW

第3个回归模型:TZ=-194.740+2.134×XW+7.945×TXC

从表1中可以看出，这3个回归模型的相关系数 R分别为0.820、0.603、0.786，拟合度的决定系数 R2值分别为0.673、0.364、0.618，说明线性度较好，尤其第1个回归模型拟合度的决定系数R2值就更高，线性度更好。

3 讨论

3.1 通过分析大通牦牛体高、体斜长、胸围、管围4个指标与体重之间的相关系数，分别为0.603、0.579、0.453、0.600，说明大通牦牛1.5岁公牦牛体高、体斜长、胸围、管围之间存在显著正相关。这与穷达、薛长安的研究结果一致。

3.2 该研究表明得到了3个估测大通牦牛1.5岁公牦牛体重的回归模型。表明大通牦牛1.5岁公牦牛体重与体高、体斜长、胸围、管围存在明显的线性关系，在实际应用中可根据各回归模型的R2值大小以及体尺测量的繁琐程度来对3个模型进行选择。其中最简单的模型是TZ=-126.519+2.499×XW

3.3 大通牦牛1.5岁公牛体重与体尺指标的相关回归分析模型在实际生产中具有重要的意义。牦牛是放牧型动物，活动范围较为广，对其称重较为不便，然而在畜牧兽医工作中，无论是品种资源调查、选种选配，或者是计算日粮、考虑用药量等都需要了解牛的体重，测量牦牛体尺，通过体重与体尺的回归模型测算牦牛体重是比较方便可行的方法。

[1] 陆仲璘，何晓林，阎萍.世界上第一个牦牛培育新品种-“大通牦牛”简介[P].中国草食动物“大通牦牛”新品种培育及其培育技术论文集2005:12-14.

[2] 马存寿.杂种牛荷斯坦成年母牛体重与体尺指标的相关回归分析[J].青海畜牧兽医杂志，2012(1):28-29.

[3] 田亚磊，朱东亮，张聪，等.太行黑山羊体重、体重的相关性分析 [J].山西农业科学，2009(5):31-32.

[4] 凌莉.生物统计学基础 [M].北京:人民卫生出版社，2010:130-135.

[5] 穷达，彭措巴姆.西藏嘉黎成年母牦牛体重与体尺指标的相关回归分析 [J].畜牧与饲料科学，2011，32(6):11-12.