缓冲材料参数对核废料处置库近场影响的二维有限元分析

秦爱芳， 赵 飞， 赵小龙

(上海大学土木工程系，上海200072)

缓冲材料参数对核废料处置库近场影响的二维有限元分析

秦爱芳， 赵 飞， 赵小龙

(上海大学土木工程系，上海200072)

以高放射性核废料地质处置的FEBEX原位试验作为数值计算模型，利用有限元软件Code-Bright，通过改变膨润土初始渗透系数、初始吸力和初始进气值，得到热-水-力(thermo-hydro-mechanical，THM)耦合作用下处置库关闭后缓冲层饱和度和吸力的变化规律，以及以上3个因素对这些性状影响的敏感程度，研究结果可为核废料处置库缓冲材料的选取提供参考．

膨润土;核废料处置库;热-水-力耦合;数值模拟

Abstract:The FEBEX in-situ test for geological disposal of high-level radioactive nuclear waste is used as a calculation model．By changing the initial permeability，the initial suction and the air entry value，variation of saturation，and suction under the coupled thermo-hydro-mechanical(THM)action are analyzed using a Code-Bright program after the closure of nuclear waste repository．By analyzing sensitivity of the three parameters on these traits，valuable reference is presented for the selection of buffer materials of the nuclear waste repository．

Key words:bentonite;nuclear waste repository;coupled thermo-hydro-mechanical(THM);numerical simulation

高放射性核废料是通过深埋于适当的岩石、盐或粘土层并使用人工屏障隔离核废料来达到安全处置的目的，其中作为缓冲/回填材料的膨润土由于具有较高的膨胀性、极低的渗透性和优良的核素吸附等性能，常被用作存放核废料的铜罐和周围岩石之间的人工隔离屏障［1］．处置库投入运营后，一方面库内核废料衰变放热导致处置库周围缓冲/回填材料产生温度应力;另一方面由于围岩高压力水头的作用使周围岩石内水向膨润土发生渗透，从而导致高压实的、富含蒙脱石的膨润土的饱和度持续上升，并产生膨胀应力．这样的隔离屏障在热量和水的作用下会产生非常复杂的“热-水-力(thermo-hydromechanical，THM)”现象，并且它们之间相互关联耦合．

为了确保这个隔离屏障的长期安全性，有必要研究这种耦合现象的作用机理．目前，一些发达国家已经对此进行了许多试验和理论研究工作．以原位试验为例，有瑞士的“FEBEX”原位试验、美国的尤卡山试验、瑞典的“原型仓库”试验、德国高勒本地下试验室等项目．

1985年，中国开始针对高放核废料处置展开了一系列实质性的研究，如甘肃北山预选区花岗岩场的选址和场址评价研究［2-3］．2006年初，国家相关部门颁布《高放废物地质处置研究开发规划指南》［4］．2007年，国家颁布的《核电中长期发展规划》中明确提出了到2020年前建成处置高放核废料的地下试验室、到21世纪中叶建成高放废物处置库的目标［5］，而其中所涉及的THM耦合作用机理的研究尚处于起步阶段．为此，许多学者正在对此进行积极而有意义的探索．

刘月妙等［6］采用有限差分计算程序 FLAC2D，考虑热-力耦合，模拟在不同处置室间距的条件下，高放废物处置库的温度场、应力场和位移场规律．张玉军［7-8］研制出了用来分析饱和孔隙介质中THM耦合弹塑性问题的二维有限元程序，并对FEBEX原位试验进行了数值模拟，以及通过改变初始水头、初始渗透系数和初始饱和度对缓冲层饱和过程的影响进行了二维有限元分析．Millard等［9］对围岩中核废料处置库近场THM耦合进行了数值模拟分析，得出应力对THM耦合影响很大．Lee［10］利用数值模拟和现场调查的方法研究了加拿大高放核废料地质处置室围岩的热-力学稳定性．Abel等［11］采用Van Genuchten模型，通过试验和数值模拟的方法研究了MX-80膨润土干密度、温度和含水量与吸力的变化规律等．

高放核废料处置库中，作为缓冲/回填材料的膨润土的主要的功能是，遇水吸湿引起饱和度的上升，并导致土体发生膨胀变形(主要发生在膨润土靠近周围岩石部分)，以密封膨润土在砌置时形成的块体之间和块体与周围岩石之间的施工缝隙，以及周围岩石因处置库开挖卸载引起的裂缝，进而直接影响核素的迁移．影响膨润土饱和度、吸力的诸多因素中，初始渗透系数、初始吸力及初始进气值比较关键，因此，本研究选用适当的热、水、力本构方程及平衡方程，采用Code-Bright软件［12］对处置库近场进行THM数值模拟，得到处置库近场膨润土饱和度和吸力的变化规律，以及初始渗透系数、初始水压及初始进气值对其影响的敏感程度．

1 热-水-力耦合模型

1．1 水质量、能量及力学平衡方程［13-14］

本研究的基本控制方程为水质量守恒、能量守恒以及静力平衡方程．

1．1．1 水的质量守恒方程

水的质量守恒方程为

式中，θl和θg分别表示单位体积液相中水的质量和单位体积气相中水(水蒸气)的质量，Sl和Sg分别表示液相和气相的饱和度，φ为空隙率，fw为单位体积介质中外界提供的水的质量，jwl和jwg分别表示液相和气相中水流动的质量．jwl和jwg分别由以下几部分组成:

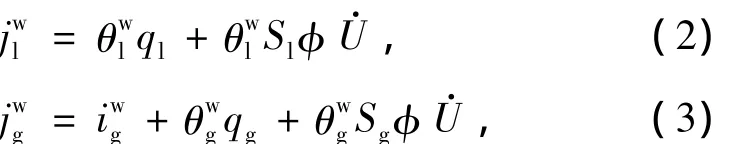
式中，ql和qg分别为液相和气相的Darcy流动(相对于固相)，U·为固相的速度，iwg为气相中水蒸气的扩散．

1．1．2 能量守恒方程

能量守恒方程为

式中，Es，El和 Eg分别为固、液、气三相的比内能;ρs，ρl和 ρg分别为固、液、气三相的密度，其中液相和气相的能量Elρl和Egρg又可表示为

fE为单位体积介质中外界提供的能量;ic为热传导能量;jEs，jEl和jEg分别表示三相相对于固定参照系的热对流能量，具体由以下几部分组成:

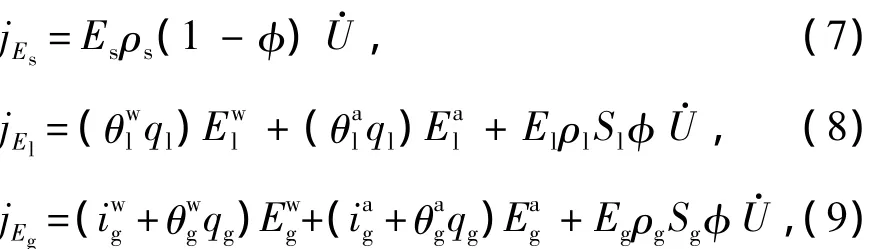
其中iag为气相中空气的扩散，θal和 θag分别表示单位体积液相中和气相中空气的质量．

1．1．3 静力平衡方程

忽略惯性力的静力平衡方程为

式中，σ为应力状态向量;b为体力向量．对于饱和多孔介质，力学本构方程引入有效应力概念，即

式中，mT=(1，1，1，0，0，0)．对于非饱和多孔介质的本构方程，通常引入两个独立的应力状态量，即净法向应力σ－pgm以及基质吸力s=pg－pl，其中pg为气压力，pl为水压力．

1．2 热本构方程

本研究假定热传导服从Fourier定律，即

式中，ic为介质导热量;T为介质温度的微分;λ为热传导系数，表征材料导热性能的物性参数(λ越大，导热性能越好)．显然，λ和三相热传导系数λs，λl，λg，空隙率以及饱和度有关，具有如下关系式:

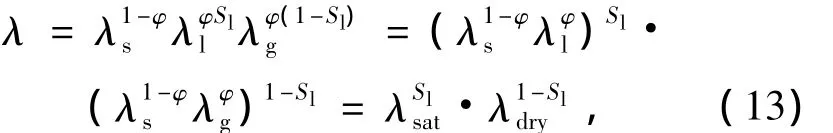
式中，Sl为土的饱和度，λdry，λsat分别为完全干燥和完全饱和状态下土的热传导系数．

1．3 流体本构方程

本研究假定孔隙中液相、气相遵循Darcy定律，即

式中，ql，qg分别为液相和气相的流量;Ki为液相或气相渗透系数张量(Ki=kriK/μi，i为l或g)，其中kri为液相或气相相对渗透系数;g为重力向量;K为介质固有渗透系数;Δpl，Δpg分别为水压力和气压力的梯度;ρl，ρg分别为液相和气相的密度．

与以上计算有关的参数表达式如下．

(1)固有渗透系数K与孔隙率直接相关，固有渗透系数为

式中，φ0为参考孔隙比，K0为对应于φ0的固有渗透系数．

(2)液相相对渗透系数为

式中，A为常数;n为指数，通常取为2～4;Se为有效饱和度，Se与实际饱和度Sl之间的关系为

式中，Slr为液相残余饱和度，Sls为液相最大饱和度．

(3)饱和度与基质吸力的关系．

为了建立起液相饱和度与基质吸力之间的联系，反映非饱和土滞留水的能力，较常见的 Van Genuchten模型的表达式为

式中，P=P0σ/σ0，P0为参照温度下的进气值，σ0为参照温度下的表面张力;P和 σ为计算温度下的进气值和表面张力;β为形状参数．

1．4 力学本构方程

目前有关非饱和土的应力应变本构模型很多，但能较好反映非饱和土相关力学参数的模型有非线性弹性模型和巴塞罗那模型．本研究采用非线性弹性模型［14］，该模型体积应变的计算采用以下关系式:

式中，p 为净平均应力，a1，a2，a3为无量纲参数，s=Pg－Pl为基质吸力．剪切应力应变关系为线性，剪切模量为G．本模型假设基质吸力的变化只引起体积应变．

2 有限元数值分析

2．1 计算模型［15］

本算例采用FEBEX原位试验模型．FEBEX原位试验场位于瑞士的阿尔卑斯山脉，海拔1 725 m，其埋深约450 m．基岩为由花岗岩和片麻岩等组成的结晶质岩类．该试验处置坑道水平的直径为2．4 m，长18．8 m(见图1)．水平轴向放置两个加热器，其直径为0．9 m，长为 4．54 m．加热器周围填充缓冲/回填材料膨润土．加热器最初提供恒定的热量1 200 W，直到靠近加热器的膨润土左边界达到所需的最高温度100℃;然后控制加热器中的热量使膨润土左边界的最高温度保持100℃恒定不变;3年后(1 095 d)断掉热源，6个月冷却期(1 278 d)后拆除热源．

初始条件设定为缓冲材料和坑道回填完毕，此时膨润土和岩石的初始温度均为12℃，初始各向应力分别为28．0 和 0．5 MPa，初始水压分别为 －97．2和0．5 MPa，初始气压均为 0．1 MPa．岩体是饱和介质，膨润土的初始饱和度是0．46，其中岩体、膨润土的主要参数如表1所示．

图1 FEBEX原位试验近场模型图(m)Fig．1 Layout of FEBEX in-situtest(m)

表1 主要计算参数Table 1 Main computation parameters

考虑试验布局的对称性和影响范围，取处置库轴对称模型试验，即从单个热源中心向外依次为加热器、缓冲层(膨润土)和岩石(见图2)．模型的边界条件如下:左边界在水平方向加约束;上、下边界在垂直方向加约束;右边界由于耦合作用影响的效果不明显，所以径向应力、水压和温度取恒定值，分别为28 MPa，0．5 MPa和12℃．本研究重点对以下3个部位进行分析，从左向右依次是:加热器附近膨润土(节点238)、膨润土中部(节点239)、靠近岩石的膨润土(节点240)，其中共有180个四边形等参数单元，273个节点．

2．2 初始渗透系数的影响

假定膨润土的初始渗透系数分别为2×10－15，2 ×10－13和2 ×10－11m/s，初始进气值为 50 MPa，初始饱和度为 0．46，初始吸力为 97．3 MPa，计算至1 278 d时加热器周围膨润土中三点的饱和度-时间曲线和吸力-时间曲线如图3和图4所示．

图3 不同初始渗透系数下饱和度-时间曲线Fig．3 Saturation degree-time curves for different initial permeabilities

图4 不同初始渗透系数下吸力-时间曲线Fig．4 Suction-time curves for different initial permeabilities

由图3可见，当初始渗透系数较大时，3个部位的饱和度均随时间变化较小;当初始渗透系数较小时，3个部位的饱和度变化差异均较大．随着初始渗透系数逐渐减小，膨润土饱和度达到某一稳定值所需的时间将延长．对于节点238的膨润土，当初始渗透系数较小时，其饱和度随时间急剧减小至某一值后达到相对稳定，并基本维持不变．断开热源后(即1 095 d后)进入冷却期，饱和度略微回升;对于节点239的膨润土，不同初始渗透系数的条件下，其饱和度随时间变化不大，且随初始渗透系数的减小，达到相对稳定后膨润土的饱和度略有降低;对于节点240的膨润土，当渗透系数较小时，饱和度随时间逐渐增大至一定值后达到相对稳定．断开热源后(即1 095 d后)进入冷却期，饱和度略微回落．

由图4可见，对于节点238的膨润土，随着初始渗透系数逐渐减小，吸力逐渐增大;对于节点239的膨润土，其吸力随时间先减小后增大至某一值后达到相对稳定;对于节点240的膨润土，其吸力随时间逐渐减小并很快达到某一相对稳定值．当初始渗透系数较小时，对节点238的膨润土吸力影响较大，而初始渗透系数的大小对其他两个部位影响不是很明显．

2．3 初始吸力的影响

假定膨润土内的初始吸力分别为117．3，97．3和 77．3 MPa，对应的初始饱和度分别为 0．40，0．46和0．58，初始进气值为50 MPa，初始渗透系数为2×10－13m/s，计算至1 278 d时加热器周围膨润土中三点的饱和度-时间曲线如图5所示．

由图5可见，初始吸力不同则初始饱和度不同．对于节点238的膨润土，初始吸力的大小对其达到稳定后的饱和度影响不大．饱和度随时间急剧锐减至某一值后达到相对稳定，断开热源后(即1 095 d后)进入冷却期，饱和度略微回升;对于节点239的膨润土，初始吸力的大小对饱和度变化的影响是相近的，随着初始吸力逐渐减小，相对稳定后所能达到的饱和度逐渐增大;对于节点240的膨润土，初始吸力的大小对饱和度变化的影响也是相近的，饱和度随时间逐渐增大到一定值后达到相对稳定．断开热源后(即1 095 d后)进入冷却期，饱和度略微回落，而在相对稳定后所能达到的饱和度随初始吸力的减小而增大．

2．4 初始进气值的影响

假定膨润土的初始进气值分别为20，50和80 MPa，初始吸力为97．3 MPa，初始渗透系数为2×10－13m/s，计算至1 278 d时加热器周围膨润土中三点的饱和度-时间曲线如图6所示．

图5 不同初始吸力下饱和度-时间曲线Fig．5 Saturation degree-time curves for different initial suction

图6 不同初始进气值下膨润土内饱和度-时间曲线Fig．6 Saturation degree-time curves for different initial air entry value

由图6可见，对于节点238的膨润土，饱和度随时间急剧锐减至一定值后达到相对稳定．断开热源后(即1 095 d后)进入冷却期，饱和度略微回升;对于节点239的膨润土，其饱和度随时间先增大后略微减小至某一值后达到相对稳定;对于节点240的膨润土，饱和度随时间逐渐增大至一定值后达到相对稳定，断掉热源后(即1 095 d后)进入冷却期，饱和度略微回落．以上3个点的初始进气值越小，初始饱和度及饱和度稳定后的值也越小．

3 结论

(1)高放核废料处置中膨润土饱和度受初始渗透系数、初始吸力和初始进气值影响较大．

(2)当初始渗透系数较大时，3点的饱和度及吸力变化均不大．当初始渗透系数较小时，靠近加热器处的膨润土，其饱和度及吸力受初始渗透系数影响最大，饱和度随时间急剧减小至某一值后达到相对稳定，进入冷却期后饱和度略微回升，其吸力值却逐渐增大;中间处的膨润土，其饱和度随时间略有降低随后相对稳定，其吸力随时间先减小后增大至某一值后达到相对稳定;靠近岩石处的膨润土，其饱和度随时间逐渐增大至一定值后达到相对稳定，进入冷却期后饱和度略微回落，其吸力随时间逐渐减小并能很快达到某一相对稳定值．

(3)初始吸力越小，初始饱和度越大．靠近热源及岩石处膨润土的初始吸力的大小，对饱和度变化影响较大．靠近热源处的膨润土，其饱和度随时间急剧减小到某一值并保持相对稳定，进入冷却期后饱和度略微回升，初始吸力的大小对其达到稳定后的饱和度没有影响;中间处的膨润土，其饱和度随时间变化不大，初始吸力的大小对饱和度变化影响很小;靠近岩石处的膨润土，其饱和度随时间增大到某一值并保持相对稳定，进入冷却期后饱和度略微回落．随初始吸力的逐渐减小，相对稳定后所能达到的饱和度逐渐增大．

(4)以上3个点的初始进气值越小，初始饱和度及饱和度稳定后的值也越小．

［1］ 孙文静，孙德安，闫威．侧限应力状态下非饱和膨润土的变形特性［J］．上海大学学报:自然科学版，2010，16(1):105-110．

［2］ 徐国庆．2000～2040年我国高放废物深部地质处置研究初探［J］．铀矿地质，2002，18(3):160-167．

［3］ 王驹，范显华，徐国庆，等．中国高放废物地质处置十年进展［M］．北京:原子能出版社，2004:13-26．

［4］ 国防科学技术工业委员会，科学技术部，国家环境保护总局．高放废物地质处置研究开发规划指南［Z］．2006．

［5］ 王驹．高放废物深地质处置:回顾与展望［J］．铀矿地质，2009，25(2):71-77．

［6］ 刘月妙，王驹，蔡美峰，等．热-力耦合条件下高放废物处置室间距研究［J］．铀矿地质，2009，25(6):373-378．

［7］ 张玉军．热-水-应力耦合模型及FEBEX原位试验二维有限元分析［J］．岩土工程学报，2007，29(3):313-318．

［8］ 张玉军．三个因素对缓冲层饱和过程影响的二维有限元分析［J］．岩土力学，2006，27(6):853-857．

［9］ MILLARD A， REJEB A， CHIJIMATSU M， et al．Numerical study of the THM effects on the near-field safety of a hypothetical nuclear waste repository—BMT1 of the DECOVALEX Ⅲ project．Part 2:Effects of THM coupling in continuous and homogeneous rocks［J］．International Journal of Rock Mechanics＆ Mining Sciences，2005，42:731-744．

［10］ LEE C F．Thermo-mechanical stability of rock around a nuclear waste disposal vault［C］ ∥ International Conference on Computational Methods in Structural and Geotechnical Engineering．1994:82-90．

［11］ ABEL C J，MARÍA V V，GÓMEZ-ESPINA R，et al．Adaptation of the Van Genuchten expression to the effects of temperature and density for compacted bentonites［J］．Applied Clay Science，2009，42:575-582．

［12］ OLIVELLA S， GENS A， CARRERA J． Numerical formulation for a simulator(Code-Bright)for the coupled analysis of saline media［J］．Engineering Computations，1996，13:87-112．

［13］ OLIVELLA S， CARRERA J， GENS A， et al．Nonisothermal multiphase flow of brine and gas through saline media［J］．Transport in Porous Media，1994，15:271-293．

［14］ RUTQVIST J，BORGESSON L，CHIJIMATSU M，et al．Thermohydromechanics of partially saturated geological media;governing equations and formulation of four finite element models［J］．International Journal of Rock Mechanics＆ Mining Sciences，2001，38:105-127．

［15］ GENS A， GARCIA-MOLINA J， OLIVELLA S， et al．Analysis of a full scale in situ test simulating repository conditions［J］．International Journal for Numerical and Analytical Methods in Geomechanics，1998，22:515-548．

Two-Dimensional FEM Analysis of Near Field Influence of Buffer Material Parameters on High Level Radioactive Nuclear Waste Repository

QIN Ai-fang， ZHAO Fei， ZHAO Xiao-long
(Department of Civil Engineering，Shanghai University，Shanghai 200072，China)

TU 443

A

1007-2861(2012)05-0539-06

10．3969/j．issn．1007-2861．2012．05．018

2011-00-00

秦爱芳(1966～)，女，副教授，博士，研究方向为岩土力学与工程．E-mail:qinaifang@shu．edu．cn