非均布荷载作用下路面结构力学响应计算

顾 浩，魏为成

(1.江苏省交通科学研究院股份有限公司;2.招商局重庆交通科研设计院有限公司)

在现行路面设计规范中，将车辆荷载等效为圆形均布荷载，但事实上，车辆轮胎与路面之间的接触压力非常复杂。一方面，首先，车辆载荷是通过轮胎传递给路面的，而轮胎作用于路面的接地形状并不完全表现为圆形，相反，它更大程度上表现为矩形，而且轮胎荷载越大，接地形状越接近于矩形;其次，荷载大小均匀分布的假设离实际情况相差甚远，车辆荷载的增减以及轮胎胎压的变化都会造成分布情况的不同，尤其当车辆负载超过额定载荷或(和)轮胎胎压较大时，轮胎与地面的接触压力就会呈明显的非均匀分布形式;此外，轮胎的胎面是有花纹存在的，而且花纹的形式各种各样，花纹的这种多样和复杂性，决定了荷载作用分布的非均布性和接触形状的复杂性。另一方面，正是由于荷载分布的非均匀特性，它对路面结构层的力学影响就表现出很大的不同，特别是当非均匀分布越明显时，引起路面结构的力学响应与均布荷载所引起的力学响应的差别就会越大。因此，为了分析非均布荷载作用下的沥青路面结构力学响应，根据现有的一些数据资料，选取标准车型和典型路面结构，对非均布荷载作用下沥青路面结构的力学响应进行有限元计算。由于沥青路面的裂缝、车辙、松散等路面早期损坏，可能是由剪切应力引起的，至少是剪应力主导的一种剪切疲劳损坏或一次性剪切破坏，因而以路面结构的最大剪应力反应值作为主要分析对象。

1 计算参数的确定

1.1 计算车型及参数

计算选取我国公路路面设计规范的基准车型黄河JN150重型货车为标准，具体参数如表1所示。

表1 标准车辆参数表

1.2 轮胎接地面积

根据已有研究资料，荷载作用于路面的接地形状更接近矩形，因此假设荷载作用面积为矩形。由于轮胎胎面存在花纹，轮胎与地面之间非完全接触，因而实际的有效接地面积是接触总面积的折减，文献认为，纵向花纹的折减系数为75%～80%，横向花纹的折减系数为70% ～75%。在计算分析时考虑了轮胎花纹的因素，通过轮胎接地面积的长度反映。对黄河JN150重型货车横向花纹轮胎，将接地长度折减为75%，但总作用面尺寸保持不变。折减后的荷载分布形式如图1所示，图中阴影部分为荷载作用位置。同时为了便于比较，后面的部分计算中，也计算了荷载接地面不折减的情形，此时，荷载作用面形式仍如图1所示，只是荷载在作用面内全分布。

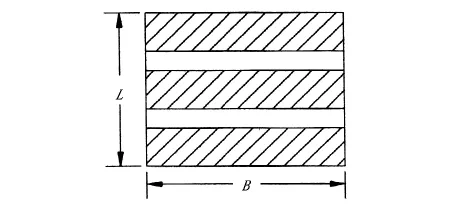
图1 荷载作用面积折减示意图

1.3 接地压力分布

研究表明，车辆荷载的增减以及轮胎胎压的变化都会造成分布情况的不同，导致荷载分布形式接近于凹型或凸型分布。为此，将荷载分布形式按如下三种假定:均匀分布;凹型分布，最高值为最低值的2倍;凸型分布，最高值仍是最低值的2倍，分别如图2(a)、(b)、(c)所示。对凹、凸型分布，其P值、0.75P值、0.5P值的作用宽度各占轮胎接地宽度的1/3，且对称于轮胎的宽度中心。

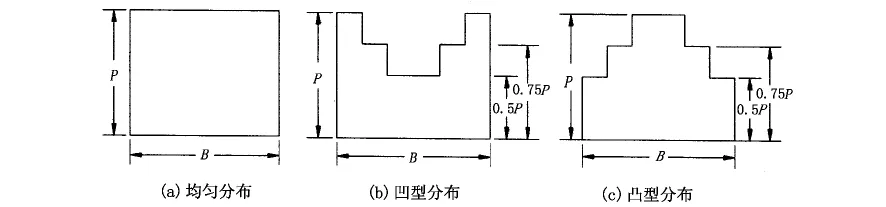
图2 荷载分布示意图

1.4 路面结构及参数

计算选取典型的高速公路路面结构，相关计算参数见表2所示。

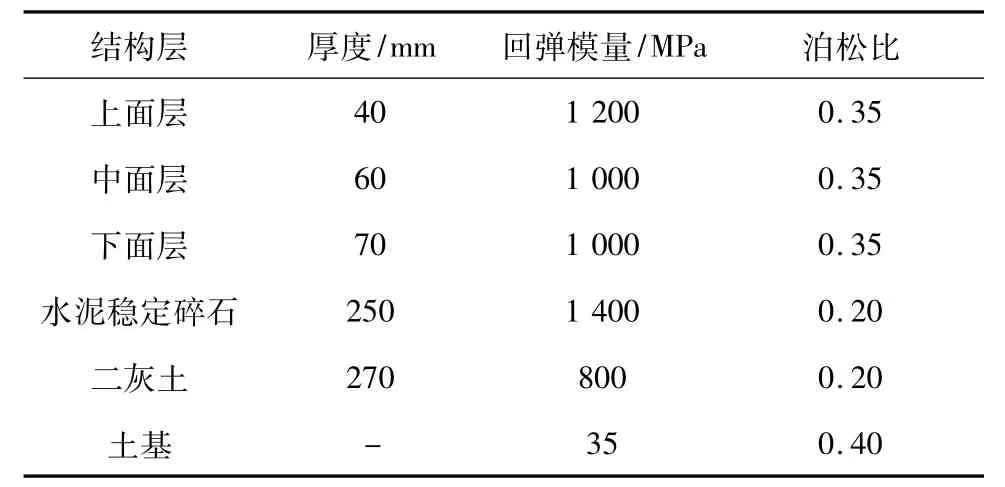
表2 路面结构计算参数

1.5 有限元计算模型

根据数据，建立的三维路面结构有限元计算模型如图3所示，其中，x、y轴方向分析范围各为2.5 m，z方向深度需依据理论弯沉值的大小进行调整。计算采用C3D20R单元，边界条件假设为左右两侧x方向位移为零，前后两侧y方向位移为零，底面z方向位移为零，层间接触条件为完全连续。

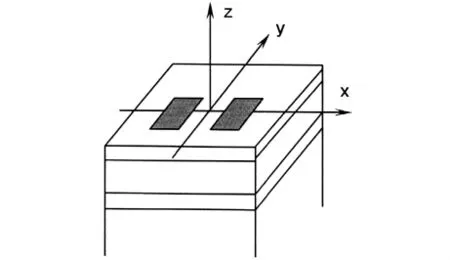
图3 有限元计算模型

2 非均布荷载作用下的路面力学响应分析

在考虑荷载分布的非均匀性时，轮胎总荷载不变，即总荷载大小是不变的，仅考虑荷载作用面积的折减，分为折减0.75%、不折减及荷载作用力的凸型、凹型、均匀分布三种分布形式。具体的荷载作用尺寸及大小如表3所示，以表2的路面结构作为计算分析对象。

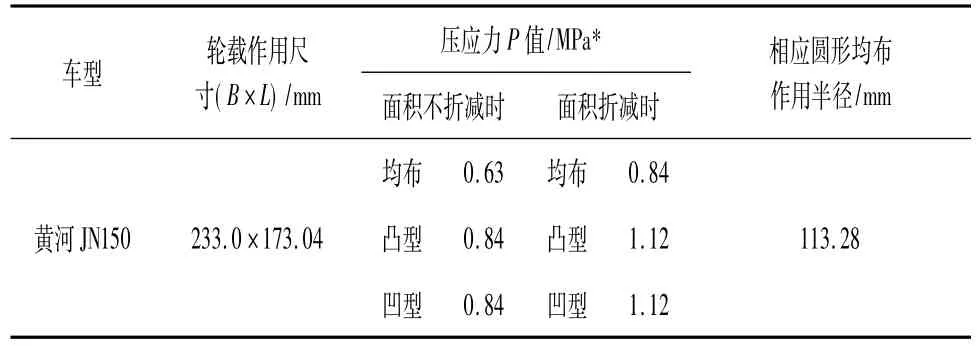
表3 荷载作用尺寸及作用力参数表

将以上的计算参数输入通用的有限元计算程序，计算结果见表4。

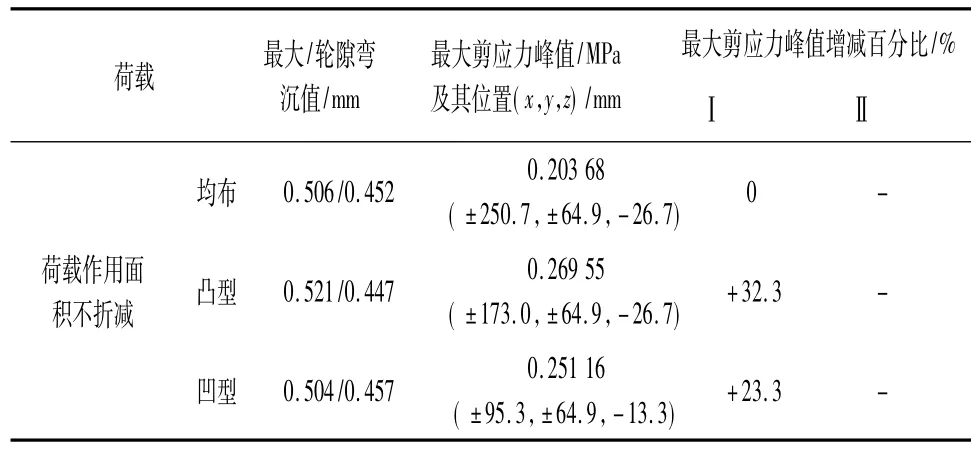
表4 不同荷载作用面积和不同分布形式下的计算结果

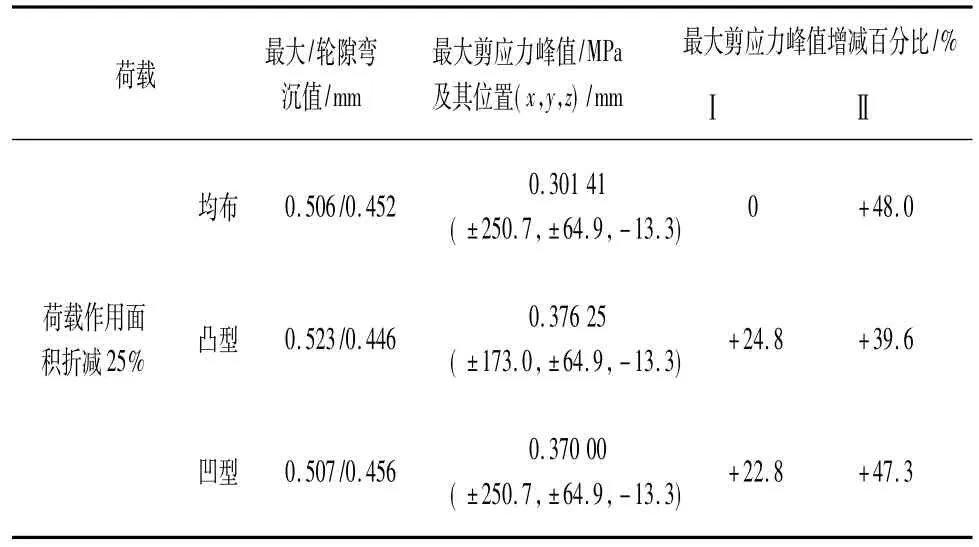
续表4

从表4结果可以得到以下结果:

(1)荷载的非均匀分布对弯沉的影响不大，在轴载相同的情况下，无论荷载作用面积是否折减或如何进行分布，最大弯沉及轮隙弯沉值基本不变。

(2)荷载的非均匀分布对路面结构最大剪应力峰值的影响很大，非均匀分布时的最大剪应力峰值，不论是凸型分布还是凹型分布，都比均匀分布时明显要大，增幅最高达32.3%。峰值的出现位置均处于上面层，但在深度和水平面上会随着荷载分布不同而有所改变。

(3)荷载作用面积的折减对最大剪应力峰值的影响也很大，考虑面积折减时的值要比不折减时最高增加48.0%;同时，峰值的出现位置会随着荷载分布不同而有所改变。

3 路面结构层模量变化时的力学响应分析

在非均布轮载作用下，对路面结构层模量变化对路面力学响应的影响规律进行分析。计算采用的车型参数如表1;依据有关资料，分别调整半刚性基层模量和面层的模量，得到的组合情况如表5和表6所示，计算时采用的泊松比也列于表中。

表5 半刚性基层模量变化时计算路面结构的各层模量组合

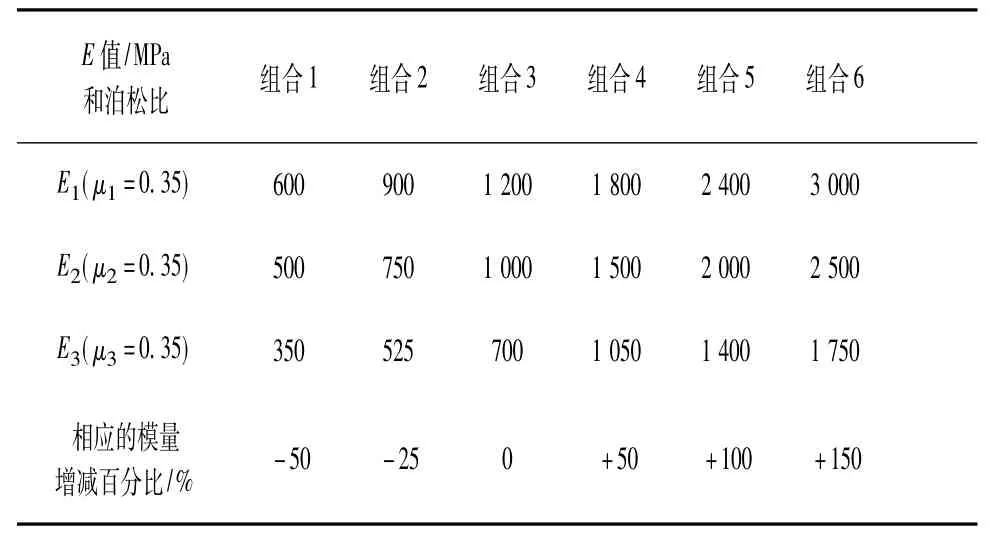
表6 面层模量变化时计算路面结构的各层模量组合

将相应的计算参数输入有限元程序进行计算，结果如图4和图5所示。

由图可以得到以下结论:

(1)随着半刚性基层模量的增加，最大剪应力峰值增大(最高增幅达31.37%)，而最大弯沉值减少，且均呈现出明显的非线性关系。

(2)随着面层模量的增加，最大剪应力峰值和最大弯沉值都减少，且均呈现出非线性关系。

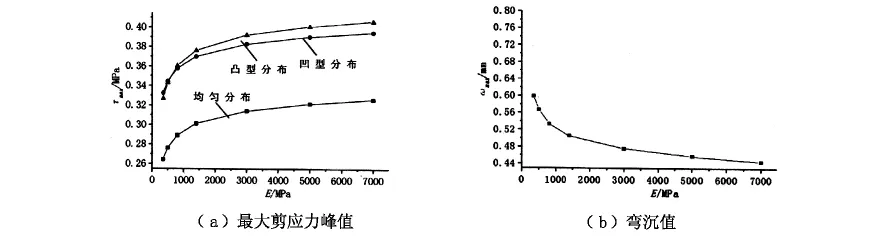
图4 半刚性基层模量变化时最大剪应力峰值及弯沉值响应图

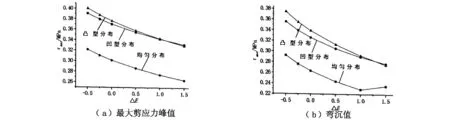
图5 面层模量变化时最大剪应力峰值及弯沉值响应图

(3)当半刚性基层的模量值较小时，如图4中各图所示模量值在350～1 500 MPa时，最大剪应力峰值及弯沉值的变化幅度较大，而当模量在较大值的范围内变化时(如＞1 500 MPa时)，最大剪应力峰值及弯沉值的变化幅度相对比较平缓，不过此时最大剪应力峰值的数值较大。

(4)虽然轮载分布形式不同对路面结构最大剪应力峰值的影响是大不相同的，但各种分布对峰值影响的变化趋势是基本一致的。

4 结语

(1)轮胎与路面的接触压力具有明显的非均匀分布特性，相对于均匀分布的轮载作用力而言，非均布荷载下路面结构内的最大剪应力变大，而且超载越严重，这种非均布特性越明显，从而导致路面结构受到的最大剪应力作用更大。

(2)随着半刚性基层模量的增加，路面结构的最大剪应力峰值增大，这说明过分强调半刚性基层的刚度，会导致路面结构、特别是面层受到剪切作用的破坏。

(3)随着面层模量的减小，路面结构的最大剪应力峰值增大，这说明在温度较高时，沥青混凝土的回弹模量较小，受到的剪应力较大，而此时沥青混合料的抗剪强度又是最低的，因而半刚性基层路面结构在夏天更易损坏。

[1]孙立军.沥青路面结构行为理论[M］.北京:人民交通出版社，2005.

[2]庄继德.汽车轮胎学[M］.北京:北京理工大学出版社，1997.

[3]催胜明，余群.汽车轮胎行驶性能与测试[M］.北京:机械工业出版社，1995:20-47.

[4]陆金燕.轮胎接地面三向力的动态测量[J］.橡胶工业，1992，(10):609-614.

[5]酒井秀男，管建民译.关于橡胶以及轮胎接触压力分布的测定和图象处理研究[J］. 橡胶工业，1995，(11).

[6]中华人民共和国行业标准.公路沥青路面设计规范(JTJ D50-2006)[S］.北京:人民交通出版社，2006.

[7]中华人民共和国行业标准.城市道路设计规范(CJJ37-90)[S］.北京:中国建筑工业出版社，1993.