反常积分敛散性的新对数判别法
赵建华
(上海海事大学,上海200135)
函数的定积分,有两个重要的约束条件,即积分区间的有限性和被积函数的有界性。将这两个约束条件取消,便得到了定积分两种形式的推广:(1)将函数的积分区间由有限扩展到无限就得到了无穷限的反常积分;(2)将被积函数由有界扩展到无界就得到无界函数的反常积分[1-3]。但是,反常积分涉及到一个所谓的收敛性问题。因为积分区间的有穷性和被积函数的有界性在很多实际问题中往往需要突破这些限制,因而对反常积分敛散性的判定就显得格外重要[4-15]。本文讨论的重点就是关于反常积分敛散性的新的对数判定方法以及新的对数判别法和旧的对数判别法的优劣。
1 研究内容
考察无穷限积分的对数审敛法[4]的证明知道,它是以反常积分1时收敛,p≤1时发散)作为标准来进行判定的。在本文的研究中,我们可以以反常积分(p>1时收敛,p≤1时发散)作为比较标准来探讨相应的判别法。类似地,对于瑕积分(a是唯一的瑕点),我们拟用(p>1时收敛,p≤1时发散)作为比较标准来探讨相应的判别法。
2 反常积分敛散性新的对数判别法
2.1 相关定理及其证明
定理1设函数f(x)为定义在区间[3,+∞)上的正值函数。
(i)如果存在常数λ>1及G>3,使得对任意的 x>G,有,则无穷限反常积分收敛。

即有
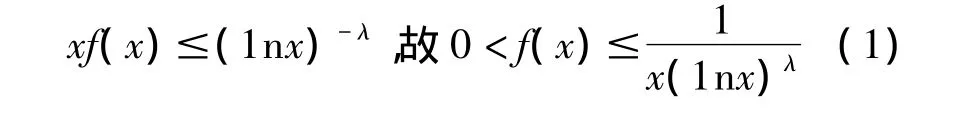
由于λ>1,故无穷限反常积分

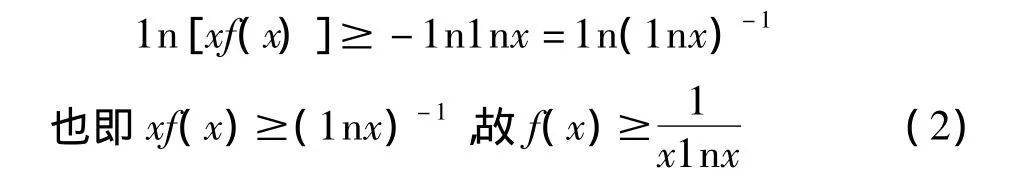
证毕。
定理1有如下极限形式:
推论1设函数f(x)为定义在区间[3,+∞)上的正值函数,且
由此可推出 1n[xf(x)] ≤1n(1nx)-(λ-ε),即有 xf(x)≤(1nx)-(λ-ε)。

当λ=+∞时,对M=2,存在G>3,使得对任意的 x>G有,即有
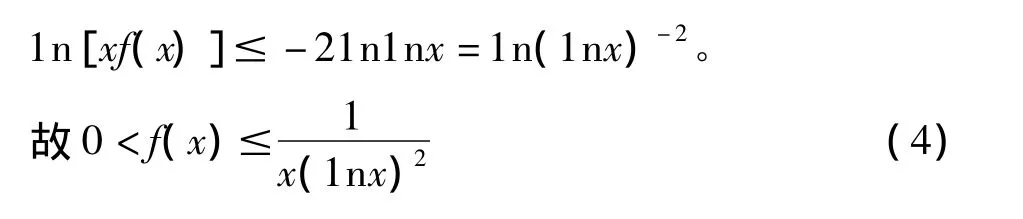

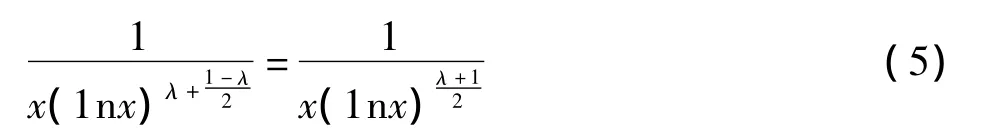
2.2 新旧对数判别法的比较
定理2设函数f(x)为定义在区间[3,+∞)上的正值函数。
(i)如果存在常数λ>1及G>3,使得对任意的x>G时有,则存在常数 λ'>1及G'>3,使得对任意的 x > G'时有≥λ'。
证明 (i)由于G>3,故当时x>G,有1n1nx>1nx>0。于是当 x>G时,假设,由于从而,对 λ >1,∃G'>3,当 x>G'时,有取λ'=λ,即得(i)的证明。
(ii)由于G>3,故当x>G时有1n1nx>1nx>
证毕。
证明 由定理2的证明过程知本推论成立,证毕。
3 瑕积分敛散性新的对数判别法
3.1 相关定理及其证明
定理3设函数f(x)为定义在区间(a,b] 上的正值函数,在点a的任一右邻域上无界,且在任何区间[μ,b] ⊂(a,b)上可积。
(i)如果存在 δ∈(0,e-1)及常数 λ >1,使得对于任意的 x∈(a,a+δ)有

(ii)若存在 δ∈(0,e-1),使得对于任意的 x∈(a,a+ δ)有
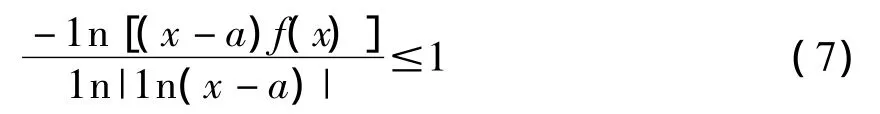
证明(i)因为0 < δ< e-1,故对于任意 x∈(a,a+δ)有0<x-a<e-1,于是 1n(x-a)< -1,故|1n(x-a)|>1,从而1n|1n(x-a)|>0。于是由式(6)可得
1n[(x-a)f(x)] ≤ -λ1n|1n(x-a)|=1n|1n(x-a)|-λ,即有(x-a)f(x)< |1n(x-a)|-λ,于是
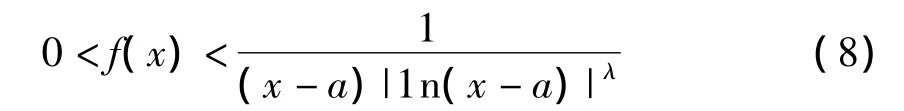
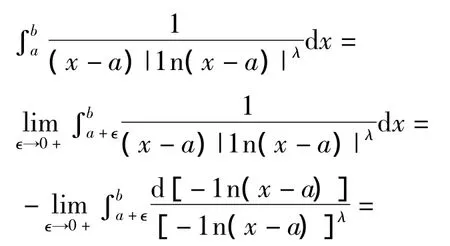

(ii)因为0 < δ< e-1,故对于任意的 x∈(a,a+δ),由于0<x-a<e-1,于是1n(x-a)< -1,故|1n(x-a)|>1,从而 1n|1n(x-a)|>0。由式(7)得1n[(x-a)f(x)] ≥ -1n|1n(x-a)|=1n|1n(x - a)|-1,即有
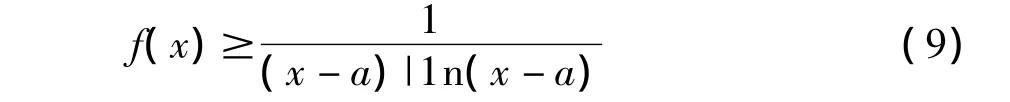

证毕。
定理3有如下极限形式:
推论3设函数f(x)为定义在区间(a,b)上的正值函数,在点a的任一右邻域(a,a+δ)上无界,且在任何区间[μ,b] ⊂(a,b)上可积。若,则

当 λ =+∞时,存在0 < δ<e-1,使得当 x∈(a,a+δ)时有从而1n[(xa)f(x)] <21n|1n(x-a)|。

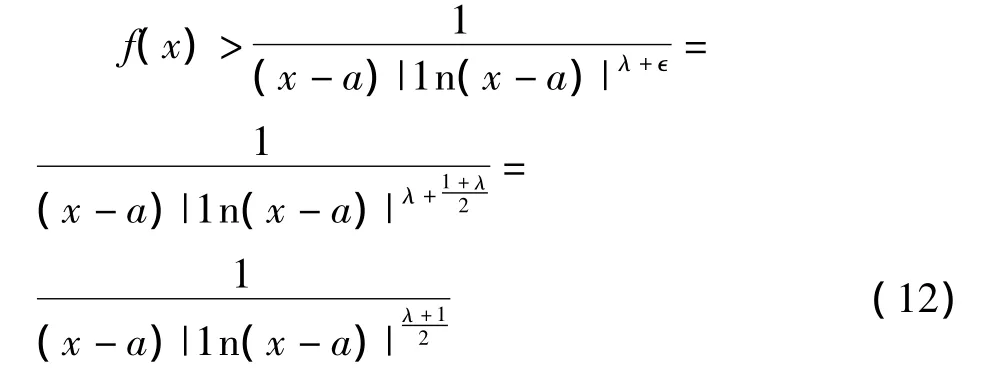
3.2 新旧对数判别法的比较
定理4设函数f(x)为定义在区间(a,b)上的正值函数,在点a的任一右邻域上无界,且在任何区间[μ,b] ⊂(a,b)上可积。
(i)如果存在 δ∈(0,e-1)及常数 λ∈(0,1),使得对于任意的 x∈(a,a+δ)时有,则存在 δ'∈(0,e-1)及常数 λ'> 1,使得对任意的 x∈(a,a+δ)有
(ii)如果存在 δ∈(0,e-1),使得对任意的 x∈(a,a+δ)时有,则存在 δ'∈(0,e-1),使得对任意的 x∈(a,a+δ'),有


即得(ii)的证明。
证毕。
推论4设f(x)是定义在(a,b] 上的正值函数,在点a的任一右邻域(a,a+δ)上无界,且在任何区间[μ,b] ⊂(a,b)上可积,若则
考察定理3的证明过程知,本推论成立,证毕。
[1] 同济大学应用数学系.高等数学(第5版)[M] .北京:高等教育出版社,2002.
[2] 华东师范大学数学系.数学分析[M] .北京:人民教育出版社,2001.
[3] 裴礼文.数学分析中的典型问题与方法[M] .北京:高等教育出版社,1993.
[4] 毛一波.反常积分与无穷级数的对数审敛法[J] .重庆文理学院学报,2007,4(1):25 -27.
[5] 陈亚丽.广义积分散敛性的对数判别法[J] .安徽电子信息职业技术学院学报,2004,3(5):113-114.
[6] 郭祖胜.非负函数无穷积分散敛性的新判别法[J] .三峡大学学报,2001,5(3):71 -72.
[7] 崔令霞.一种无穷限广义积分与正项级数的敛散法[J] .洛阳师范学院学报,2006,2(5):55-57.
[8] 边亚明.广义积分敛散性的一种判别法[J] .沈阳工程学院院报,2006,3(6):23 -25.
[9] 徐献瑜,冷生明.微积分学教程(第二卷)(第八版)[M] .北京:高等教育出版社,2006.
[10] 何忆捷.对一类反常积分收敛判别题的研究[J] .高等数学研究,2005,10(6):7 -8.
[11] 华东师范大学数学系.数学分析(上册)[M] .北京:高等教育出版社,2000.
[12] 陈传璋.数学分析[M] .北京:高等教育出版社,1983.
[13] 吉米多维奇.数学分析习题集题解(二)[M] .济南:山东科技出版社,1999.
[14] G KLAMBAUER.数学分析[M] .长沙:湖南人民出版,1981.
[15] HALLENBECK D J,TKACZYNSKA K.The absolute and uniform convergence infinite improper integrals[J] .Amer.Math.Monthly,1988(95):124 -126.
[16] HARUKI H,HARUKI S.Euler's integrals[J] .Amer.Math.Monthly,1983(90):464 -466.

