加速功率型电力系统稳定器参数整定方法研究

侯玉强，李威，胡剑琛，邢涛，马覃峰

（1.国网电力科学研究院，江苏南京210003；2.海南电网公司，海南海口570203；3.贵州电网公司电力调度控制中心，贵州 贵阳550002）

电网互联使得系统规模逐步扩大，远距离、大容量输电格局以及高顶值倍数励磁系统的广泛应用，导致系统的低频振荡问题日益凸显，甚至成为限制电网传输能力的瓶颈[1]。电力系统稳定器（PSS）作为发电机励磁系统的附加辅助环节，通过调节励磁输入产生阻尼转矩，是抑制系统低频振荡，提高系统小干扰稳定及动态稳定最简单有效的手段[2-3]。目前，PSS在系统中得到普遍应用，是现代励磁系统不可缺少的功能之一。

以发电机转速偏差Δω和电磁功率偏差ΔPe为输入信号的加速功率型PSS[4-5]，可计及发电机机械功率变化，被认为可避免机组有功出力快速下降时的无功反调现象[6-8]，因此近年来在系统中应用日益广泛。然而，某实际电网一起机组停机事故的录波数据表明，即使是加速功率型PSS，在参数整定不合理情况下仍可能出现无功反调现象。因此，有必要研究典型PSS参数对无功反调的影响；再者，目前PSS参数整定研究主要针对单输入信号型PSS[9-11]，而以加速功率型PSS为代表的双输入信号型PSS参数整定仍主要通过现场实验或仪器测试的方法反复尝试[12-14]，迫切需要研究利用数字仿真手段整定PSS参数的方法。

1 加速功率型PSS原理

加速功率型PSS的典型传递函数框图如图1所示。其中，Δω、ΔPe为双输入信号；Ts1为惯性环节时间常数，以模拟采样或信号转换导致的延迟，一般取0.02 s；Tw1~Tw4为隔直时间常数；Tp1～Tp6为超前滞后时间常数；Ka为PSS增益；Ks为功率匹配系数，通常取1.0；Kp、Tp分别为补偿系数及电磁功率积分时间常数；Tp8、Tp9为陷波器时间常数，主要用于过滤轴系扭振和噪声，通常取Tp8=0.2 s，Tp9=0.1 s。

根据式（1）所示的发电机转子运动方程，可知发电机转速偏差Δω表达式，如式（2）所示。

图1 加速功率型PSS传递函数框图Fig.1 Transfer functions of accelerating PSS

式中，M为发电机惯性时间常数；s为微分算子，ΔPm、ΔPa分别为发电机机械功率偏差和加速功率偏差。

忽略阻尼D，并将ΔPm通过G（s）函数以过滤轴系扭振和噪声，整理后得：

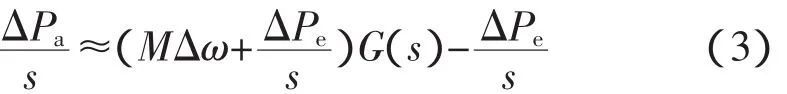
由式（3）可知，加速功率的积分正比于转速偏差Δω′，其表达式如式（4）所示。

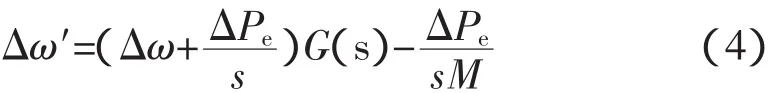
通过对Δω′的相位进行校正，可使补偿后的励磁系统提供正阻尼。由式（4）可知，与仅以ΔPe作为输入信号的功率型PSS相比，加速功率型PSS计及了发电机机械功率变化。因此，普遍认为加速功率型PSS可有效抑制无功反调。

2 PSS参数对无功反调作用的影响分析

我国某实际电网发生的一起机组停机事故中，因磨煤机故障，机组出力大幅快速下降。期间由于机组PSS动作，造成发电机无功功率（或电流）增加，机端电压上升。停机事故过程中发电机有功功率、电流及频率曲线如图2所示。

为了在不明显降低PSS阻尼特性的前提下，尽量减小无功反调作用，同时为PSS参数整定提供方向性指导，本文通过时域仿真方法，以机组汽门快关故障为例，详细分析了典型PSS参数变化对无功反调作用的影响。下述分析中每次仅改变PSS的某一参数而保持其他参数不变。

2.1 输入信号对无功反调作用的影响

图2 某实际电网停机事故过程中发电机有功功率、电流及频率响应曲线Fig.2 Responses of power，current and frequency during generator fast valving

加速功率型PSS可通过设置信号开关INP灵活选择输入信号。仅采用发电机转速偏差Δω作为输入信号时，汽门快关过程中发电机有功功率及无功功率响应曲线如图3所示。

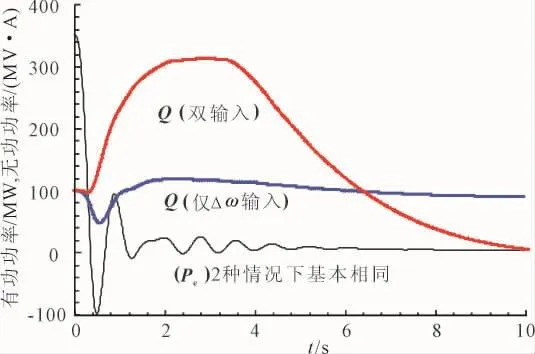
图3 采用不同输入信号时发电机有功及无功功率曲线Fig.3Generatorpowerandreactivepowerresponsesduring fast valving under different PSS input signals

可见，若能在事故后紧急闭锁电磁功率输入，可有效降低因机组出力大幅快速下降造成的无功反调，且对PSS阻尼效果影响不大。

2.2 增益对无功反调作用的影响

理论上讲，增益Ka越大，PSS提供的正阻尼越强，抑制系统低频振荡的效果越明显。然而，对于闭环控制系统，增益过大可能引起振荡。

分别取Ka=1.0，3.0和5.0，预想故障后发电机有功功率及无功功率响应曲线如图4所示。可见，适当提高PSS增益在增强系统阻尼的同时使无功反调作用也随之增强。建议在不明显减弱系统阻尼的情况下，适当选择PSS增益。

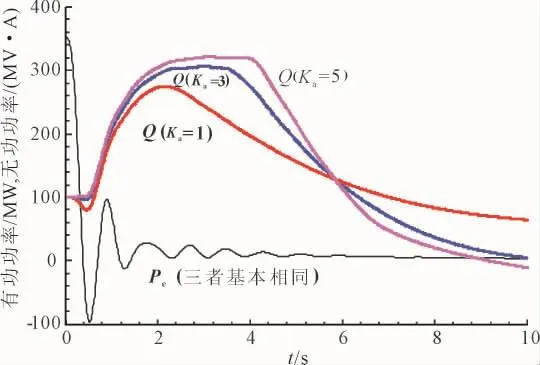
图4 不同PSS增益下发电机有功及无功功率曲线Fig.4 Generator power and reactive power responses during fast valving under different PSS gains

2.3 补偿系数对无功反调作用的影响

保持Tp不变，并分别取Kp=0.05（华中网同类型不同容量机组参数）、0.13（华中网同类型同容量机组参数）和0.6（初始参数），预想故障后发电机有功及无功功率响应曲线如图5所示。

图5 不同补偿系数时发电机有功及无功功率曲线Fig.5 Generator power and reactive power responses during fast valving under different compensation coefficients of PSS

可见，适当减少补偿系数有利于降低PSS无功反调作用，且对PSS阻尼效果影响不大。

2.4 隔直环节时间常数对无功反调作用的影响

隔直环节用于过滤输入信号中的直流分量，且使得t趋于∞时，经过该环节的输出为0。输入信号相同，隔直环节时间常数越小，同一时刻输出信号的幅值就越小。因此，隔直时间常数对无功反调也有一定影响。以Tw1为例，分别取Tw1=6.0（原参数）、2.0，预想故障后发电机有功及无功功率响应曲线如图6所示。

可见，减小隔直环节时间常数一定程度上有利于降低无功反调，且对PSS阻尼影响不大。进一步分析可知，采用双隔直环节，同样能起到有效抑制PSS无功反调的作用。

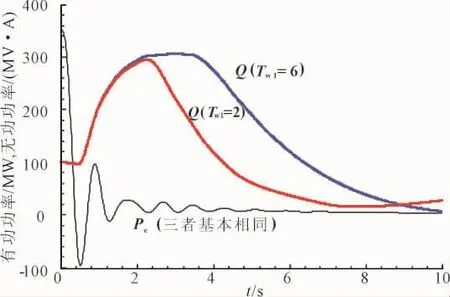
图6 不同隔直时间常数时发电机有功及无功功率曲线Fig.6 Generator power and reactive power responses during fast valving under different differential block time constants of PSS

2.5 其他参数对无功反调作用的影响

电磁功率积分时间常数Tp相当于式（4）中的发电机惯量M。当M较大时，令Tp略小于M可在降低无功反调作用的同时，减少相应惯性环节产生的相位滞后。

减小限幅参数Vsmax，相当于强行控制PSS输出限值，虽有利于降低无功反调作用，但同时对PSS提供阻尼效果有一定影响。

3 基于数字仿真方法整定加速功率型PSS参数的实现方案

该方法利用频域分析确定PSS安装地点，利用时域仿真软件和MATLAB软件计算相频特性，并校核整定方案的有效性。实现方案详述如下：

1）基于系统频域分析结果，根据系统负阻尼或弱阻尼模式的参与因子最大值，确定配置PSS的发电机组[15]。

2）计算发电机组在PSS退出条件下，其励磁系统相频特性曲线，记为曲线1。

3）根据曲线1相位滞后情况，整定计算双输入信号经过的各超前滞后环节时间常数[16]。

4）整定发电机转速偏差Δω信号及发电机电磁功率偏差ΔPe信号单独经过的惯性环节和隔直环节时间常数。

为有效补偿高频段励磁系统相位滞后，并防止PSS相位补偿后导致低频段相位超前，Δω通道隔直时间常数Tw1、Tw2初值取5～10 s；ΔPe通道Tw3、Tw4初值取3 s。

5）根据发电机惯量M计算补偿系数及电磁功率积分时间常数。考虑无功反调因素，建议取TP=k·M（其中k为略小于1的正数）。

6）将上述参数初值代入传递函数相应变量，利用MATLAB计算仅Δω信号工作时PSS传递函数的波特图，从中提取传递函数的相频特性曲线，记为曲线2。

7）根据曲线1和曲线2的相位角差异，对超前滞后环节时间常数进行微调。

一般地，针对特定频率fm或指定频段[f1，f2]曲线1与曲线2角度差θ12在10°～30°即可满足要求。

8）计算双输入信号同时工作时PSS传递函数的波特图，从中提取传递函数的相频特性曲线，记为曲线3；根据曲线1和曲线3的相位角差异，对隔直时间常数Tw3、Tw4进行微调。

由于线性定常系统为单输入单输出系统，为实现上述目的，需将双输入信号型PSS等值为单输入信号型PSS。由式（2）可知，不计发电机机械功率变化和阻尼系数时，ΔPe基本与-MsΔω同相位。因此，可通过增设一虚拟理想微分环节-Ms，将ΔPe信号转化为Δω信号。等值后的PSS传递函数如图7所示。

9）采用临界放大倍数法[17]获得PSS的临界增益Klim。PSS的最佳增益Kopt与PSS输入信号类型有关，对加速功率型PSS而言，建议取Kopt为临界增益的1/3。

图7 等值为单输入信号的PSS传递函数框图Fig.7 PSS transfer functions of equivalent single input signal model

4 仿真验证

依据上述实现方案，整定机组PSS参数如表1所示；发电机无PSS相位补偿时励磁系统的相频特性曲线、基于PSS原参数及改进参数的相频特性曲线如图8所示。

表1 机组PSS参数整定方案Tab.1 PSS parameters setting scheme of unit

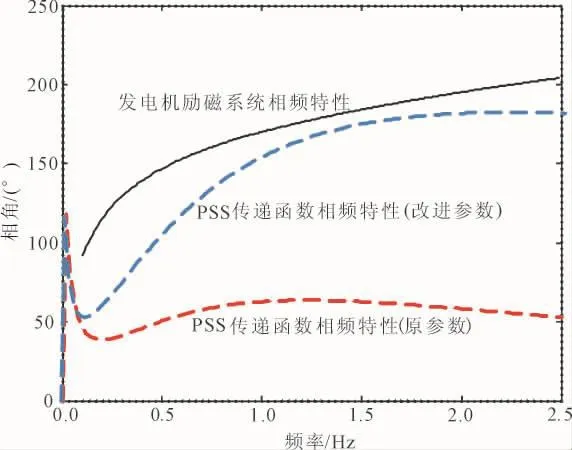
图8 发电机励磁系统相频特性曲线和PSS传递函数的相频特性曲线Fig.8 Phase-frequency characteristics of generator excitation system and PSS transfer functions

由图8可知，与原参数相比，改进的PSS可在0.3～2.0 Hz较宽频段内对励磁系统的相位滞后进行有效补偿。

仍以该实际电网机组汽门快关故障为例，不同PSS参数下发电机有功及无功功率响应曲线如图9所示。可见，改进的PSS参数不仅能够有效阻尼事故后系统功率振荡，而且，与原PSS参数相比，其无功反调程度大大降低。

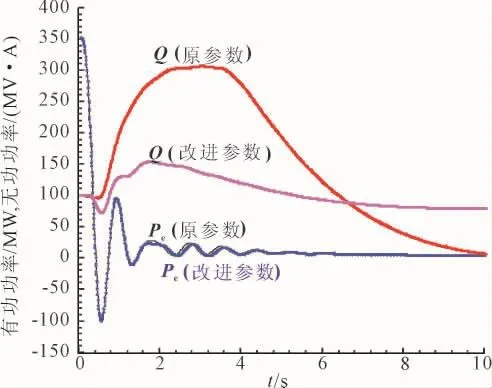
图9 不同PSS参数下发电机有功及无功功率曲线Fig.9 Generator power and reactive power responses during fast valving under different PSS parameters

5 结语

1）加速功率型PSS在参数不合理的情况下仍可能出现严重的无功反调现象；通过正确的参数整定，可在确保PSS提供有效阻尼的同时降低无功反调的影响。

2）减少补偿系数、隔直环节时间常数或增加隔直环节均能一定程度上降低无功反调作用，且对PSS阻尼效果影响不大。

3）在不明显降低PSS阻尼效果的前提下，减小PSS增益、控制限幅环节最大输出也有利于降低无功反调。

4）对加速功率型PSS而言，抑制反调最有效的方法是快速增减原动机出力时闭锁PSS的电磁功率信号通道。

[1] 余贻鑫，李鹏.大区电网弱互联对互联系统阻尼和动态稳定性的影响[J].中国电机工程学报，2005，25(11)：6-11.YU Yi-xin，LI Peng.The impact of weak internection of bulk power grids to damping and dynamic stability of power systems[J].Proceedings of the CSEE，2005，25(11)：6-11(in Chinese).

[2] 刘增煌，方思立.电力系统稳定器对电力系统动态稳定的作用及与其他控制方式的比较[J].电网技术，1998，22(3)：4-10.LIU Zeng-huang，FANG Si-li.The effect of PSS on power system dynamic stability and comparison with other control method[J].Power System Technology，1998，22(3)：4-10(in Chinese).

[3] 朱方，汤涌，张东霞，等.我国交流互联电网动态稳定性的研究及解决策略[J].电网技术，2004，28(15)：1-5.ZHU Fang，TANG Yong，ZHANG Dong-xia，et al.Study on dynamic stability problems of ac interconnected area power grids in china and their solutions[J].Power System Technology，2004，28(15)：1-5(in Chinese).

[4] IEEE Std421.5-2005 IEEE recommended practice for excitationsystemmodelsforpowersystemstabilitystudies[S].2005.

[5] 杨立强，王亮，赵红光，等.加速功率型电力系统稳定器的研制[J].电网技术，2004，28(23)：57-60.YANG Li-qiang，WANG Liang，ZHAO Hong-guang，et al.Development of power system stabilizer based on PSS2A model of IEEE[J].Power System Technology，2004，28(23)：57-60(in Chinese).

[6] 张仰飞，袁越，陈小虎，等.有功型PSS抑制低频振荡机理及反调特性[J].电力系统保护与控制，2010，38(3)：77-80.ZHANG Yang-fei，YUAN Yue，CHEN Xiao-hu，et al.Mechanism of active-power PSS low-frequency oscillation suppression and characteristic of anti-regulation[J].Power System Protection and Control，2010，38(3)：77-80(in Chinese).

[7] 竺士章，陈皓.汽轮发电机组电力系统稳定器的反调[J].浙江电力，2006，25(5)：9-11.ZHU Shi-zhang，CHEN Hao.Reverse action of power system stabilizer at turbine generator unit[J].Zhejiang Electric Power，2006，25(5)：9-11(in Chinese).

[8] 韩石成.小浪底水电厂电力系统稳定器无功反调现象及分析[J].水电能源科学，2007，25(2)：116-118.HAN Shi-cheng.Analysis of unit reactive power antiregulation at xiaolangdi hydropower plant[J].Water Resources and Power，2007，25(2)：116-118(in Chinese).

[9] 陈刚，程林，孙元章，等.基于小信号激励的多机PSS参数在线闭环整定[J].电力系统自动化，2011，35(5)：5-9.CHEN Gang，CHENG Lin，SUN Yuan-zhang，et al.Small signal excitation based online closed-loop setting method to multi-PSS parameters[J].Automation of Electric Power Systems，2011，35(5)：5-9(in Chinese).

[10]刘红超，雷宪章，李兴源，等.互联电力系统中PSS的全局协调优化[J].电网技术，2006，30(8)：1-6.LIU Hong-chao，LEI Xian-zhang，LI Xing-yuan，et al.Global coordinated optimization of PSSs in interconnected power systems[J].Power System Technology，2006，30(8)：1-6(in Chinese).

[11]吴峰，鲁晓帆，陈维荣，等.电力系统稳定器参数优化的研究[J].电力系统保护与控制，2010，38(5)：29-33.WU Feng，LU Xiao-fan，CHEN Wei-rong，et al.Research of parameter optimization of power system stabilizer[J].Power System Protection and Control，2010，38(5)：29-33(in Chinese).

[12]国家电网公司.Q/GDW 143-2206电力系统稳定器整定试验导则[S].北京：中国电力出版社，2002.

[13]杨立环，徐峰，胡华荣，等.电力系统稳定器PSS2A现场试验及参数整定[J].电力系统保护与控制，2010，38(1)：112-114.YANG Li-huan，XU Feng，HU Hua-rong，et al.Test and parameter-setting of power system stabilizer-PSS2A[J].Power System Protection and Control，2010，38(1)：112-114(in Chinese).

[14]竺士章，陈新琪，方思立，等.浙江电网电力系统稳定器PSS试验综述[J].浙江电力，2000(1)：1-4.ZHU Shi-zhang，CHEN Xin-qi，FANG Si-li，et al.Summary of tests of PSS in Zhejiang electric power system[J].Zhejiang Electric Power，2000(1)：1-4(in Chinese).

[15]倪以信，陈寿孙，张宝霖.动态电力系统理论和分析[M].北京：清华大学出版社，2002.

[16]方思立，朱方.电力系统稳定器的原理及其应用[M].北京：中国电力出版社，1996.

[17]竺士章.电力系统稳定器PSS放大倍数的整定[J].浙江电力,2002，21(6)：9-12.ZHU Shi-zhang.Setting of power system stabilizer gain[J].Zhejiang Electric Power,2002，21(6)：9-12(in Chinese).